Pythagoras Theorem
What is the Pythagoras theorem?
- The Pythagoras theorem states that ‘in a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares on the legs’.
- A right-angled triangle is a triangl e in which one angle is a right angle, that is its measure is 90 degrees.
- The side opposite to the right angle is called the hypotenuse.
- According to the Pythagoras theorem, the square of the length of the hypotenuse, is equal to the sum of the squares of the lengths of the other two sides.
Right-angled triangle
- So, if the lengths of the sides of a right-angled triangle are ‘a’, ‘b’ and ‘c’, where ‘c’ is the length of the hypotenuse, then c2 =a2 + b2
- This theorem holds true only in the case of a right triangle.
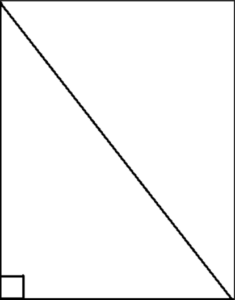
Proving Pythagoras Theorem:
Draw a square, with the length of all its sides equal to ‘c’ units.

Square of side length c
Construct a triangle with side ‘c’ as the hypotenuse, and the lengths of the sides as ‘a’ and b’ as shown below.
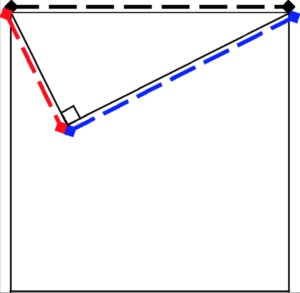
Right-angled triangle inside square
We need to prove that, c2 =a2 + b2
For this, draw a right-angled triangle on each side of the square, with hypotenuse as ‘c’, and the sides as ‘a’ units and ‘b’ units.
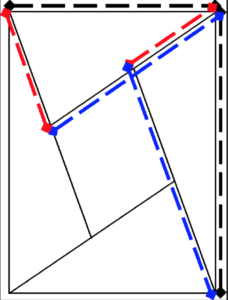
4 right-angled triangles inside square
Drawing all these triangles gives a square in the middle, with its side measuring ‘a – b ’.
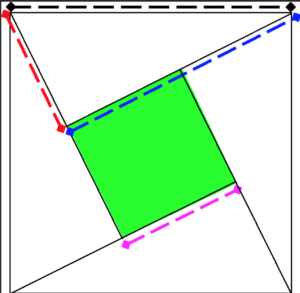
Square inside square
Let us now find the area of the larger square. There are two ways of doing it:
(i) Side multiplied by side
Area of the larger square = c × c = c2.
(ii) Sum of the areas of parts enclosed in the larger square
The larger square encloses four right-angled triangles and a small square in the centre. Adding the areas of all these figures will give the area of the larger square.
Each of the triangles has its height as ‘’ units and its base as ‘’ units. So, the total area of the 4 triangles = 4 (1/2 × a × b) = 2ab
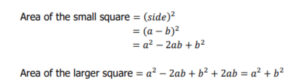
The expressions in (i) and (ii) are the area of the same square.
So, c2 =a2 + b2
Thus, the Pythagoras theorem is proved.
Solved Examples on Pythagorean Theorem:
Example 1. A right triangle has one leg measuring 5 cm and the other leg measuring 12 cm. Find the length of the hypotenuse.
Solution:
According to the Pythagorean Theorem, in a right triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two legs.
Let’s denote the lengths of the legs as a and b, and the length of the hypotenuse as c.
Given:
Leg a = 5 cm
Leg b = 12 cm
Using the Pythagorean Theorem:
c² = a² + b²
c² = 5² + 12²
c² = 25 + 144
c² = 169
To find the length of the hypotenuse (c), we take the square root of both sides:
c = √169
c = 13 cm
Therefore, the length of the hypotenuse in the right triangle is 13 cm.
Example 2. A ladder is leaning against a wall. The base of the ladder is 6 feet away from the wall, and the ladder reaches a height of 8 feet on the wall. What is the length of the ladder?
Solution:
In this scenario, the ladder, the wall, and the ground form a right triangle. Let’s denote the length of the ladder as c, the distance between the base of the ladder and the wall as a, and the height of the ladder on the wall as b.
Given:
a = 6 feet
b = 8 feet
Using the Pythagorean Theorem:
c² = a² + b²
c² = 6² + 8²
c² = 36 + 64
c² = 100
To find the length of the ladder (c), we take the square root of both sides:
c = √100
c = 10 feet
Therefore, the length of the ladder is 10 feet.
Frequently Asked Questions on Pythagorean Theorem:
- What is the Pythagorean Theorem?
Answer: The Pythagorean Theorem states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides.
- How is the Pythagorean Theorem represented mathematically?
Answer: The Pythagorean Theorem can be expressed as the equation: a² + b² = c², where ‘a’ and ‘b’ are the lengths of the two legs of the right triangle, and ‘c’ is the length of the hypotenuse.
- When can the Pythagorean Theorem be applied?
Answer: The Pythagorean Theorem can only be applied to right triangles, which are triangles that have one angle measuring 90 degrees (a right angle).
- What can the Pythagorean Theorem be used to find?
Answer: The Pythagorean Theorem can be used to find the length of an unknown side in a right triangle, given the lengths of the other two sides. It is commonly used to solve problems involving distances, lengths, areas, and determining if a triangle is a right triangle.
- Can the Pythagorean Theorem be used in non-right triangles?
Answer: No, the Pythagorean Theorem is specifically applicable only to right triangles. For other types of triangles, different theorems and formulas must be used.
- Who discovered the Pythagorean Theorem?
Answer: The Pythagorean Theorem is named after the ancient Greek mathematician Pythagoras, who is credited with its discovery. However, evidence suggests that the theorem was known and used by earlier civilizations as well.
- What are some real-life applications of the Pythagorean Theorem?
Answer: The Pythagorean Theorem is applied in various fields such as architecture, engineering, construction, surveying, navigation, and physics. It can be used to calculate distances, determine the lengths of diagonals, solve problems involving right triangles, and much more.

