What is the Area of a square?
A square is a two-dimensional geometric shape with four equal sides and four right angles. The area of a square refers to the measure of the region enclosed within its boundaries. It is a fundamental concept in geometry and is calculated using a simple formula.
The Area of a square is equal to the square of the length of its side. Consider a square whose sides are of length ‘S’.
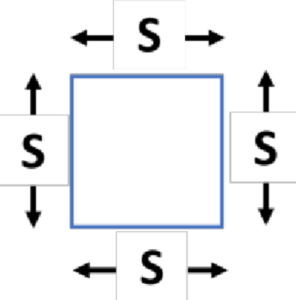
Thus, the area of the square = s × s= s2.That is, the area of a square is (side of the square)2.
For example,
Consider a square whose sides are 12 cm each. Then, the area of this square = side2
= 122
= 144
Thus, the area of the square is 144.
The area of a square is always expressed in square units, such as square centimetres (cm²), square inches (in²), or square meters (m²). For example, if the side length of a square is given in centimetres, the resulting area will be in square centimetres.
Properties of Square and its area:
- All sides of a square are equal in length.
- The opposite sides of a square are parallel and congruent.
- The diagonals of a square are congruent and bisect each other at right angles.
- The area of a square is always non-negative, as it represents a physical area.
The area of a square is useful in various real-life applications, such as calculating the floor area of a square-shaped room, determining the amount of material required to cover a square surface, or estimating the space occupied by a square plot of land.
It is important to note that the area of a square is solely dependent on its side length. Therefore, if the side length is known, the area can be easily calculated using the formula mentioned above.
Solved Examples on Area of Square:
Example 1. Find the area of a square with a side length of 6 units.
Solution:
The formula for the area of a square is given by: Area = side length².
Substituting the given side length:
Area = 6²
Area = 36 square units
Therefore, the area of the square is 36 square units.
Example 2. If the diagonal of a square is 10 units, find its area.
Solution:
In a square, the diagonal divides the square into two congruent right triangles. The length of each side of the square can be found using the Pythagorean Theorem.
Let the side length of the square be “s”. According to the Pythagorean Theorem: diagonal² = side length² + side length².
Substituting the given diagonal length:
10² = s² + s²
100 = 2s²
s² = 50
s ≈ 7.07 (approximated to two decimal places)
Now that we have the side length, we can calculate the area:
Area = side length²
Area = (7.07)²
Area ≈ 49.99 square units (approximated to two decimal places)
Therefore, the area of the square is approximately 49.99 square units.
Example 3. The area of a square is 64 square centimetres. Find the length of its side.
Solution:
To find the length of the side of a square when the area is given, we can use the formula: side length = √(Area).
Substituting the given area:
side length = √64
side length = 8 centimetres
Therefore, the length of the side of the square is 8 centimetres.
Frequently Asked Questions on Area of Square:
- What is the area of a square?
Answer: The area of a square is the measure of the region enclosed within its boundaries. It represents the amount of space occupied by the square and is expressed in square units.
- How is the area of a square calculated?
Answer: The area of a square is calculated by multiplying the length of one side by itself. The formula for the area of a square is: Area = side length².
- What are the units used for measuring the area of a square?
Answer: The area of a square is typically measured in square units, such as square centimetres (cm²), square inches (in²), or square meters (m²), depending on the system of measurement used.
- Can the area of a square be calculated if only the diagonal is given?
Answer: No, the area of a square cannot be directly determined with only the diagonal length. The diagonal length alone does not provide enough information to calculate the side length of the square, which is required to find the area.
- What is the relationship between the area and the side length of a square?
Answer: The area of a square is directly proportional to the square of its side length. This means that if the side length is doubled, the area will be quadrupled, and if the side length is halved, the area will be reduced to one-fourth.
- How is the area of a square related to the perimeter?
Answer: The area of a square and its perimeter are independent of each other. While the area is a measure of the enclosed space, the perimeter is the total length of the square’s boundary. They have different formulas and represent different aspects of the square.
- Can the area of a square be negative?
Answer: No, the area of a square is always non-negative. It represents a physical quantity, and a negative area does not have any practical meaning.
- Can the area of a square be zero?
Answer: Yes, the area of a square can be zero if the side length is zero. In this case, the square degenerates into a single point.



