Important Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Important Questions for Class 10 Maths Chapter 8 Introduction to Trigonometry

Introduction to Trigonometry Class 10 Important Questions Very Short Answer (1 Mark)

Question 1.
If tan θ + cot θ = 5, find the value of tan2θ + cotθ. (2012)
Solution:
tan θ + cot θ = 5 … [Given
tan²θ + cot²θ + 2 tan θ cot θ = 25 … [Squaring both sides
tan²θ + cot²θ + 2 = 25
∴ tan²θ + cot²θ = 23

Question 2.
If sec 2A = cosec (A – 27°) where 2A is an acute angle, find the measure of ∠A. (2012, 2017D)
Solution:
sec 2A = cosec (A – 27°)
cosec(90° – 2A) = cosec(A – 27°) …[∵ sec θ = cosec (90° – θ)
90° – 2A = A – 27°
90° + 27° = 2A + A
⇒ 3A = 117°
∴ ∠A = \(\frac{117^{\circ}}{3}\) = 39°

Question 3.
If tan α = \(\sqrt{3}\) and tan β = \(\frac{1}{\sqrt{3}}\),0 < α, β < 90°, find the value of cot (α + β). (2012)
Solution:
tan α = \(\sqrt{3}\) = tan 60° …(i)
tan β = \(\frac{1}{\sqrt{3}}\) = tan 30° …(ii)
Solving (i) & (ii), α = 60° and β = 30°
∴ cot (α + β) = cot (60° + 30°) = cot 90° = 0

Question 4.
If sin θ – cos θ = 0, find the value of sin4 θ + cos4 θ. (2012, 2017D)
Solution:
sin θ – cos θ = 0 = sin θ = cos θ
⇒ \(\frac{\sin \theta}{\cos \theta}\) = 1 ⇒ tan θ = 1 ⇒ θ = 45°
Now, sin⁴θ + cos⁴θ
= sin⁴ 45° + cos⁴ 45°
= \(\left(\frac{1}{\sqrt{2}}\right)^{4}+\left(\frac{1}{\sqrt{2}}\right)^{4}=\frac{1}{4}+\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)

Question 5.
If sec θ + tan θ = 7, then evaluate sec θ – tan θ. (2017OD)
Solution:
We know that,
sec²θ – tan²θ = 1
(sec θ + tan θ) (sec θ – tan θ) = 1
(7) (sec θ – tan θ) = 1 …[sec θ + tan θ = 7; (Given)
∴ sec θ – tan θ = \(\frac{1}{7}\)

Question 6.
Evaluate: 10. \(\frac{1-\cot ^{2} 45^{\circ}}{1+\sin ^{2} 90^{\circ}}\). (2014)
Solution:

Question 7.
If cosec θ = \(\frac{5}{4}\), find the value of cot θ. (2014)
Solution:
We know that, cot²θ = cosec²θ – 1
= \(\left(\frac{5}{4}\right)^{2}\) – 1 ⇒ \(\frac{25}{16}\) – 1 ⇒ \(\frac{25-16}{16}\)
coť²θ = \(\frac{9}{16}\) i cot θ = \(\frac{3}{4}\)

Question 8.
If θ = 45°, then what is the value of 2 sec²θ + 3 cosec²θ ? (2014)
Solution:
2 sec²θ + 3 cosec²θ = 2 sec² 45° + 3 cosec² 45°
= 2(\(\sqrt{2}\))² + 3 (\(\sqrt{2}\))² = 4 + 6 = 10

Question 9.
If \(\sqrt{3}\) sin θ = cos θ, find the value of \(\frac{3 \cos ^{2} \theta+2 \cos \theta}{3 \cos \theta+2}\). (2015)
Solution:
\(\sqrt{3}\) sin θ = cos θ … [Given

Question 10.
Evaluate: sin² 19° + sin⁷71°. (2015)
Solution:
sin² 19° + sin² 71°
= sin²19° + sin² (90° – 19°)…[∵ sin(90° – θ) = cos θ
= sin² 19° + cos² 19° = 1 …[∵ sin² θ + cos² θ = 1

Question 11.
What happens to value of cos when increases from 0° to 90°? (2015)
Solution:
cos 0° = 1, cos 90° = 0
When θ increases from 0° to 90°, the value of cos θ decreases from 1 to 0.

Question 12.
If tan θ = \(\frac{a}{x}\), find the value of \(\frac{x}{\sqrt{a^{2}+x^{2}}}\). (2013)
Solution:

Question 13.
If in a right angled ∆ABC, tan B = \(\frac{12}{5}\), then find sin B. (2014)
Solution:
1st method:
tan B = \(\frac{12}{5}\) ∴ cot B = \(\frac{5}{12}\)
cosec² B = 1 + cot² B
= 1 + \([\left(\frac{5}{12}\right)^{2}/latex] = 1 + \[\]\)
= \(\frac{144+25}{144}=\frac{169}{144}\)
cosec B = \(\frac{13}{12}\) ∴ sin B = \(\frac{12}{13}\)
2nd method:

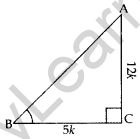
tan B = \(\frac{12}{5}\)
tan B = \(\frac{AC}{BC}\)
Let AC = 12k, BC = 5k
In rt. ∆ACB,
AB² = AC² + BC² …[Pythagoras theorem
AB² = (12k)² + (5k)²
AB² = 144k² + 25k²2 = 169k²
AB = 13k
∴ sin B = \(\frac{\mathrm{AC}}{\mathrm{AB}}=\frac{12 \mathrm{k}}{13 \mathrm{k}}=\frac{12}{13}\)

Question 14.
If ∆ABC is right angled at B, what is the value of sin (A + C). (2015)
Solution:

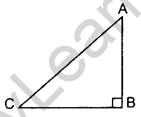
∠B = 90° …[Given
∠A + ∠B + ∠C = 180° …[Angle sum property of a ∆
∠A + ∠C + 90° = 180°
∠A + ∠C = 90°
∴ sin (A + C) = sin 90° = 1 …(taking sin both side

Introduction to Trigonometry Class 10 Important Questions Short Answer-I (2 Marks)

Question 15.
Evaluate: tan 15° . tan 25° , tan 60° . tan 65° . tan 75° – tan 30°. (2013)
Solution:
tan 15°. tan 25°, tan 60°. tan 65°. tan 75° – tan 30°
= tan(90° – 75°) tan(90° – 65°). \(\sqrt{3}\) . tan 65°. tan 75° – \(\frac{1}{\sqrt{3}}\)

Question 16.
Express cot 75° + cosec 75° in terms of trigonometric ratios of angles between 0° and 30°. (2013)
Solution:
cot 75° + cosec 75°
= cot(90° – 15°) + cosec(90° – 15°)
= tan 15° + sec 15° …[cot(90°-A) = tan A
cosec(90° – A) = sec A

Question 17.
If cos (A + B) = 0 and sin (A – B) = 3, then find the value of A and B where A and B are acute angles. (2012)
Solution:

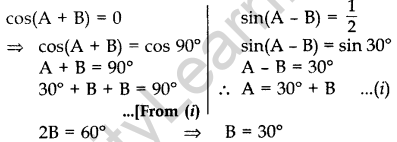
Putting the value of B in (i), we get
⇒ A = 30° + 30° = 60°
∴ A = 60°, B = 30°

Question 18.
If A, B and C are the interior angles of a ∆ABC, show that sin \(\left(\frac{A+B}{2}\right)\) = cos\(\left(\frac{c}{2}\right)\). (2012)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° …(Angle sum property of ∆
∠A + ∠B = 180° – ∠C

Question 19.
If x = p sec θ + q tan θ and y = p tan θ + q sec θ, then prove that x² – y² = p² – q². (2014)
Solution:
L.H.S. = x² – y²
= (p sec θ + q tan θ)² – (p tan θ + q sec θ)²
= p² sec θ + q² tan² θ + 2 pq sec ² tan ² -(p² tan² θ + q² sec² θ + 2pq sec θ tan θ)
= p² sec θ + 2 tan² θ + 2pq sec θ tan θ – p² tan² θ – q² sec θ – 2pq sec θ tan θ
= p²(sec² θ – tan² θ) – q²(sec?² θ – tan² θ) =
= p² – q² …[sec² θ – tan² θ = 1
= R.H.S.

Question 20.
Prove the following identity: (2015)
\(\frac{\sin ^{3} \theta+\cos ^{3} \theta}{\sin \theta+\cos \theta}\) = 1 – sin θ . cos θ
Solution:

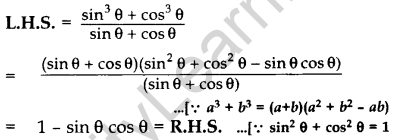
Question 21.
Simplify: \(\frac{1+\tan ^{2} A}{1+\cot ^{2} A}\). (2014)
Solution:

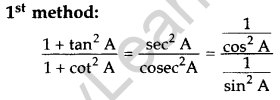
Question 22.
If x = a cos θ – b sin θ and y = a sin θ + b cos θ, then prove that a² + b² = x² + y². (2015)
Solution:
R.H.S. = x² + y²
= (a cos θ – b sin θ)² + (a sin θ + b cos θ)²
= a²cos² θ + b² sin² θ – 2ab cos θ sin θ + a² sin² θ + b² cos² θ + 2ab sin θ cos θ
= a²(cos² θ + sin²θ) + b² (sin² θ + cos² θ)
= a² + b² = L.H.S. …[∵ cos² θ + sin² θ = 1

Introduction to Trigonometry Class 10 Important Questions Short Answer – II (3 Marks)

Question 23.
Given 2 cos 3θ = \(\sqrt{3}\), find the value of θ. (2014)
Solution:
2 cos 3θ = \(\sqrt{3}\) …[Given
cos 3θ = \(\frac{\sqrt{3}}{2}\) ⇒ cos 3θ = cos 30°
30 = 30° ∴ θ = 10°

Question 24.
If cos x = cos 40° . sin 50° + sin 40°. cos 50°, then find the value of x. (2014)
Solution:
cos x = cos 40° sin 50° + sin 40° cos 50°
cos x = cos 40° sin(90° – 40°) + sin 40°.cos(90° – 40°)
cos x = cos² 40° + sin² 40°
cos x = 1 …[∵ cos² A + sin² A = 1
cos x = cos 0° ⇒ x = 0°

Question 25.
If sin θ = \(\frac{1}{2}\), then show that 3 cos θ – 4 cos³ θ = 0. (2014)
Solution:
sin θ = \(\frac{1}{2}\)
sin θ = sin 30° ⇒ θ = 30°
L.H.S = 3 cos θ – 4 cos³ θ
= 3 cos 30° – 4 cos³(30°)

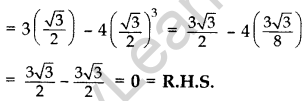
Question 26.
If 5 sin θ = 4, prove that \(\frac{1}{\cos \theta}+\frac{1}{\cot \theta}\) = 3 (2013
Solution:
Given: 5 sin θ = 4

Question 27.
Evaluate: sec 41°. sin 49° + cos 29°.cosec 61° 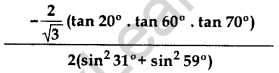(2012)
Solution:

Question 28.
Evaluate: (2012, 2017D)

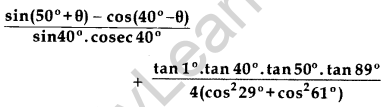
Solution:

Question 29.
In figure, ∆PQR right angled at Q, PQ = 6 cm and PR = 12 cm. Determine ∠QPR and ∠PRQ. (2013)

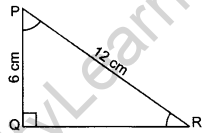
Solution:
In rt. ∆PQR,
PQ² + QR² = PR² …[By Pythogoras’ theorem

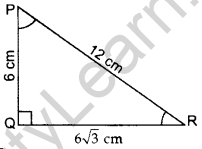
(6)² + QR² = (12)²
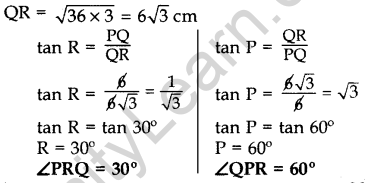
QR² = 144 – 36
QR² = 108

Question 30.
Find the value of: (2013)

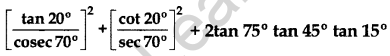
Solution:

Question 31.
Prove that: \(\frac{\sin ^{2} 63^{\circ}+\sin ^{2} 27^{\circ}}{\sec ^{2} 20^{\circ}-\cot ^{2} 70^{\circ}}\) + 2 sin 36° sin 42° sec 48° sec 54° (2017OD)
Solution:

Question 32.
If sin θ = \(\frac{12}{13}\), 0° <0 < 90°, find the value of: \(\frac{\sin ^{2} \theta-\cos ^{2} \theta}{2 \sin \theta \cdot \cos \theta} \times \frac{1}{\tan ^{2} \theta}\) (2015)
Solution:

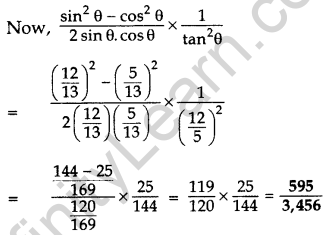
Question 33.
Prove that: (2012)

Solution:

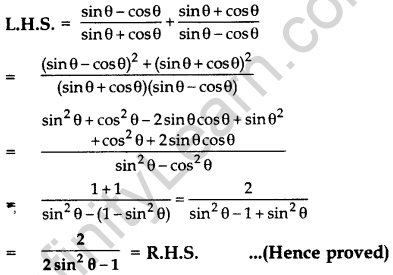
Question 34.
Prove that: \(\frac{\tan \theta+\sec \theta-1}{\tan \theta-\sec \theta+1}=\frac{1+\sin \theta}{\cos \theta}\) (2012, 2017D)
Solution:

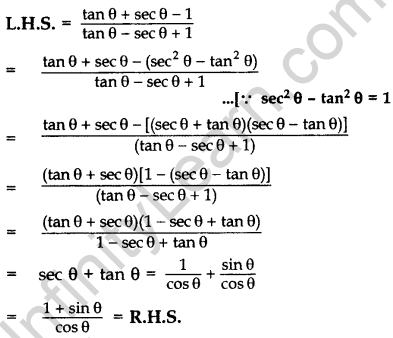
Question 35.
If tan θ = \(\frac{a}{b}\), prove that \(\frac{a \sin \theta-b \cos \theta}{a \sin \theta+b \cos \theta}=\frac{a^{2}-b^{2}}{a^{2}+b^{2}}\) (2013)
Solution:

Question 36.
Prove the identity: (sec A – cos A). (cot A + tan A) = tan A . sec A. (2014)
Solution:
L.H.S.= (sec A – cos A) (cot A + tan A)

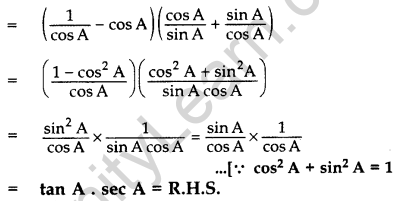
Question 37.
If sec θ + tan θ = p, prove that sin θ = \(\frac{p^{2}-1}{p^{2}+1}\) (2015)
Solution:

Question 38.
Prove that: \(\frac{\sin \theta-2 \sin ^{3} \theta}{2 \cos ^{3} \theta-\cos \theta}\) = tan θ (2015)
Solution:

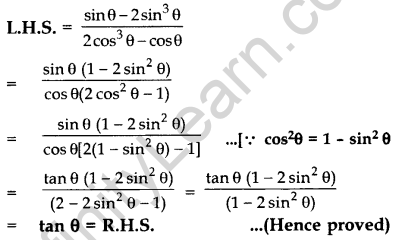
Question 39.
Prove that: \(\frac{\sin \theta}{1+\cos \theta}+\frac{1+\cos \theta}{\sin \theta}\) = 2 cosec θ (2017OD)
Solution:

Introduction to Trigonometry Class 10 Important Questions Long Answer (4 Marks)

Question 40.
In an acute angled triangle ABC, if sin (A + B – C) = \(\frac{1}{2}\) and cos (B + C – A) = \(\frac{1}{\sqrt{2}}\), find ∠A, ∠B and ∠C. (2012)
Solution:

Putting the values of A and B in (iii), we get
67.5° + B + 75o = 180°
B = 180° – 67.5° – 75o = 37.5°
∴ ∠A = 67.5°, ∠B = 37.5° and ∠C = 75°

Question 41.
Evaluate: (2013)

Solution:

Question 42.
Evaluate the following: (2015)

Solution:

Question 43.
If θ = 30°, verify the following: (2014)
(i) cos 3θ = 4 cos³ θ – 3 cos θ
(ii) sin 3θ = 3 sin θ – 4 sin³θ
Solution:

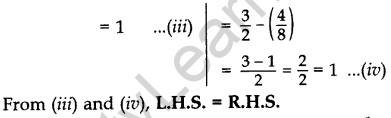
Question 44.
If tan (A + B) = \(\sqrt{3}\) and tan (A – B) = \(\frac{1}{\sqrt{3}}\) where 0 < A + B < 90°, A > B, find A and B. Also calculate: tan A. sin (A + B) + cos A. tan (A – B). (2015)
Solution:

Question 45.
Find the value of cos 60° geometrically. Hence find cosec 60°. (2012, 2017D)
Solution:

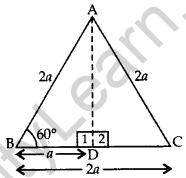
Let ∆ABC be an equilateral ∆.
Let each side of triangle be 2a.
Since each angle in an equilateral ∆ is 60°
∴ ∠A = ∠B = ∠C = 60°
Draw AD ⊥ BC
In ∆ADB and A∆ADC,
AB = AC … [Each = 2a
AD = AD …[Common
∠1 -∠2 … [Each 90°
∴ ∆ADB = ∆ADC …[RHS congruency rule
BD = DC = \(\frac{2 a}{2}\) = a
In rt. ∆ADB, cos 60° = \(\frac{\mathrm{BD}}{\mathrm{AB}}=\frac{a}{2 a}=\frac{1}{2}\)

Question 46.
If tan(20° – 3α) = cot(5α – 20°), then find the value of α and hence evaluate: sin α. sec α . tan α – cosec α . cos α . cot α. (2014)
Solution:
tan(20° – 3α) = cot(5α – 20°)
tan(20° – 3α) = tan[90° – (5α – 20°)] …[∵ cot θ = tan(90° – θ)] ∴ 20° – 3α = 90° – 5α + 20°
⇒ -3α + 5α = 90° + 20° – 20°
⇒ 2α = 90° ⇒ α = 45°
Now, sin α . sec α tan α – cosec α . cos α . cot α
= sin 45°. sec 45° tan 45° – cosec 45°. cos 45° cot 45°
= \(\frac{1}{\sqrt{2}} \times \sqrt{2} \times 1-\sqrt{2} \times \frac{1}{\sqrt{2}} \times 1=1-1=0\)

Question 47.
If \(\frac{x}{a}\)cosθ + \(\frac{y}{b}\)sinθ = 1 and \(\frac{x}{a}\)sinθ – \(\frac{y}{b}\) cosθ = 1, prove that event \(\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}\) = 2. (2012, 2017D)
Solution:

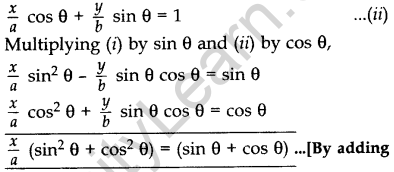
Question 48.
If sin θ = \(\frac{c}{\sqrt{c^{2}+d^{2}}}\) and d > 0, find the values of cos θ and tan θ. (2013)
Solution:

Question 49.
If cot B = \(\frac{12}{5}\), prove that tan²B – sin²B = sin⁴ B . sec² B. (2013)
Solution:
cot B = \(\frac{12}{5}\) :: \(\frac{A B}{B C}=\frac{12}{5}\)

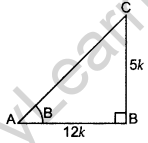
AB = 12k, BC = 5k
In rt. ∆ABC, …[By Pythagoras’ theorem
AC² = AB² + BC²
AC² = (12k)² + (5k)²
AC² = 144k² + 25k²
AC² = 169k²
AC = +13k …[∵ Hypotenuse cannot be -ve

Question 50.
If \(\sqrt{3}\) cot²θ – 4 cot θ + \(\sqrt{3}\) = 0, then find the value of cot² θ + tan²θ. (2013)
Solution:

Question 51.
Prove that b²x² – a²y² = a²b², if: (2014)
(i) x = a sec θ, y = b tan θ
(ii) x = a cosec θ, y = b cot θ
Solution:
(i) L.H.S. = b²x² – a²y²
= b²(a sec θ)² – a²(b tan θ)²
= b²a² sec θ – a²b² tan²θ
= b²a²(sec² θ – tan² θ)
= b²a²(1) …[∵ sec²θ – tan² θ = 1
= a²b² = R.H.S.

(ii) L.H.S. = b²x² – a²y²
= b²(a cosec θ)² – a²(b cot θ)²
= b²a² cosec² θ – a²b² cot² θ
= b²a²(cosec²θ – cot² θ)
= b²a² (1) ..[∵ cosec² θ – cot² θ = 1
= a²b²= R.H.S.

Question 52.
If sec θ – tan θ = x, show that sec θ + tan θ = \(\frac{1}{x}\) and hence find the values of cos θ and sin θ. (2015)
Solution:

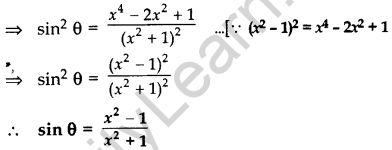
Question 53.
If cosec θ + cot θ = p, then prove that cos θ = \(\frac{p^{2}-1}{p^{2}+1}\). (2012)
Solution:
cosec θ + cot θ = p

Question 54.
If tan θ + sin θ = p; tan θ – sin θ = q; prove that p² – q² = \(4 \sqrt{p q}\). (2012)
Solution:
L.H.S. = p² – q²
= (tan θ + sin θ)² – (tan θ – sin θ)²
= (tan²θ + sin²θ + 2.tanθ.sinθ) – (tan²θ + sin²θ – 2tan θ sin θ)
= 2 tan θ sin θ+ 2 tan θ sin θ
= 4 tan θ sin θ …(i)

Question 55.
If sin θ + cos θ = m and sec θ + cosec θ = n, then prove that n(m² – 1) = 2m. (2013)
Solution:
m² – 1 = (sin θ + cos θ)² – 1
= sin² θ + cos²θ + 2 sin θ cos θ – 1
= 1 + 2 sin θ cos θ – 1
= 2 sin θ cos θ …[sin² θ + cos² θ = 1
L.H.S. = n(m² – 1)
= (sec θ + cosec θ) 2 sin θ cos θ

Question 56.
Prove that: 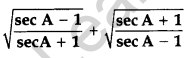= 2 cosec A (2012)
Solution:

Question 57.
In ∆ABC, show that sin² \(\frac{\mathbf{A}}{2}\) + sin² \(\frac{\mathbf{B}+\mathbf{C}}{\mathbf{2}}\) = 1. (2013)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° … [Sum of the angles of ∆
∠B + ∠C = 180° – ∠A

Question 58.
Find the value of: (2013)

Solution:

Question 59.
Prove that: (sin θ + cos θ + 1). (sin θ – 1 + cos θ) . sec θ . cosec θ = 2 (2014)
Solution:
L.H.S. = (sin θ + cos θ + 1) (sin θ – 1 + cos θ) . sec θ cosec θ
= [(sin θ + cos θ) + 1] [(sin θ + cos θ) – 1] . sec θ cosec θ
= [(sin θ + cos θ)² – (1)²] sec θ cosec θ …[∵ (a + b)(a – b) = a² – b²
= (sin² θ + cos²θ + 2 sin θ cos θ – 1]. sec θ cosec θ
= (1 + 2 sin θ cos θ – 1). sec θ cosecθ …[∵ sin²θ + cos²θ = 1
= (2 sin θ cos θ). \(\frac{1}{\cos \theta} \cdot \frac{1}{\sin \theta}\)
= 2 = R.H.S. …(Hence proved)

Question 60.
Prove that: (2014)

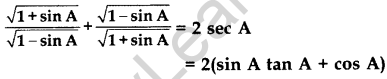
Solution:

Question 61.
Prove that: (1 + cot A + tan A). (sin A – cos A) = \(\frac{\sec ^{3} A-\csc ^{3} A}{\sec ^{2} A \cdot \csc ^{2} A}\) (2015)
Solution:

Question 62.
Prove the identity: (2015)

Solution:

Question 63.
Prove the following trigonometric identities: sin A (1 + tan A) + cos A (1 + cot A) = sec A + cosec A. (2015)
Solution:
L.H.S.
= sin A (1 + tan A) + cos A (1 + cot A)

Question 64.
Prove that: (cot A + sec B)² – (tan B – cosec A)² = 2(cot A . sec B + tan B. cosec A) (2014)
Solution:
L.H.S.
= (cot A + sec B)² – (tan B – cosec A)²
= cot² A + sec² B + 2 cot A sec B – (tan² B + cosec² A – 2 tan B cosec A)
= cot² A + sec² B + 2 cot A sec B – tan² B – cosec² A + 2 tan B cosec A
= (sec² B – tan² B) – (cosec² A – cot² A) + 2(cot A sec B + tan B cosec A)
= 1 – 1 + 2(cot A sec B + tan B cosec A) … [∵ sec²B – tan² B = 1
cosec²A – cot² A = 1
= 2(cot A . sec B + tan B . cosec A) = R.H.S.

Question 65.
If x = r sin A cos C, y = r sin A sin C and z = r cos A, then prove that x² + y² + z² = r². (2017OD)
Solution:
x = r sin A cos C; y = r sin A sin C; z = r cos A
Squaring and adding,
L.H.S. x² + y² + z² = 2 sin² A cos²C + r² sin² A sin² C + r² cos² A
= r² sin² A(cos² C + sin² C) + r² cos² A
= r² sin² A + r² cos² A … [cos²θ + sin²θ = 1
= r² (sin² A + cos² A) = r² = R.H.S.

Question 66.
Prove that: (2017OD)

Solution:

Question 67.
In the adjoining figure, ABCD is a rectanlge with breadth BC = 7 cm and ∠CAB = 30°. Find the length of side AB of the rectangle and length of diagonal AC. If the ∠CAB = 60°, then what is the size of the side AB of the rectangle. [Use \(\sqrt{3}\) = 1.73 and \(\sqrt{2}\) = 1.41, if required) (2014OD)

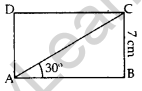
Solution: