Table of Contents
CBSE Class 10 Previous Year Question Papers
Get CBSE Previous Year Question Papers for Class 10 Maths on Infinity Learn for free.
Maths SA2 Outside Delhi – 2014
Time allowed: 3 hours Maximum marks: 90
GENERAL INSTRUCTIONS:
- All questions are compulsory.
- The Question Taper consists of 31 questions divided into four Sections A, B. C. and D.
- Section A contains 4 questions of 1 mark each. Section B contains 6 questions of 2 marks each, Section C contains 10 questions of 3 marks each and Section D contains 11 questions of 4 marks each.
- Use of calculators is not permitted.
SET I
SECTION A
Questions number 1 to 4 carry 1 mark each.
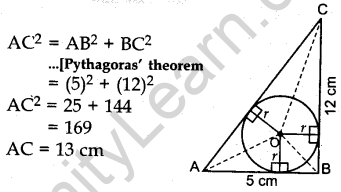
Question.1 In a right triangle ABC, right-angled at B, BC = 12 cm and AB = 5 cm. Calculate the radius of the circle inscribed in the triangle (in cm).
Solution.

Question.2 In a family of 3 children calculate the probability of having at least one boy.
Solution.
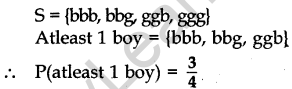
Question.3 ABCD is a rectangle whose three vertices are B(4, 0), C(4, 3) and D(0, 3). Calculate the length of one of its diagonals.
Solution.

Question.4 A chord of a circle of radius 10 cm subtends a right angle at its centre. Calculate the length of the chord (in cm).
Solution.

SECTION B
Questions number 5 to 10 carry 2 marks each.
Question.5 Find the values of p for which the quadratic equation 4x2 + px + 3 = 0 has equal roots.
Solution.
Question.6 Find the number of natural numbers between 101 and 999 which are divisible by both 2 and 5.
Solution.
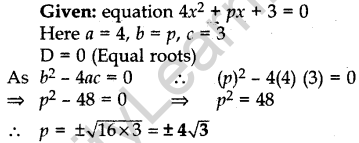
Question.7 In Figure 1, common tangents AB and CD to the two circles with centres O1 and O2 intersect at E. Prove that AB = CD.
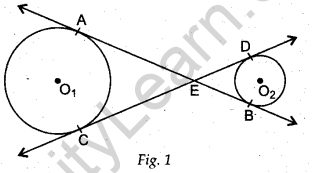
Solution.
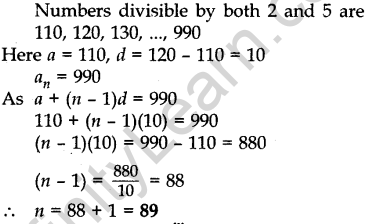
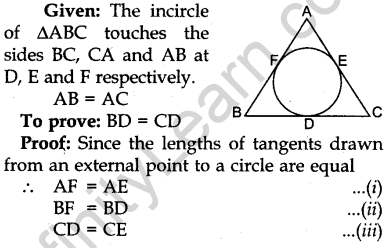
Question.8 The incircle of an isosceles triangle ABC, in which AB = AC, touches the sides BC, CA and AB at D, E and F respectively. Prove that BD = DC.
Solution.
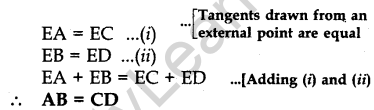
Question.9 Two different dice are tossed together. Find the probability
(i) that the number on each die is even.
(ii) that the sum of numbers appearing on the two dice is 5.
Solution.

Question.10 If the total surface area of a solid hemisphere is 462 cm2, find its volume. [Take π=22/7]
Solution.

SECTION C
Questions number 11 to 20 carry 3 marks each.
Question.11 Solve for
![]()
Solution.
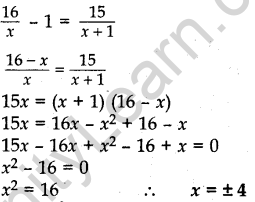
Question.12 The sum of the 5th and the 9th terms of an AP is 30. If its 25th term is three times its 8th term, find the AP.
Solution.
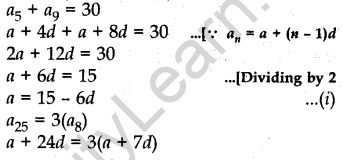
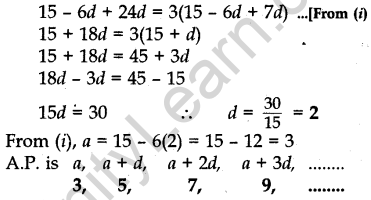
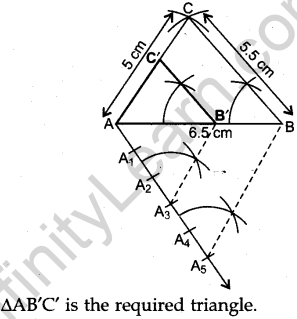
Question.13 Construct a triangle with sides 5 cm, 5.5 cm and 6.5 cm. Now construct another triangle,
whose sides are 3/5 times the corresponding sides of the given triangle.
Solution.
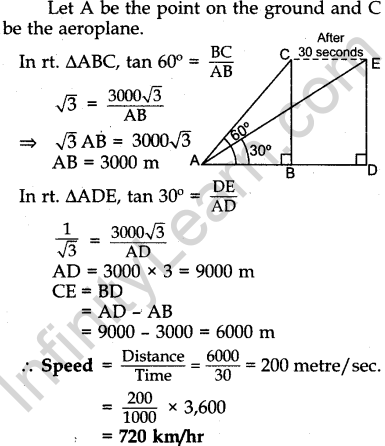
Question.14 The angle of elevation of an aeroplane from a point on the ground is 60°. After a flight of 30 seconds the angle of elevation becomes 30°. If the aeroplane is flying at a constant height of 3000 √3 m, find the speed of the aeroplane.
Solution.
Question.15 If the point P(k – 1, 2) is equidistant from the points A(3, k) and B(k, 5), find the values of k.
Solution.
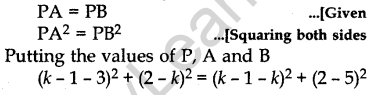

Question.16. Find the ratio in which the line segment joining the points A(3, -3) and B(-2, 7) is divided by x-axis. Also find the coordinates of the point of division.
Solution.

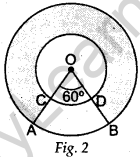
Question.17 In Figure 2, two concentric circles with centre O, have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. [Use π = 22/7 ]
Solution.


Question.18 The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the
volume of the wood left. [Use π = 22/7 ]
Solution.

Question.19 Water in a canal, 6 m wide and 1.5 m deep, is flowing at a speed of 4 km/h. How much area will it irrigate in 10 minutes, if 8 cm of standing water is needed for irrigation?
Solution.

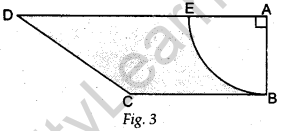
Question.20 In Figure 3, ABCD is a trapezium of area 24.5 sq. cm. In it, AD || BC, ∠DAB = 90°, AD = 10 cm and BC = 4 cm. If ABE is a quadrant of a circle, find the area of
the shaded region. [Take π = 22/7 ]
Solution.

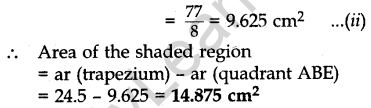
SECTION D
Questions number 21 to 31 carry 4 marks each.
Question.21 Solve for x:
![]()
Solution.

Question.22 In a school, students decided to plant trees in and around the school to reduce air pollution. It was decided that the number of trees, that each section of each class will plant,
will be double of the class in which they are studying. If there are 1 to 12 classes in the school and each class has two Sections, find how many trees were planted by the students. Which value is shown in this question?
Solution.

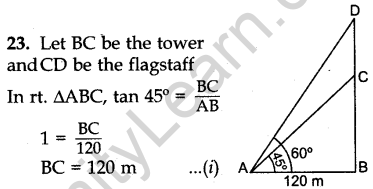
Question.23 The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [Use √3 = 1.73]
Solution.

Question.24 Red queens and black jacks are removed from a pack of 52 playing cards. A card is drawn at random from the remaining cards, after reshuffling them. Find the probability that the drawn card is
(i) a king (ii) of red colour (iii) a face card (iv) a queen
Solution.

Question.25 If A(-3, 5), B(-2, -7), C(l, -8) and D(6, 3) are the vertices of a quadrilateral ABCD, find its area.
Solution.

Question.26 A motorboat whose speed in still water is 18 km/h, takes 1 hour more to go 24 km upstream than to return downstream to the same spot. Find the speed of the stream.
Solution.


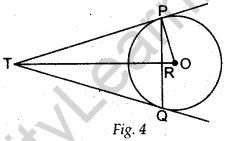
Question.27 In Figure 4, PQ is a chord of length 16 cm, of a circle of radius 10 cm. The tangents at P and Q intersect at a point T. Find the length of TP.
Solution.

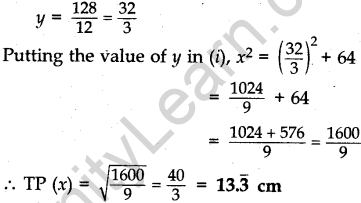
Question.28 Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact
Solution.
![]()
Question.29 150 spherical marbles, each of diameter 1.4 cm, are dropped in a cylindrical vessel of diameter 7 cm containing some water, which are completely immersed in water. Find the rise in the level of water in the vessel.
Solution.

Question.30 A container open at the top, is in the form of a frustum of a cone of height 24 cm with radii of its lower and upper circular ends as 8 cm and 20 cm respectively. Find the cost of milk which can completely fill the container at the rate of Rs 21 per litre. [Use π = 22/7]
Solution.

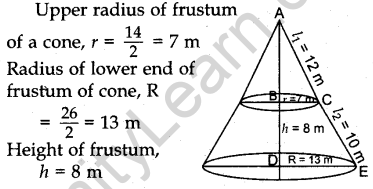
Question.31 A tent consists of a frustum of a cone, surmounted by a cone. If the diameter of the upper and lower circular ends of the frustum be 14 m and 26 m respectively, the height of the frustum be 8 m and the slant height of the surmounted conical portion be 12 m, find the area of canvas required to make the tent. (Assume that the radii of the upper circular end of the frustum and the base of surmounted conical portion are equal).
Solution.

SET II
Note: Except for the following questions, all the remaining questions have been asked in Set-I.
Question.10 Find the values of k for which the quadratic equation 9x2 – 3kx + k = 0 has equal roots.
Solution.

Question.18 The sum of the 2nd and the 7th terms of an AP is 30. If its 15th term is 1 less than twice its 8th term, find the AP.
Solution.
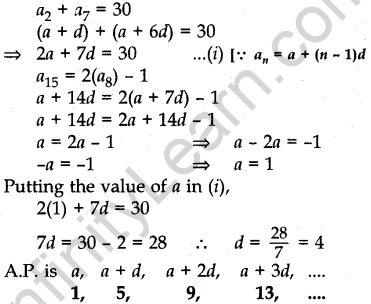
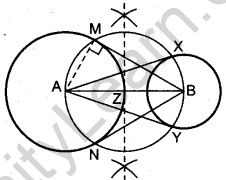
Question.19 Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Solution.

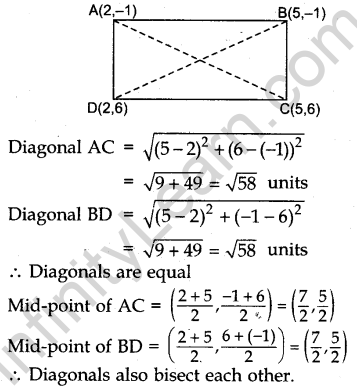
Question.20 Prove that the diagonals of a rectangle ABCD, with vertices A(2, -1), B(5, -1), C(5, 6) and D(2, 6), are equal and bisect each other.
Solution.
Question.27
![]()
Solution.

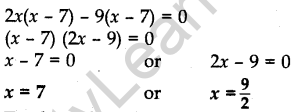
Question.28 All the red face cards are removed from a pack of 52 playing cards. A card is drawn at random from the remaining cards, after reshuffling them. Find the probability that the drawn card is
(i) of red colour (ii) a queen (iii) an ace (iv) a face card
Solution.

Question.29 A(4, -6), B(3, -2) and C(5, 2) are the vertices of a ΔABC and AD is its median. Prove that the median AD divides ΔABC into two triangles of equal areas.
Solution.
![]()
Question.30 Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution.
![]()
SET III
Note: Except for the following questions, all the remaining questions have been asked in Set-I and Set-11.
Question.10 Find the value of p so that the quadratic equation px (x – 3) + 9 = 0 has equal roots.
Solution.
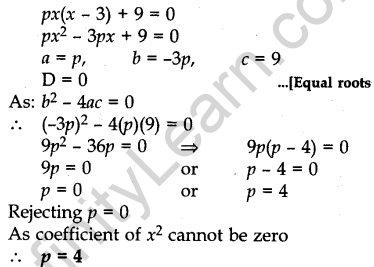
Question.18 The sum of the first seven terms of an AP is 182. If its 4th and the 17th terms are in the ratio 1 : 5, find the AP.
Solution.

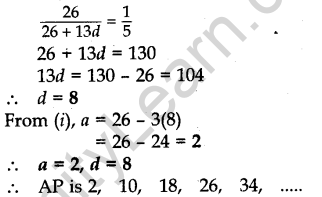
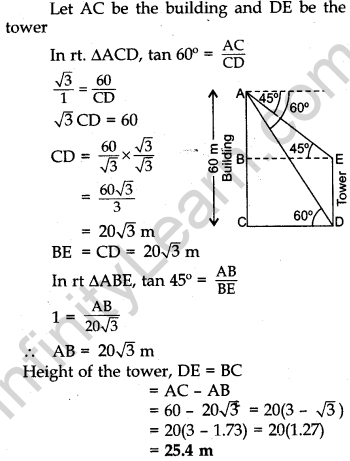
Question.19 From the top of a 60 m high building, the angles of depression of the top and the bottom of a tower are 45° and 60° respectively. Find the height of the tower. [Take √3 = 1.73]
Solution.
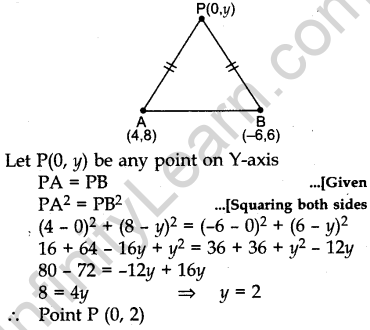
Question.20 Find a point P on the y-axis which is equidistant from the points A(4, 8) and B(-6, 6). Also find the distance AP.
Solution.
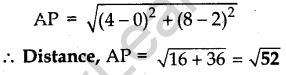
Question.27
![]()
Solution.

Question.28 Five cards—the ten, jack, queen, king and ace of diamonds, are well shuffled with their faces downwards. One card is then picked up at random.
(a) What is the probability that the drawn card is the queen?
(b) If the queen is drawn and put aside, and a second card is drawn, find the probability
that the second card is (i) an ace (ii) a queen.
Solution.

Question.29 If A(4, 2), B(7, 6) and C(l, 4) are the vertices of a ΔABC and AD is its median, prove that the median AD divides ΔABC into two triangles of equal areas.
Solution.


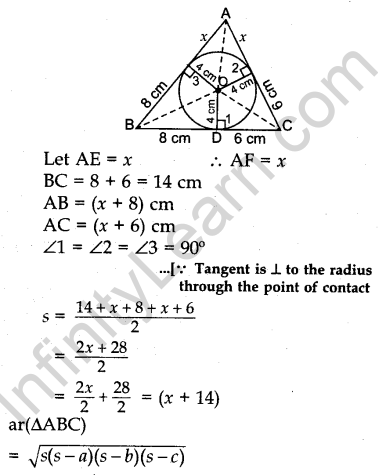
Question.30 In Figure 4, a triangle ABC is drawn to circumscribe a circle of radius 4 cm, such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
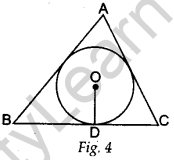
Solution.