Table of Contents
Time Allowed: 3 hours
Maximum Marks: 80
General Instructions:
- All questions are compulsory.
- This question paper consists of 30 questions divided into four sections- A, B, C and D.
- Section A contains 6 questions of 1 mark each, Section B contains 6 questions of 2 marks each, Section C contains 10 questions of 3 marks each and Section D contains 8 questions of 4 marks each.
- There is no overall choice. However, an internal choice has been provided in two questions of 1 mark each, two questions of 2 marks each, four questions of 3 marks each and three questions of 4 marks each. You have to attempt only one of the alternative in all such questions.
- Use of calculators is not permitted.
CBSE Previous Year Question Papers Class 10 Maths 2017 Outside Delhi Term 2 Set I
Section – A
Question 1.
What is the common difference of an A.P. in which a21 – a7 = 84 ? [1]
Solution:
Given, a21 – a7 = 84
⇒ (a + 20d) – (a + 6d) = 84
⇒ a + 20d – a – 6d = 84
⇒ 20d – 6d = 84
⇒ 14d = 84
Hence common difference = 6
Question 2.
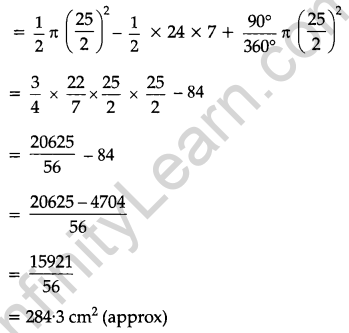
If the angle between two tangents drawn from an external point P to a circle of radius a and centre O, is 60°, then find the length of OP. [1]
Solution:
Given, ∠APB = 60°
∠APO = 30°
In right angle ΔOAP,
\(\frac { OP }{ OA }\) = cosec 30°
⇒ \(\frac { OP }{ a }\) = 2
⇒ OP = 2a
Question 3.
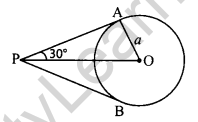
If a tower 30 m high, casts a shadow 10√3 m long on the ground, then what is the angle of elevation of the sun? [1]
Solution:
In ΔABC,
tan θ = \(\frac { AB }{ BC }\)
⇒ tan θ = \(\frac { 30 }{ 10\surd 3 }\) = √3
⇒ tan θ = tan 60°
⇒ θ = 60°
Hence angle of elevation is 60°.
Question 4.
The probability of selecting a rotten apple randomly from a heap of 900 apples is 0-18. What is the number of rotten apples in the heap? [1]
Solution:
Total apples = 900
P(E) = 0.18

No. of rotten apples = 900 × 0.18 = 162
Section – B
Question 5.
Find the value of p, for which one root of the quadratic equation px2 – 14x + 8 = 0 is 6 times the other. [2]
Solution:
Given equation is px2 – 14x + 8 = 0
Let one root = α
then other root = 6α


Question 6.
Which term of the progression 20, 19\(\frac { 1 }{ 4 }\), 18\(\frac { 1 }{ 2 }\), 17\(\frac { 3 }{ 4 }\), … is the first negative term ? [2]
Solution:
Given, A.P. is 20, 19\(\frac { 1 }{ 4 }\), 18\(\frac { 1 }{ 2 }\), 17\(\frac { 3 }{ 4 }\), …..

Question 7.
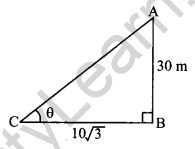
Prove that the tangents drawn at the endpoints of a chord of a circle make equal angles with the chord. [2]
Solution:
Given, a circle of radius OA and centred at O with chord AB and tangents PQ & RS are drawn from point A and B respectively.
Draw OM ⊥ AB, and join OA and OB.
In ∆OAM and ∆OMB,
OA = OB (Radii)
OM = OM (Common)
∠OMA = ∠OMB (Each 90°)
∆OAM = ∆OMB (By R.H.S. Congurency)
∠OAM = ∠OBM (C.PC.T.)
Also, ∠OAP = ∠OBR = 90° (Line joining point of contact of tangent to centre is perpendicular on it)
On addition,
∠OAM + ∠OAP = ∠OBM + ∠OBR
⇒ ∠PAB = ∠RBA
⇒ ∠PAQ – ∠PAB = ∠RBS – ∠RBA
⇒ ∠QAB = ∠SBA
Hence Proved
Question 8.
A circle touches all the four sides of a quadrilateral ABCD. Prove that AB + CD = BC + DA [2]
Solution:
Given, a quad. ABCD and a circle touch its all four sides at P, Q, R, and S respectively.

To prove: AB + CD = BC + DA
Now, L.H.S. = AB + CD
= AP + PB + CR + RD
= AS + BQ + CQ + DS (Tangents from same external point are always equal)
= (AS + SD) + (BQ + QC)
= AD + BC
= R.H.S.
Hence Proved.
Question 9.
A line intersects the y-axis and x-axis at the points P and Q respectively. If (2, -5) is the mid-point of PQ, then find the coordinates of P and Q. [2]
Solution:
Let co-ordinate of P (0, y)
Co-ordinate of Q (x, 0)

Question 10.
If the distances of P(x, y), from A(5, 1) and B(-1, 5) are equal, then prove that 3x = 2y. [2]
Solution:
Given, PA = PB
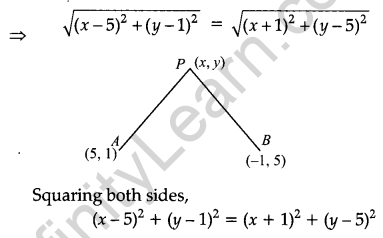
⇒ x2 + 25 – 10x + y2 + 1 – 2y = x2 + 1 + 2x + y2 + 25 – 10y
⇒ -10x – 2y = 2x – 10y
⇒ -10x – 2x = -10y + 2y
⇒ 12x = 8y
⇒ 3x = 2y
Hence Proved.
Section – C
Question 11.
If ad ≠ bc, then prove that the equation (a2 + b2) x2 + 2 (ac + bd) x + (c2 + d2) = 0 has no real roots. [3]
Solution:
Given, ad ≠ bc
(a2 + b2) x2 + 2(ac + bd)x + (c2 + d2) = 0
D = b2 – 4ac
= [2(ac + bd)]2 – 4 (a2 + b2) (c2 + d2)]
= 4[a2c2 + b2d2 + 2abcd] – 4(a2c2 + a2d2 + b2c2 + b2d2)
= 4[a2c2 + b2d2 + 2abcd – a2c2 – a2d2 – b2c2 – b2d2]
= 4[-a2d2 – b2c2 + 2abcd]
= -4[a2d2 + b2c2 – 2abcd]
= -4[ad – bc]2
D is negative
Hence given equation has no real roots.
Hence Proved.
Question 12.
The first term of an A.E is 5, the last term is 45 and the sum of all its terms is 400. Find the number of terms and the common difference of the A.P. [3]
Solution:
Given, a = 5, an = 45, Sn = 400
We have, Sn = \(\frac { n }{ 2 }\) [a + an]
⇒ 400 = \(\frac { n }{ 2 }\) [5 + 45]
⇒ 400 = \(\frac { n }{ 2 }\) [50]
⇒ 25n = 400
⇒ n = 16
Now, an = a + (n – 1) d
⇒ 45 = 5 + (16 – 1)d
⇒ 45 – 5 = 15d
⇒ 15d = 40
⇒ d = \(\frac { 8 }{ 3 }\)
So n = 16 and d = \(\frac { 8 }{ 3 }\)
Question 13.
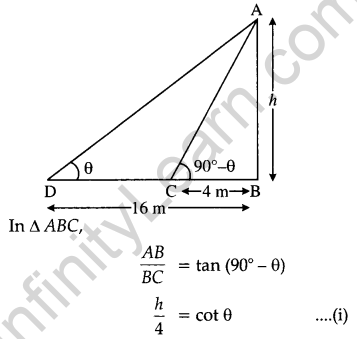
On a straight line passing through the foot of a tower, two points C and D are at distances of 4 m and 16 m from the foot respectively. If the angles of elevation from C and D of the top of the tower are complementary, then find the height of the tower. [3]
Solution:
Let height AB of tower = h m.

Question 14.
A bag contains 15 white and some black balls. If the probability of drawing a black ball from the bag is thrice that of drawing a white ball, find the number of black balls in the bag. [3]
Solution:
Given, no. of white balls = 15
Let no. of black balls = x
Total balls = (15 + x)
According to the question,
P(Blackball) = 3 × P(White ball)
⇒ \(\frac { x }{ 15+x }\) = 3 × \(\frac { 15 }{ 15+x }\)
⇒ x = 45
No. of black balls in bag = 45
Question 15.
In what ratio does the point (\(\frac { 24 }{ 11 }\), y) the line segment joining the points P(2, -2) and Q(3, 7) ? Also, find the value of y. [3]
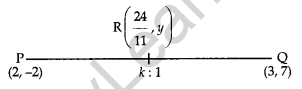
Solution:
Let point R divides PQ in the ratio k : 1
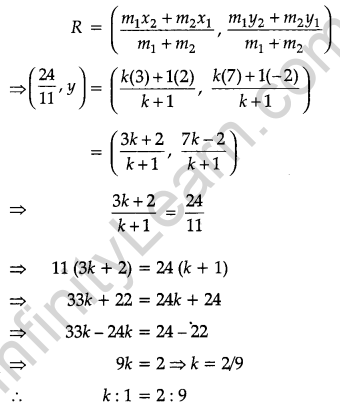

Question 16.
Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semi-circle of radius 4.5 cm are drawn in the given figure. Find the area of the shaded region. [3]
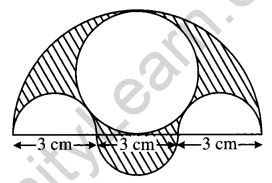
Solution:
Given, radius of large semi-circle = 4.5 cm



Question 17.
In the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. [Use π = \(\frac { 22 }{ 7 }\)]
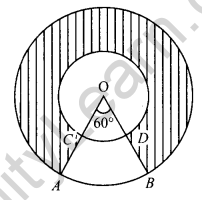
Solution:
Angle for shaded region = 360° – 60° = 300°
Area of shaded region

Question 18.
Water in a canal, 5-4 m wide and 1.8 m deep, is flowing with a speed of 25 km/hour. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation ? [3]
Solution:
Width of canal = 5.4 m
Depth of canal = 1.8 m
Length of water in canal for 1 hr = 25 km = 25000 m
Volume of water flown out from canal in 1 hr = l × b × h = 5.4 × 1.8 × 25000 = 243000 m3
Volume of water for 40 min = 243000 × \(\frac { 40 }{ 60 }\) = 162000 m3
Area to be irrigated with 10 cm standing water in field = \(\frac { Volume }{ Height }\)
= \(\frac { 162000\times 100 }{ 10 }\) m2
= 1620000 m2
= 162 hectare
Question 19.
The slant height of a frustum of a cone is 4 cm and the perimeters of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum. [3]
Solution:
Slant height of frustum ‘l’ = 4 cm
Perimeter of upper top = 18 cm

Question 20.
The dimensions of a solid iron cuboid are 4.4 m × 2.6 m × 1.0 m. It is melted and recast into hollow cylindrical pipe of 30 cm inner radius and thickness 5 cm. Find the length of the pipe. [3]
Solution:
Inner radius of pipe ‘r’ = 30 cm
The thickness of pipe = 5 cm
Outer radius ‘R’ = 30 + 5 = 35 cm
Now, Volume of hollow pipe = Volume of Cuboid

Section – D
Question 21.
Solve for x:
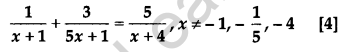
Solution:

Question 22.
Two taps running together can fill a tank in 3\(\frac { 1 }{ 13 }\) hours. If one tap takes 3 hours more than the other to fill the tank, then how much time will each tap take to fill the tank ? [4]
Solution:
Let tank fill by one tap = x hrs
other tap = (x + 3) hrs
Together they fill by 3\(\frac { 1 }{ 13 }\) = \(\frac { 40 }{ 13 }\) hrs

Either x – 5 = 0 or 13x + 24 = 0
x = 5, x = -24/13 (Rejected)
One tap fill the tank in 5 hrs
So other tap fill the tank in 5 + 3 = 8 hrs
Question 23.
If the ratio of the sum of the first n terms of two A.P.S is (7n + 1) : (4n + 27), then find the ratio of their 9th terms. [4]
Solution:
Ratio of the sum of first n terms of two A.P.s are

Hence ratio of 9th terms of two A.P.s is 24 : 19
Question 24.
Prove that the lengths of two tangents drawn from an external point to a circle are equal. [4]
Solution:
Given, a circle with centre O and external point P. |
Two tangents PA and PB are drawn.
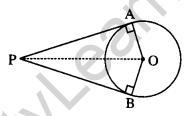
To Prove: PA = PB
Construction: Join radius OA and OB also join O to P.
Proof: In ∆OAP and ∆OBP,
OA = OB (Radii)
∠A = ∠B (Each 90°)
OP = OP (Common)
∆AOP = ∆BOP (RHS cong.)
PA = PB [By C.PC.T.]
Hence Proved.
Question 25.
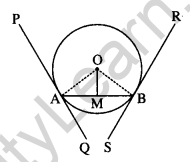
In the given figure, XY and XY are two parallel tangents to a circle with centre O and another tangent AB with a point of contact C, is intersecting XY at A and X’Y’ at B. Prove that ∠AOB = 90°. [4]
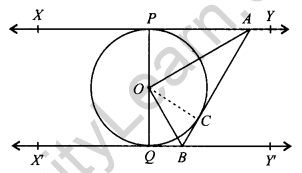
Solution:
Given, XX’ & YY’ are parallel.
Tangent AB is another tangent which touches the circle at C.
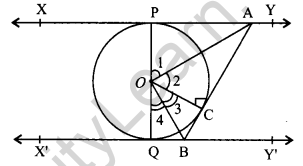
To prove: ∠AOB = 90°
Construction: Join OC.
Proof: In ∆OPA and ∆OCA,
OP = OC (Radii)
∠OPA = ∠OCA (Radius ⊥ Tangent)
OA = OA (Common)
∆OPA = ∆OCA (CPCT)
∠1 = ∠2 …(i)
Similarly, ∆OQB = ∆OCB
∠3 = ∠4 …(ii)
Also, POQ is a diameter of circle
∠POQ = 180° (Straight angle)
∠1 + ∠2 + ∠3 + ∠4 = 180°
From eq. (i) and (ii),
∠2 + ∠2 + ∠3 + ∠3 = 180°
⇒ 2(∠2 + ∠3) = 180°
⇒ ∠2 + ∠3 = 90°
Hence, ∠AOB = 90°
Hence Proved.
Question 26.
Construct a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then construct another triangle whose sides are \(\frac { 3 }{ 4 }\) times the corresponding sides of the ∆ABC. [4]
Solution:
BC = 7 cm, ∠B = 45°, ∠A = 105°
∠C = 180 ° – (∠B + ∠A) = 180° – (45° + 105°) = 180° – 150° = 30°
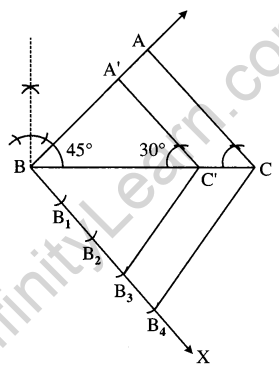
Steps of construction:
- Draw a line segment BC = 7 cm.
- Draw an angle 45° at B and 30° at C. They intersect at A.
- Draw an acute angle at B.
- Divide angle ray in 4 equal parts as B1, B2, B3 and B4.
- Join B4 to C.
- From By draw a line parallel to B4C intersecting BC at C’.
- Draw another line parallel to CA from C’ intersecting AB ray at A.
Hence, ∆A’BC’ is required triangle such that ∆A’BC’ ~ ∆ABC with A’B = \(\frac { 3 }{ 4 }\) AB.
Question 27.
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. [Use √3 = 1.732] [4]
Solution:
Let aeroplane is at A, 300 m high from a river. C and D are opposite banks of river.

Question 28.
If the points A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear, then find the value of k. [4]
Solution:
Since A(k + 1, 2k), B(3k, 2k + 3) and C(5k – 1, 5k) are collinear points, so area of triangle = 0.

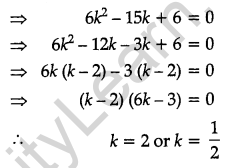
Question 29.
Two different dice are thrown together. Find the probability that the numbers obtained have
(i) even sum, and
(ii) even product. [4]
Solution:
When two different dice are thrown together
Total outcomes = 6 × 6 = 36
(i) For even sum: Favourable outcomes are
(1, 1), (1, 3), (1, 5), (2, 2), (2, 4), (2, 6),
(3, 1), (3, 3), (3, 5), (4, 2), (4, 4), (4, 6),
(5, 1), (5, 3), (5, 5), (6, 2), (6, 4), (6, 6)
No. of favourable outcomes = 18
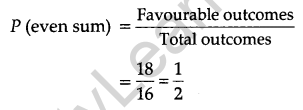
(ii) For even product: Favourable outcomes are
(1, 2), (1, 4), (1, 6), (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
(3, 2), (3, 4), (3, 6), (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
(5, 2), (5, 4), (5, 6), (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6).
No. of favourable outcomes = 27
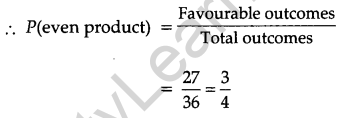
Question 30.
In the given figure, ABCD is a rectangle of dimensions 21 cm × 14 cm. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the figure. [4]

Solution:
Area of Shaded region = Area of a rectangle – Area of a semi-circle

Question 31.
In a rain-water harvesting system, the rainwater from a roof of 22 m × 20 m drains into a cylindrical tank having a diameter of base 2 m and height 35 m. If the tank is full, find the rainfall in cm. Write your views on water conservation. [4]
Solution:
Volume of water collected in system = Volume of a cylindrical tank

CBSE Previous Year Question Papers Class 10 Maths 2017 Outside Delhi Term 2 Set II
Note: Except for the following questions, all the remaining questions have been asked in previous sets.
Section – B
Question 10.
Which term of the A.P. 8, 14, 20, 26,… will be 72 more than its 41st term? [2]
Solution:
A.P. is 8, 14, 20, 26,….
a = 8, d = 14 – 8 = 6
Let an = a41 + 72
a + (n – 1)d = a + 40d + 72
⇒ (n – 1) 6 = 40 × 6 + 72 = 240 + 72 = 312
⇒ n – 1 = 52
⇒ n = 52 + 1 = 53rd term
Section – C
Question 18.
From a solid right circular cylinder of height 24 cm and radius 0.7 cm, a right circular cone of the same height and same radius is cut out. Find the total surface area of the remaining solid. [3]
Solution:
Given,
Height of cylinder ‘h’ = 2.4 cm,
Radius of base ‘r’ = 0.7 cm


Question 19.
If the 10th term of an A.E is 52 and the 17th term is 20 more than the 13th term, find the A.P. [3]
Solution:
Given, a10 = 52;
a17 = a13 + 20
⇒ a + 16d = a + 12d + 20
⇒ 16d = 12d + 20
⇒ 4d = 20
⇒ d = 5
Also, a + 9d = 52
⇒ a + 9 × 5 = 52
⇒ a + 45 = 52
⇒ a = 7
Therefore A.E = 7, 12, 17, 22, 27,….
Question 20.
If the roots of the equation (c2 – ab) x2 – 2(a2 – bc) x + b2 – ac = 0 in x are equal, then show that either a = 0 or a3 + b3 + c3 = 3abc. [3]
Solution:

Section – D
Question 28.
Solve for x:
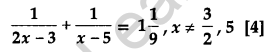
Solution:
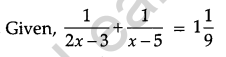

Question 29.
A train covers a distance of 300 km at a uniform speed. If the speed of the train is increased by 5 km/hour, it takes 2 hours less on the journey. Find the original speed of the train. [4]
Solution:
Let original speed of train = x km/hr
Increased speed of train = (x + 5) km/hr
Distance = 300 km
According to the question,

Question 30.
A man observes a car from the top of a tower, which is moving towards the tower with a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower. [4]
Solution:
Let AB is a tower, the car is at point D at 30° and goes to C at 45° in 12 minutes.
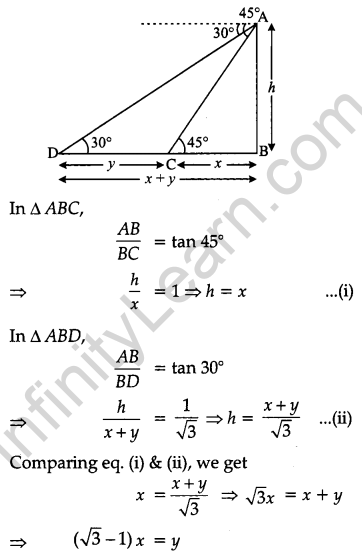

Question 31.
In the given figure, ΔABC is a right-angled triangle in which ∠A is 90°. Semi-circles are drawn on AB, AC and BC as diameters. Find the area of the shaded region. [4]
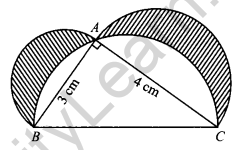
Solution:
In right ΔBAC, by Pythagoras theorem,
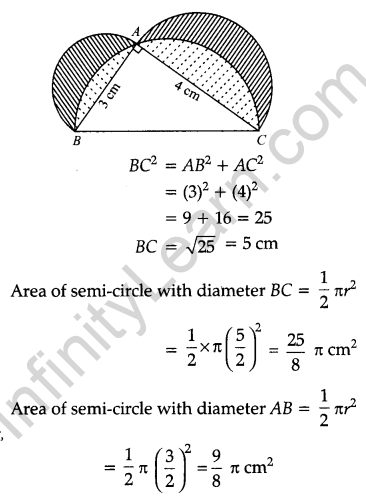

CBSE Previous Year Question Papers Class 10 Maths 2017 Outside Delhi Term 2 Set III
Note: Except for the following questions, all the remaining questions have been asked in previous sets.
Section – B
Question 10.
For what value of n, are the terms of two A.Ps 63, 65, 67,…. and 3, 10, 17,…. equal ? [2]
Solution:
1st A.P. is 63, 65, 67,…
a = 63, d = 65 – 63 = 2
an = a + (n – 1 )d = 63 + (n – 1) 2 = 63 + 2n – 2 = 61 + 2n
2nd A.E is 3, 10, 17,…
a = 3, d = 10 – 3 = 7
an = a + (n – 1 )d = 3 + (n – 1) 7 = 3 + 7n – 7 = 7n – 4
According to question,
61 + 2n = 7n – 4
⇒ 61 + 4 = 7n – 2n
⇒ 65 = 5n
⇒ n = 13
Hence, 13th term of both A.P. is equal.
Section – C
Question 18.
A toy is in the form of a cone of radius 3-5 cm mounted on a hemisphere of the same radius on its circular face. The total height of the toy is 15*5 cm. Find the total surface area of the toy. [3]
Solution:
Given, radius of base ‘r’ = 3.5 cm
Total height of toy = 15.5 cm
Height of cone ‘h’ = 15.5 – 3.5 = 12 cm
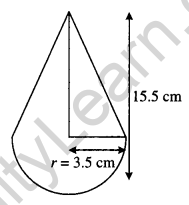

Question 19.
How many terms of an A.E 9, 17, 25,… must be taken to give a sum of 636? [3]
Solution: A.P. is 9, 17, 25,….,
Sn = 636
a = 9, d = 17 – 9 = 8

Question 20.
If the roots of the equation (a2 + b2) x2 – 2 (ac + bd) x + (c2 + d2) = 0 are equal, prove that \(\frac { a }{ b }\) = \(\frac { c }{ d }\) [3]
Solution:

Section – D
Question 28.
Solve for x:

Solution:

Question 29.
A takes 6 days less than B to do a work. If both A and B working together can do it in 4 days, how many days will B take to finish it? [4]
Solution:
Let B can finish a work in x days
so, A can finish work in (x – 6) days
Together they finish work in 4 days
Now,
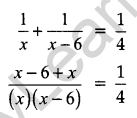
⇒ 4 (2x – 6) = x2 – 6x
⇒ 8x – 24 = x2 – 6x
⇒ x2 – 14x + 24 = 0
⇒ x2 – 12x – 2x + 24 = 0
⇒ x(x – 12) – 2(x – 12) = 0
⇒ (x – 12) (x – 2) = 0
Either x – 12 = 0 or x – 2 = 0
x = 12 or x = 2 (Rejected)
B can finish work in 12 days
A can finish work in 6 days.
Question 30.
From the top of a tower, 100 m high, a man observes two cars on the opposite sides of the tower and in a same straight line with its base, with angles of depression 30° and 45°. Find the distance between cars.
[Take √3 = 1.732] [4]
Solution:
Let AB is a tower.
Cars are at point C and D respectively
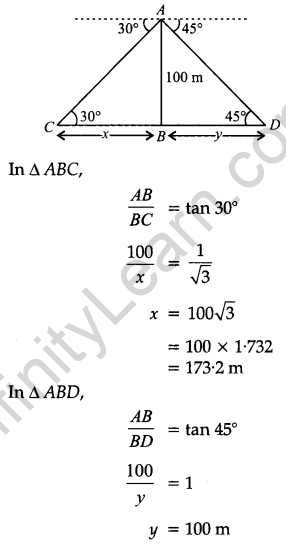
Distance between two cars = x + y = 173.2 + 100 = 273.2 m
Question 31.
In the given figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region. [4]
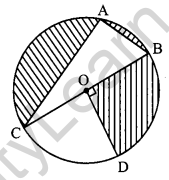
Solution:
Given, C (O, OB) with AC = 24 cm AB = 7 cm and ∠BOD = 90°
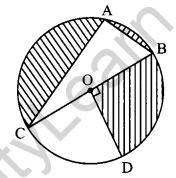
∠CAB = 90° (Angle in semi-circle)
Using pythagoras theorem in ∆CAB,
BC2 = AC2 + AB2 = (24)2 + (7)2 = 576 + 49 = 625
⇒ BC = 25 cm
Radius of circle = OB = OD = OC = \(\frac { 25 }{ 2 }\) cm
Area of shaded region = Area of semi-circle with diamieter BC – Area of ∆CAB + Area of sector BOD