Table of Contents
Two laws of electricity, given by German physicist, G. R. Kirchhoff, form the foundation for simplifying complex electrical circuits and analysis of electrical circuits. As an analogy, they are as important to electrical circuits as Newton’s laws are for solving problems on mechanics. That puts their importance in perspective.

At the heart of these two laws, lie more fundamental laws about charges and energy. So understanding Kirchhoff’s laws is indirectly applying basic laws about charges and energy for electrical circuits.
Kirchhoff’s laws can be applied to any electrical circuit, involving capacitors, resistors, inductors, batteries, transistors, diodes, triodes etc.
Some important definitions before we state and elaborate Kirchhoff’s laws
Circuit
A circuit is a closed loop in which electrons and/or ions can travel in. Required force or energy to make the electrons/ions move is usually provided by battery.
Node
Conducting wires are generally regarded to be without resistance. A node is a region where the terminals of two or more circuit elements connect, including any wires or conductors between them.
Junction: It is a point in a circuit at which current splits.
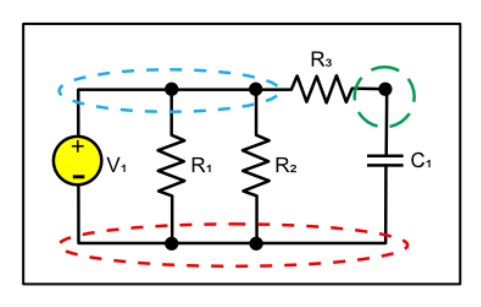
In the above diagram, circuit elements are represented in black, nodes are shown in colour and junctions are represented by dots in black. Note that junction is a point whereas node is a region.
Branch
Circuit region between two neighbouring junctions can normally be referred as a branch.
Loop
A closed path covering circuit elements.
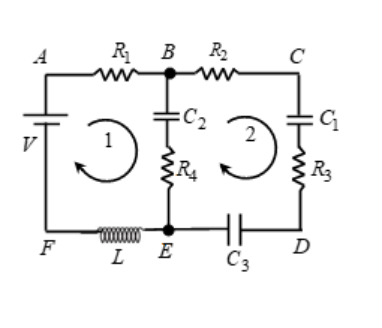
In the above circuit:
| Junctions | B and E are junctions because here current splits |
| Loops | ABEFA, BCDEB and ABCDEFA are loops |
| Branch | BE is a branch. |
Now let us venture into stating and elaborating Kirchhoff’s laws.
Kirchhoff’s first law
It is also known as junction law or current law.
It states that total current entering a junction is always equal to total current leaving a junction. We know current is nothing but charges in motion. What the first law implies is that as many charges enter a junction in a given time, that many charges also leave the junction in the same amount of time. It is true because a junction is NOT a point which eats up charges, nor is it a point where charges accumulate or are generated A junction is just a guide to split incoming charges into multiple outgoing paths.
Hence, Kirchhoff’s first law is a consequence of law of conservation of charge.
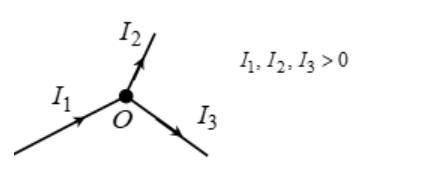
As per first law, if current enters I1 the junction O whereas I2 and I3 leave the junction, then
I1 = I2 + I3
NOTE: If a convention is adopted, say incoming currents will be called positive and outgoing currents will be called negative, then the junction law says that algebraic sum of currents meeting at a junction is always zero.
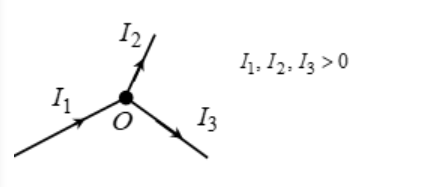
I1 + ( – I2) + ( I3 )= 0
=> I1 = I2 + I3
Problem 1
Find the value of I3.
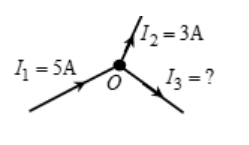
Solution
I1 = I2 + I3 => I2 + I3 = 5 => 3 + I3
=> I3 = 2A
So, by making use of the first law, you can find out unknown currents.
Let us check one more example.
Problem 2
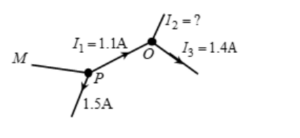
- Find the magnitude and direction of current in PM
- Find the magnitude and direction of current I2
Solution
- At P : There are three branches meeting at the junction, out of which for 2 of them, we are given known currents. Two (given) currents are outgoing from the junction. Therefore the third current must be incoming. Total outgoing current at the junction is 1.1 + 1.5 = 2.6A. So total incoming current should also be 2.6A.
=> IMP = 1.1 + 1.5 = 2.6A (incoming). - Let I2 be outgoing current. Then by junction law,
- I1 = I2 + I3
- 1.1 = I2 + 1.4
- I2 = -0.3A.
Negative sign indicates that direction of I2is actually opposite to our assumption. So, the currents are:
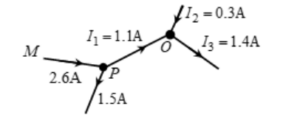
Kirchhoff’s second law
It is also known as Kirchhoff’s voltage law or Kirchhoff’s loop law.
Statement: The algebraic sum of voltages across various circuit elements around a closed loop is zero.
Mathematically, 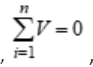 ,
,
where n stands for number of circuit elements in a loop.
You know voltage (potential difference) refers to work done per unit charge between two points. What the law says is if you traverse a loop along one sense, say clockwise, (and importantly you come back to same point) and keep noting down voltage drops across various circuit elements in the loop, then you will get sum total of these voltages equal to zero. Naturally, if some voltages are positive, then some others must be negative so that sum total is zero.
Kirchhoff’s second law is a consequence of law of conservation of energy. In a closed loop, there are sources that produce electrical energy and there are sinks where this energy is used.
There is a convention adopted to assign signs to voltages.
How to apply the convention of sign for voltages?
Assign currents along various branches of the given circuit following Kirchhoff’s first law. Assign charges on the capacitor(s), if any, using conservation of charge.
Consider a closed loop of the given circuit. Decide on the direction in which you wish to traverse the loop (clockwise or anticlockwise).
Below are given conventions for assigning signs for voltages across resistors, batteries and capacitors.
Resistor
While traversing the loop, at a resistor, if we move along the direction of current, then voltage drop across it is considered negative.
While traversing the loop, at a resistor, if we move opposite to the direction of current, then voltage drop across it is considered positive.
Capacitor
While traversing the loop, at a capacitor, if we move from the positive plate to the negative plate, then voltage drop across it is considered negative.
While traversing the loop, at a capacitor, if we move from the negative plate to the positive plate, then voltage drop across it is considered positive.
Battery
While traversing the loop, at a battery, if we move from the positive terminal to the negative terminal inside the battery, then voltage drop across it is considered negative.
While traversing the loop, at a battery, if we move from the negative terminal to the positive terminal inside the battery, then voltage drop across it is considered positive.
Problem 3
Find the magnitude and direction of current through the given circuit.
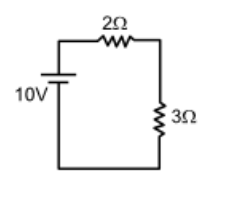
Solution:
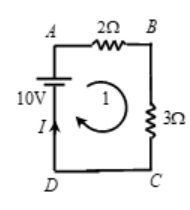
Let the magnitude of current be and its direction be as indicated.
Traversing the loop along the direction of the loop shown, and applying Kirchhoff’s second law, we get,
+10 – 2(I) – 3(I) = 0
=> I = 10/5 = 2A
Current is flowing clockwise.
Problem 4
In the previous problem, assign direction of current opposite to as assigned earlier and solve the problem. What is your inference?
Solution:
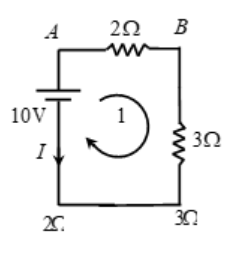
Only direction of current is shown reversed.
Traversing the loop along the direction of the loop shown, and applying Kirchhoff’s second law, we get,
+10 – 2(I) – 3(I) = 0
=> I = – 10/5 = 2A
Negative sign for current indicates magnitude of current is 2A but its direction is opposite to the one we assumed. So current is actually flowing clockwise.
Inference: Initially we can assign direction of current by making assumption. Kirchhoff’s laws help to find the actual direction of current regardless of what we assume.
Problem 5
Find currents in the given circuit.
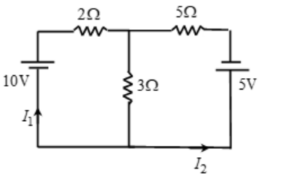
Solution:
By applying Kirchhoff’s first law, currents and their directions are assigned as shown. Note, at junction B, current I1 + I2 flows from B to E
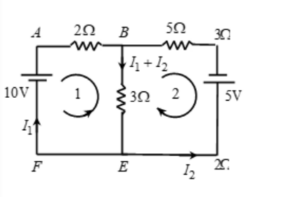
Applying KVL to loop 1 (traversing anticlockwise)
-10 + 3(I1 + I2) + 2I1 = 0
=> 5I1 + 3I2 = 10 …(1)
Applying KVL to loop 2 (traversing clockwise)
3(I1 + I2) + 5I2 + 5 = 0
=>3I1 + 8I2 = 5 …(2)
From (1) and (2), we get,
I1 = 95/31A, I2 = -55/31A
Negative sign of I2 indicates its direction is actually opposite to the one indicated.
Frequently Asked Questions on Kirchhoff’s laws
What is Kirchhoff’s first law?
Kirchhoff’s first law, also known as current law, states that algebraic sum of currents meeting at a junction is zero.
What is Kirchhoff’s second law?
Algebraic sum of voltage drops across various circuit elements of a closed loop is zero.
What are the uses of Kirchhoff’s laws?
Unknown voltages and currents in a circuit can be found.
When are Kirchhoff’s laws valid?
They are valid when there is no induced electric field inside the circuit. Kirchhoff’s laws work only for conservative electric fields (those NOT generated by changing magnetic field).
Are Kirchhoff’s laws applicable for circuits involving inductors?
Yes, Kirchhoff’s laws applicable for all types of electrical circuit elements.







