Table of Contents
Introduction to Unit vector
A unit vector is a one-dimensional vector with a magnitude of one that is used to indicate direction without affecting the scale of a measurement. It aids in the definition of orientations in subjects like as physics and engineering. A unit vector, denoted as u, keeps the direction of a given vector v while removing its magnitude, making it a useful tool for describing directions in a standardised manner.
Definition of unit vector and notation
A unit vector is a vector that has a magnitude of 1 and points in a specific direction. It is often used to define the direction of other vectors without changing their scale. The notation for a unit vector is typically represented by a caret symbol (^) placed above the vector’s symbol, like v̂ or û, to indicate that it is a unit vector.
Unit vector formula
The formula to find the unit vector v of a given vector v is:
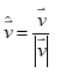
Here, v is the vector for which you want to find the unit vector, and |v| represents the magnitude of vector v. This formula scales the components of v by dividing them by its magnitude, resulting in a vector with a magnitude of 1 and the same direction as v.
How to find the unit vector
To find the unit vector of a given vector v, follow these steps:
- Calculate the magnitude |v| of the vector v.
- Divide each component of v by its magnitude to normalize the vector.
- The resulting normalized vector is the unit vector v̂.
Example:
Given vector v = (3, -4, 5), find its unit vector.
Calculate the magnitude: |v| = √(3² + (-4)² + 5²) = √50.
Normalize the vector: v̂ = (3/√50, -4/√50, 5/√50).
So, the unit vector of v is approximately (0.424, -0.565, 0.707).
Also Check For Relevant Topics:
Solved examples on unit vectors
Example 1: Finding the Unit Vector
Given vector v = (2, -3, 6), find its unit vector v̂.
Solution:
Calculate the magnitude: |v| = √(2² + (-3)² + 6²) = √49 = 7.
Normalize the vector: v̂ = (2/7, -3/7, 6/7).
So, the unit vector of v is (2/7, -3/7, 6/7).
Example 2: Unit Vector in a Specific Direction
Given vector u = (4, 1), find a unit vector in the same direction.
Solution: Calculate the magnitude: |u| = √(4² + 1²) = √17.
Normalize the vector: û = (4/√17, 1/√17).
So, the unit vector in the direction of u is approximately (0.943, 0.333)..
Frequently Asked Questions on Direction Cosines
What is the unit vector and example?
A unit vector is a vector with a magnitude of 1 that points in a specific direction. It's often used to describe direction without affecting scale. The unit vector of a given vector v is represented as v̂ and is calculated by dividing each component of v by its magnitude |v|. Example: Given vector A = (3, -4), find its unit vector Â. Solution: Magnitude of A: |A| = √(3² + (-4)²) = 5. Unit vector  = (3/5, -4/5). So, the unit vector of A is (0.6, -0.8), indicating its direction without changing its magnitude.
What are the 3-unit vectors along coordinate axes?
In a three-dimensional Cartesian coordinate system (x, y, z), there are three unit vectors that point along the coordinate axes: î (i-hat): This unit vector points along the positive x-axis. î = (1, 0, 0) ĵ (j-hat): This unit vector points along the positive y-axis. ĵ = (0, 1, 0) k̂ (k-hat): This unit vector points along the positive z-axis. k̂ = (0, 0, 1) These unit vectors help define the directions of the x, y, and z axes in three-dimensional space and are fundamental for vector representation and calculations.
What is unit vector and zero vector?
A unit vector is a vector that has a magnitude of 1 and points in a specific direction. It is often used to indicate direction without changing the scale of a measurement. The unit vector u of a given vector v is calculated as u = v / |v|, where |v| represents the magnitude of vector v. A zero vector is a vector with no magnitude or direction. It is denoted as 0 or 0̂ and has all its components equal to zero. In vector addition, adding the zero vector to any vector doesn't change its value. The zero vector serves as the additive identity in vector operations.
What is unit vector and its properties?
unit vector is a vector with a magnitude of 1 that points in a specific direction. It is often used to indicate direction without changing the scale of a measurement. The unit vector u of a given vector v is calculated as u = v / |v|, where |v| represents the magnitude of vector v. Properties of unit vectors: Magnitude: The magnitude of a unit vector is always 1: |u| = 1. Direction: Unit vectors have the same direction as the original vector but no change in scale. Normalization: Dividing any vector by its magnitude yields its corresponding unit vector. Addition: Unit vectors can be added like any other vectors, preserving direction and magnitude 1. Unit vectors play a crucial role in defining directions and simplifying vector calculations.
Why is it called a unit vector?
A unit vector is called so because it has a length or magnitude of 1 unit. A unit vector is a vector that has a length of 1 unit, while maintaining the same direction as the original vector. Unit vectors are particularly useful in various mathematical and physical contexts
Which vector has zero magnitude?
A vector with zero magnitude is called the zero vector or the null vector. The zero vector is denoted by 0 or 0̂ (with a hat symbol). It doesn't have a specific direction because it has no length. In other words, all components of the zero vector are equal to zero.
What is unit vector another name?
Another name for a unit vector is a normalized vector. When you normalize a vector, you divide it by its magnitude to create a vector that has a length of 1 unit while maintaining the same direction. This normalized vector is also referred to as a unit vector because it has a magnitude of 1. So, the terms unit vector and normalized vector are often used interchangeably to describe a vector with a length of 1 and the same direction as the original vector.
What is unit vector used for?
Unit vectors, with a magnitude of 1, simplify direction representation, vector decomposition, and normalization. They aid in linear algebra, physics, computer graphics, and more, facilitating calculations involving direction without the complexity of magnitude.
Are all unit vectors equal?
No, not all unit vectors are equal. Unit vectors can have distinct directions even if they have the same magnitude of one. Only when two unit vectors have the same direction in space are they regarded equal.
How do you write unit vector?
Unit vectors are commonly indicated by putting a hat () symbol over the letter denoting the vector quantity. This signifies that the vector has been normalised to have a magnitude of one.









