Table of Contents
In physics, astronomy, and engineering, ellipses are prevalent. For example, each planet’s orbit in the Solar System is roughly an ellipse, with the Sun at one focus point (more accurately, the Sun–planet pair’s barycenter). Moons orbiting planets and all other systems of two astronomical bodies are the same. Ellipsoids are widely used to describe the forms of planets and stars. When viewed from a side angle, a circle seems to be an ellipse: the ellipse is the image of a circle projected in parallel or perspective projection. The ellipse is also the simplest Lissajous figure, generated when horizontal and vertical motions have the same frequency: elliptical polarization of light is caused by a similar process.
Ellipse
- The locus of all those locations in a plane whose sum of distances from two fixed points in the plane is constant is called an ellipse. The foci (singular focus) are the fixed points that are encircled by the curve. The constant ratio is the eccentricity of the ellipse, and the fixed line is the directrix. Eccentricity is a property of the ellipse that indicates its elongation and is symbolized by the letter ‘e.’
- The area of an ellipse is specified by its major and minor axes, and the shape of the ellipse is oval. The area of an ellipse is equal to ab, where a and b are the lengths of the ellipse’s semi-major and semi-minor axes, respectively. Ellipse is analogous to other parts of the conic section that are open in shape and unbounded, such as parabola and hyperbola.
Definition:
In terms of locus, an ellipse is the set of all points on an XY plane whose distance from two fixed points (known as foci) equals a constant value. When a plane slices the cone at an angle with the base, the ellipse is one of the conic sections that results. A circle is formed when the cone is intersected by a plane parallel to the base.
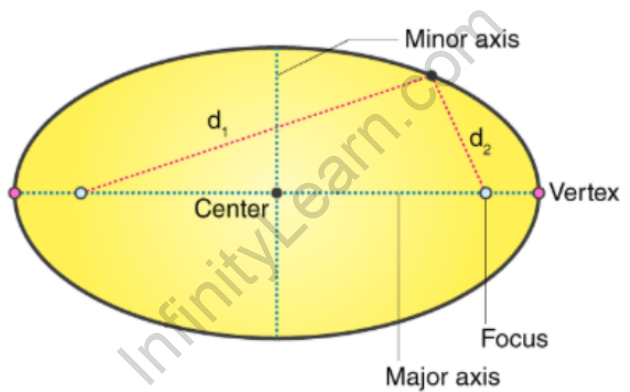
The shape of an ellipse
- An ellipse is a two-dimensional shape specified along its axes in geometry. When a cone is intersected by a plane at an angle to its base, an ellipse is created.
- It has two main sites of interest. For all points in a curve, the total of the two distances to the focal point is always constant.
- A circle is an ellipse in which the foci are all at the same location, which is the circle’s centre.
Ellipse is defined by its two-axis along x and y-axis:
- The major axis is the ellipse’s longest diameter (typically represented by ‘a’), which runs through the centre of the ellipse from one end to the other at the broadest point.
- The minor axis, on the other hand, is the ellipse’s shortest diameter (denoted by ‘b’), passing through the centre at its narrowest point.
- The semi-major axis is half of the major axis, while the semi-minor axis is half of the minor axis.
Properties:
- Ellipse has two focal points, which are also known as foci.
- A directrix is a term for a definite distance.
- The eccentricity of an ellipse ranges from 0 to 1.
- The total sum of any distance between an ellipse’s locus and its two focal points is constant.
- The ellipse has one major and one minor axis, as well as a center.
The eccentricity of the Ellipse
The eccentricity of the ellipse is defined as the ratio of distances from the centre of the ellipse to either focus to the semi-major axis of the ellipse.
e = c/a is the eccentricity of an ellipse.
The focal length is c, while the length of the semi-major axis is a.
FAQs:
What is the definition of the ellipse?
A plane forms an ellipse when it crosses a cone at an angle with respect to the base. It's a curve with two focal points on either side. Ellipse is a collection of points whose distances from two foci are equal.
What is the difference between an ellipse major and a minor?
The ellipse's primary axis runs parallel to the x-axis and has the greatest width. It measures 2a in length. The vertices of the main axis, with coordinates (ha, k), are the endpoints. The minor axis runs parallel to the y-axis and has the shortest width. It measures 2b in length. The vertices of the minor axis with coordinates (h, kb) are the endpoints.