Table of Contents
Motion is the change with time of the position or orientation of an object. The movement or motion along a line or a curve is called translation. Motion that changes the orientation of an object is called rotation. In both cases, every point in the object has the same velocity (directed speed) and the same acceleration (time rate of change of velocity). The most kind of motion combines both translation and rotation.
Each and every movement is relative to some frame of reference. If a body is at rest, it means that it is not in motion but means that it is being described with respect to a frame of reference that is moving together with the body. For example, an object on the surface of the earth may appear to be at rest, but that is only because the observer is also on the surface of the earth. As we know, the motions of objects obey Newton’s laws of motion. The motion at speeds close to the speed of light must be treated by using the theory of relativity, and the motion of very small bodies (such as electrons) must be treated by using quantum mechanics.
Overview
An object moving along the circumference of the circle with a constant speed is said to be exhibiting a circular motion. If an object or body moves in a circular trajectory around one point, then it is said to be performing a circular motion. Consider the example, a car turning on the road is performing a circular motion around some centre. So, the circular motion of continued is periodic in nature. We can say periodic motions are the motions that repeat themselves after a certain period of time. This motion can be classified into two categories based on velocity and acceleration, uniform circular motion and non-uniform circular motion. The name “uniform circular motion” itself says it all. This will examine how objects behave when moving in a circular path at a constant speed. If a body travels in a circular motion along the circumference of a circular trajectory in such a way that its speed keeps changing, then it is called a non-uniform circular motion.
Now, it is seen that uniform circular motion is a specific type of motion in which an object travels in a circle with a constant speed. Consider the example, any point on a propeller spinning at a constant rate is executing uniform circular motion. So, it is remarkable that points on these rotating objects are actually accelerating, although the rotation rate is constant. To see this, we should analyze the motion in terms of vectors. In uniform circular motion, the angular rate of rotation and speed will be constant, while during non-uniform motion, the rate of rotation keeps changing.
Dynamics of Circular Motion
In a circular motion, the object is moving at a constant speed. Consider that the radius of the circular trajectory on which the object is moving is “r”, and the speed of the object is v m/s. The picture shows the object going from point A to point B in time “t”.
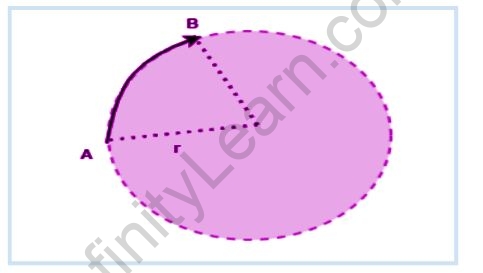
Here, the length of the arc from point A to point B is denoted by “s”. Now, the angle covered by the object is given by,
θ=PQ/r
θ=s/r
The angular velocity of the object can be defined as the rate of change of angle. It is the same as the velocity in the case of straight-line motion, and it is denoted by the Greek symbol ω.
Now,
ω=dθ/dt
By using this,
ω=d/dt (s/r)
ω=(ds/dt) 1/r
Here, S is the length of an arc, which is the distance covered by the object,
V=ds/dt, where ” V” is considered as the speed of the body.
When substituting the value in the equation,
ω=(ds/dt) 1/r
ω=v/r
Uniform Circular motion
We know that objects have a tendency to move in a straight line. There must be some force that keeps them on a circular path for the objects making a circular motion at a constant speed. This force is known as the centripetal force, and the reaction of such a force is called centrifugal force. Thus, we can say that both these forces are equal and opposite in direction.
Now, centrifugal force is given by,
F=(mv^2)/r
It is known that
ω=v/r
When substituting this relation into the equation,
F=(mv^2)/r
F=(m(rω)^2)/r
F=mrω^2
If an object tied to a string is rotated in the horizontal plane by virtue of the tension in the string, then the tension in the string provides the centripetal force for uniform circular motion. We need to understand that this force description is actually an approximation because it does not take into account the downward force due to gravity. In fact, it is not possible to have a horizontal uniform circular motion (except in the region of zero gravity) by keeping the string in a horizontal plane. This is because the gravitational pull will change the plane of the string and the tension in it.
Dynamics of Uniform Circular Motion
Because an object moving in a circle has an acceleration that points toward the centre of the circle, there must be a net force toward the centre to cause this acceleration.
We have already examined Newton’s Laws as they apply to linear motion. That is, we have examined how forces change the magnitude of the velocity of an object but not how forces affect an object’s direction. It is known that velocity is a vector quantity, with both speed and direction; when an object moves with uniform speed in a circular path, its velocity, therefore, undergoes constant change, meaning it experiences acceleration. So, we can consequently analyze uniform circular motion using Newton’s Laws.
Examples of Uniform Circular Motion
The movement or motion of an artificial satellite orbiting around the earth is an example of uniform circular motion. Here, the gravitational force from the earth makes the satellites stay in the circular orbit around the earth.
The movement or motion of electrons about the nucleus.
The movement of blades of the windmills.
The tip of the second hand of a watch with a circular dial represents uniform circular motion.
The small stone is tied to a rope and is being swung in circles.
Also read: Longitudinal and Transverse Wave
Frequently Asked Questions (FAQs)
How do you differentiate between uniform circular motion and non-uniform circular motion?
In a uniform circular motion, the movement of an object along a circular path with constant speed. Whereas, in a non-uniform circular motion, the movement of an object along a circular path with variable speed.
What is an example of uniform circular motion?
The movement or motion of an artificial satellite orbiting around the earth. Here, the gravitational force from the earth makes the satellites stay in the circular orbit around the earth.
What is an example of non-uniform circular motion?
The oscillation of a pendulum represents the non-uniform circular motion.
What changes in the uniform circular motion?
The acceleration stays the same in a uniform circular motion. So, the thing that changes is the Velocity. This happens because the object's direction is always changing. In simple words, velocity is said to be a vector quantity, and it depends upon the direction.





