CBSE Class 6 Maths Notes Chapter 8 Decimals
Dot represents a decimal point.
Thus, five rupees seventy-five paise = ₹ 5.75
Seven rupees fifty paise = ₹ 7.50.
Tenths
To understand the parts of one whole (i.e., a unit) we show a unit by a block. Thus two units are two blocks and so on. One block divided into 10 equal parts means each part is \(\frac { 1 }{ 10 }\) (one- tenth) of a unit, two parts are 2-tenths, five parts are 5-tenths and so on. \(\frac { 1 }{ 10 }\) in decimal notation is written as 0.1. The dot represents the decimal point and it comes between the units place and tenths place.
Every fraction with denominator 10 can be written in decimal notation and vice-versa.
For example:
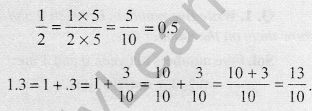
Hundredths
One block divided into 100 equal parts means each part is \(\frac { 1 }{ 100 }\) (one-hundredth) of a unit. It can be written as 0.01 in decimal notation.
Every fraction with denominator 100 can be written in decimal notation and vice-versa.
In place value table, as we go from left to right, then at every step the multiplying factor becomes \(\frac { 1 }{ 10 }\) of the previous factor. The place value table can be further extended from hundredths to \(\frac { 1 }{ 10 }\) of hundredths, i.e., thousandths (\(\frac { 1 }{ 100 }\)), which is written as 0.001 in decimal notation.
All the decimals can be represented on a number line.
Every decimal can be written as a fraction.
We can compare any two decimals. The process of comparison starts with the whole part. If the whole parts are equal then the tenths parts are compared. If the tenths parts are also equal then hundredths parts arc compared and so on.
Decimals are used in numerous ways in our lives. For example in representing units of money, length and weight.
Money
1 paisa = ₹ \(\frac { 1 }{ 100 }\) = ₹ 0.01
85 paise = ₹ \(\frac { 85 }{ 100 }\)— = ₹ 0.85
125 paise = ₹ 1 and 25 paise = ₹ 1.25
Length
1 cm = \(\frac { 1 }{ 100 }\) m = 0.01 m
46 cm = \(\frac { 46 }{ 100 }\) m = 0.46 m
126 cm = 100 cm + 26 cm = 1 m + \(\frac { 26 }{ 100 }\) m = 1.26 m
Weight
1 g = \(\frac { 1 }{ 1000 }\) kg = 0.001 kg
2650 g = 2000 g + 650 g
= \(\frac { 2000 }{ 1000 }\) kg + \(\frac { 650 }{ 1000 }\) kg
= 2 kg + 0.650 kg
= 2.650 kg
We can add decimals in the same way as whole numbers.
Subtraction of decimals can be carried out by subtracting hundredths from hundredths, tenths from tenths, ones from ones and so on.

