CBSE Class 7 Maths Notes Chapter 7 Congruence of Triangles
If two figures have exactly the same shape and size, then they are said to be congruent.
For congruence, we use the symbol ‘=’
Two plane figures are congruent, if each when superposed on the other covers it exactly.
e.g. F1 and F2 are congruent if the trace copy of F1 fits exactly on that F2. We can write this as F1 = F2
Two line segments, \(\bar { AB }\) and \(\bar { CD }\) are congruent if they have equal lengths. We can write this as \(\bar { AB }\) = \(\bar { CD }\). However, it is common to write it as \(\bar { AB }\) = \(\bar { CD }\).

Two angles ∠ABC and ∠PQR, are congruent if their measures are equal. We can write this as ∠ABC = ∠PQR or m∠ABC = m∠PQR. Also, it is common to write it as ∠ABC = ∠PQR.
SSS Congruence of two triangles: Two triangles are congruent if the three sides of the one are equal to the three corresponding sides of the other.
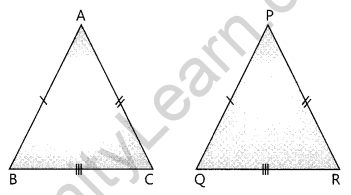
where, AB = PQ, AC = PR, BC = QR
SAS Congruence of two triangles: Two triangles are congruent if two sides and the angle included between them in one of the triangles are equal to the corresponding sides and the angle included between them of the other triangle.
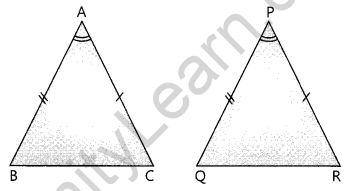
where, AB = PQ, AC = PR, ∠BAC = ∠QPR.
ASA congruence of two triangles: Two triangles are congruent if two angles and the side included between them in one of the triangles are equal to the corresponding angles and the side included between them of the other triangle.
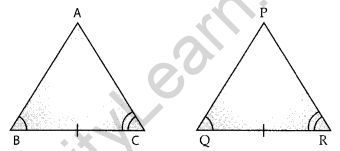
where, BC = QR, ∠ABC = ∠PQR, ∠ACB = ∠PRQ.
RHS Congruence of two right-angled triangles: Two right-angled triangles are congruent if the hypotenuse and a leg of one of the triangles are equal to the hypotenuse and the corresponding leg of the other triangle.
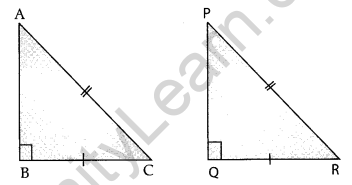
where, AC = PR, BC = QR, ∠ABC = ∠PQR = 90°.
Congruence of Plane Figures
Two figures F1 and F2 are said to be congruent if they cover each other completely.
In this case, we write F1 = F2.
Congruence Among Line Segments
If two line segments have the same (i.e., equal) length, they are congruent. Conversely, if two line segments are congruent, they have the same length.
Line segments are congruent ⇔ their lengths are the same
If line segment AB is congruent to line segment CD, then we write AB = CD
Sometimes we also write AB = CD
and simply say that the line segments AB and CD are equal.
![]()
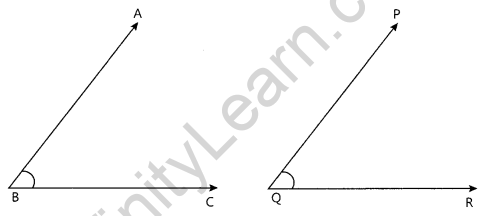
Congruence of Angles
If two angles have the same measure, they are congruent.
Conversely, if two angles are congruent, their measures are the same.
Angles congruent ⇔ Angle measures same
If ∠ABC is congruent to ∠XYZ, then we write ∠ABC = ∠XYZ or m∠ABC = m∠XYZ
where m stands for the measure.
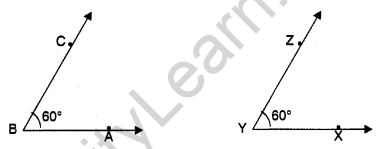
In the above case, the measure is 60°.
Congruence of Triangles
“Two triangles are congruent if they are copies of each other and when superposed, they cover each other exactly.”
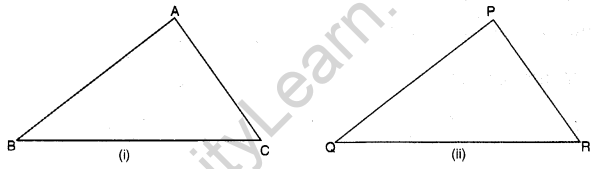
∆ABC and ∆PQR have the same size and shape. They are congruent. So we would express this as ∆ABC = ∆PQR.
This means that, when we place ∆PQR on ∆ABC, P falls on A, Q falls on B and R falls on C, also \(\bar { PQ }\) falls along \(\bar { AB }\), \(\bar { QR }\) falls along \(\bar { BC }\) and \(\bar { PR }\) falls along \(\bar { AC }\).
If under a given correspondence, two triangles are congruent, then their corresponding parts (i.e. angles and sides) that match one another are equal. Thus in these two congruent triangles, we have:
Corresponding vertices: A and P, B and Q; C and R.
Corresponding sides: \(\bar { AB }\) and \(\bar { PQ }\), \(\bar { BC }\) and \(\bar { QR }\); \(\bar { AC }\) and \(\bar { PR }\).
Corresponding angles: ∠A and ∠P, ∠B and ∠Q; ∠C and ∠R.
While talking about the congruence of triangles, not only the measures of angles and lengths of sides matter, but also the matching of vertices. In the above case, the correspondence is A ↔ P, B ↔ Q, C ↔ R
We may write this as ABC ↔ PQR
Criteria for Congruence of Triangles
SSS Congruence Criterion
If under a given correspondence, the three sides of one triangle are respectively equal to the three sides of another triangle, then the triangles are congruent.
SAS Congruence Criterion
If under a corresponding two sides and the angle included between them of a triangle are respectively equal to two sides and the angle included between them of another triangle, then the triangles are congruent.
ASA Congruence Criterion
If under a correspondence two angles and the included side of a triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
Note: If two angles of a triangle are given, we can always find the third angle of the triangle. So, if, two angles and one side of one triangle are equal to the two angles and the corresponding side of another triangle, then the third angle of the two triangles shall also be equal (as the sum of the three angles of a triangle is 180°), so we may convert it into “two angles and the included side” form of congruence and then apply the ASA congruence rule.
Congruence Among Right-Angled Triangles
RHS Congruence Criterion
If under a correspondence, the hypotenuse and one side of a right-angled triangle are respectively equal to the hypotenuse and one side of another right-angled triangle, then the triangles are congruent.
We call this “RHS” congruence because R stands for Right-angle, H stands for Hypotenuse and S stands for Side.
We hope the given CBSE Class 7 Maths Notes Chapter 7 Congruence of Triangles Pdf free download will help you. If you have any query regarding NCERT Class 7 Maths Notes Chapter 7 Congruence of Triangles, drop a comment below and we will get back to you at the earliest.

