Table of Contents
CBSE Class 10 Maths Real Numbers Formulas to solve the problems easily to score more marks in your CBSE Class 10 Board Exam. Class 10 form the basis of solving all problems in some of the toughest competitive exams.
Book: National Council of Educational Research and Training (NCERT)
Class: 10th Class
Subject: Maths
Chapter Name: Real Numbers
CBSE Class 10 Maths Real Numbers Formulas
| S. No | Type of Numbers | Description |
| 1 | Natural Numbers | N = {1,2,3,4,5 > It is the counting numbers |
| 2 | Whole number | W= {0,1,2,3,4,5> It is the counting numbers + zero |
| 3 | Integers | All whole numbers including Negative number + Positive number ……-4,-3,-2,-1,0,1,2,3,4,5… so on. Like whole numbers, integers don’t include fractions or decimals. |
| 4 | Positive integers | Z+ = 1,2,3,4,5, …… |
| 5 | Negative integers | Z– = -1,-2,-3,-4,-5, …… |
| 6 | Rational Number | A number is called rational if it can be expressed in the form p/q where p and q are integers (q> 0). Ex: P/q, 4/5 |
| 7 | Irrational Number | A number is called rational if it cannot be expressed in the form p/q where p and q are integers (q> 0). Ex: √2, Pi, … etc |
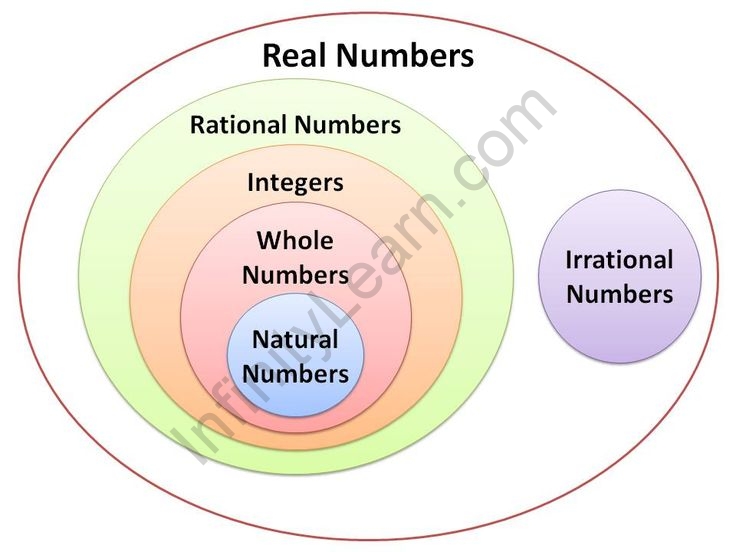
| 8 | Real Numbers | A real number is a number that can be found on the number line. Real Numbers are the numbers that we normally use and apply in real-world applications. Real Numbers include Natural Numbers, Whole Numbers, Integers, Fractions, Rational Numbers and Irrational Numbers |
Euclid’s Division Lemma | CBSE Class 10 Maths Real Numbers Formulas
Euclid’s Division Lemma is defined as “for a given positive integer a and b, there exist unique integers q and r satisfying [a=bq+r,0≤r<b]. An example is given below which will explain this concept better.

HCF (Highest common factor) | CBSE Class 10 Maths Real Numbers Formulas
HCF of two positive integers can be find using the Euclid’s Division Lemma algorithm
We know that for any two integers a. b. we can write following expression
a=bq + r , 0≤r<b
If r=0 .then
HCF( a. b) =b
If r≠0 , then
HCF ( a. b) = HCF ( b.r)
Again expressing the integer b.r in Euclid’s Division Lemma, we get
b=pr + r1
HCF ( b,r)=HCF (r,r1)
Similarly successive Euclid’s division can be written until we get the remainder zero, the divisor at that point is called the HCF of the a and b
-
HCF (a,b) =1 – Then a and b are co primes.
-
Product of primes Theorem of Arithmetic – Composite Number = Product of Primes
-
HCF and LCM by prime factorization method:
HCF = Product of the smallest power of each common factor in the numbers
LCM = Product of the greatest power of each prime factor involved in the number -
Important Formula HCF (a,b) X LCM (a,b) =a X b
-
Important concept for rational Number – Terminating decimal expression can be written in the form p/2n5m
The Fundamental Theorem of Arithmetic | CBSE Class 10 Maths Real Numbers Formulas
This theorem states that “every composite number can be expressed (factorized) as a product of primes, and this factorization is unique, apart from the order in which the prime factors occur. An example includes 36 which can be written as 22×32

We hope that our CBSE Class 10 Maths Real Numbers Formulas helped with your studies! If you liked our CBSE Class 10 Maths Formulas, please share this post if you have any queries drop a comment below and we will get back to you at the earliest..



