Moment of Inertia of a Square

The formula for the moment of inertia of a square is:

I = a⁴ / 12

In this case, a = the square section’s sides. This would be the equation for a solid square with its centre of mass along the x-axis.

A square’s diagonal moment of inertia can also be calculated as;

I_x = I_y = a⁴ / 12

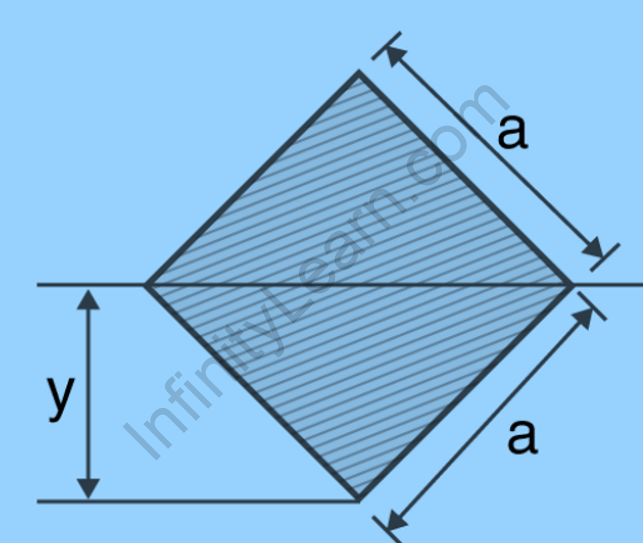
If indeed the centre of mass (cm) is moved to a certain distance (d) from the x-axis, we will use a different expression to calculate the moment of inertia of the same square.

I = a⁴ / 3

Moment of Inertia of a Square Derivation

The parallel axis theorem states that the moment of inertia can be easily calculated.

I = I_cm + Ad²

Icm = centre of mass

Even so, in this lesson, we will replace mass (M) with the area (A). In addition to integration, we will use a rectangle as a reference to find the M.O.I. during the derivation.

Remember that the moment of inertia of a rectangle is given as;

I_X = ⅓ WH³

W = width and H = height

I_X = ⅓ (WH)H²

I_X = ⅓ (A)H²

(1) When we look at the square with its centre of mass passing through the x-axis, we see that it is made up of two equal-sized rectangles.

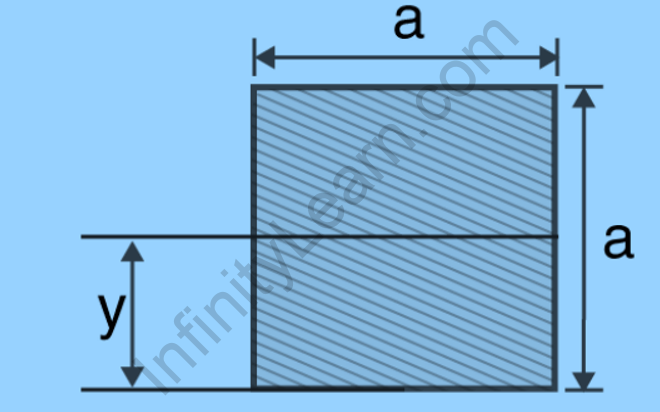
Now, we can express it as;

I_x = 2 [⅓ a (a / 2)³ ]

I_x = [⅔ a ( a³ / 8) ]

I_x = (1/12)a⁴

I_Xcm = a⁴ / 12

(2) The following derivation is for a square when the centre of mass is moved a certain distance (d).

By using the parallel axis theorem we can now state;

I_x = I_cm + Ad²

I_x = (1/12) a⁴ + a² (a / 2)²

I_x = (1/12) a⁴ + (1 / 4) a⁴

I_x = (1/12) a⁴ + (3 / 12) a⁴

I_x = (⅓) a⁴

Moment of Inertia of a Square Plate

A few factors must be considered when calculating the moment of inertia of a square plate.

To begin, we will assume that the plate has mass (M) and length sides (L).

That is, Surface area A = L X L = L²

Now, we will define the mass per unit area as;

That is, Surface density, ρ = M / A = M / L²

By using integration;

I_plate = ∫ dI = ∫ (dI_com + dI_{parallel axis})

I_plate = _x=-L/2∫^x=L/2 (1/12) ρ L³dx + ρ Lx²dx

I_plate = ρ (L³ / 12) [x |_-L/2^L/2 + ρ L [ ⅓ x³ |_-L/2^L/2

I_plate = ρ (L³ / 12) [ L / 2 – (-L / 2)] + ρ L [(⅓ L³ / 8) – (- ⅓ L³ / 8)]

I_plate = ρ (L³ / 12) (L) + ρ L (⅔ L³ / 8)

I_plate = (ρ / 12) L⁴ + (ρ / 12) L⁴

I_plate = (1 / 6) ρ L⁴

I_plate = (1 / 6) (M / L²) L⁴

I_plate = (1 / 6) M L²

FAQs

What is the use of moment of inertia?

The MOI of an entity helps determine how much torque is required to achieve a given angular acceleration. Once calculating torque or rotational force, the mass MOI must be known.

How do we find the Area of a Hollow Square?

Only when P.x is the first moment of area of a specific section, then (Px). X denotes the section's Moment of Inertia (second moment of area). The hollow section's moment of inertia can be calculated by first determining the inertia of a larger rectangle and then subtracting the hollow section from that large rectangle.

Infinity Learn App

Now you can find answers to all your subject queries & prepare for your Exams on our Educational App – Infinity Learn.