Table of Contents
NCERT Solutions for Class 9 Maths Chapter 13 Surface Areas and Volumes include the accurately designed wide range of solved exercise questions for an excellent understanding. These solutions in Maths for Class 9 is prepared considering the latest CBSE syllabus 2023-24 update of Term II examination. NCERT for Class 9 Maths Solutions is mainly created to be a guiding solution and advantageous reference to help students to clear doubts spontaneously and in an effective way. NCERT Solutions for Class 9 Maths is prepared by the teaching faculties having vast teaching experience along with subject matter experts to serve the purpose.
Class 9 NCERT Solutions are developed keeping in mind the concept-based approach along with the precise answering method for Term II examinations. Refer to NCERT Solutions for Class 9 for a better score. It is a detailed and well-structured solution for a good grasp of concept-based knowledge. NCERT for Class 9 Maths Solutions is made available in web and PDF format for ease of access.
Also Check: NCERT Solutions Class 9 Maths Chapter 1 – Number Systems
NCERT Solutions for Class 9 Maths Chapter 13 PDF
In mathematics, there are two main branches of geometry: plane geometry and solid geometry. Plane geometry, also called two-dimensional geometry, deals with flat shapes like squares, triangles, rectangles, and hexagons, focusing on their properties and relationships. On the other hand, solid geometry focuses on three-dimensional objects such as prisms, cylinders, cubes, pyramids, and spheres, exploring their volume, surface area, and other characteristics. For further understanding, you can refer to academic resources like NCERT solutions for Class 10 mathematics, particularly Chapter 13 on Surface Areas and Volumes.
NCERT Solutions for Class 9 Maths Chapter 13 – Surface Areas and Volumes: Download PDF
List of Formulas in NCERT Solutions Class 9 Maths Chapter 13
The study materials provided for Class 10 mathematics include valuable information on various formulas and concepts. It is crucial for students to pay attention to these formulas as they form the foundation of mathematical problem-solving. Each geometric shape has its own unique formula, and it is important for students to differentiate between them to avoid confusion. Some key formulas covered in this chapter are outlined below:
- Surface Area of a Cuboid = 2[(length x breadth) + (breadth x height) + (height x length)]
- Volume of a Cylinder = πr2h
Exercise 13.1 Page No: 213
1. A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is to be open at the top. Ignoring the thickness of the plastic sheet, determine
(I) The area of the sheet required for making the box.
(ii) The cost of the sheet for it, if a sheet measuring 1m2 costs Rs. 20.
Solution:
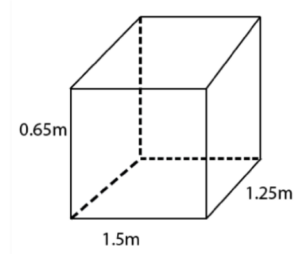
Given: length (l) of box = 1.5m
Breadth (b) of box = 1.25 m
Depth (h) of box = 0.65m
(i) Box is to be open at the top.
Area of sheet required.
= 2lh+2bh+lb
= [2×1.5×0.65+2×1.25×0.65+1.5×1.25]m2
= (1.95+1.625+1.875) m2 = 5.45 m2
(ii) Cost of sheet per m2 area = Rs.20
Cost of sheet of 5.45 m2 area = Rs (5.45×20)
= Rs.109.
2. The length, breadth and height of a room are 5 m, 4 m and 3 m, respectively. Find the cost of whitewashing the walls of the room and ceiling at the rate of Rs 7.50 per m2.
Solution:
Length (l) of room = 5m
Breadth (b) of room = 4m
Height (h) of room = 3m
It can be observed that four walls and the ceiling of the room are to be whitewashed.
Total area to be whitewashed = Area of walls + Area of the ceiling of the room
= 2lh+2bh+lb
= [2×5×3+2×4×3+5×4]
= (30+24+20)
= 74
Area = 74 m2
Also,
Cost of whitewash per m2 area = Rs.7.50 (Given)
Cost of whitewashing 74 m2 area = Rs. (74×7.50)
= Rs. 555
3. The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of Rs.10 per m2 is Rs.15,000, find the height of the hall.
[Hint: Area of the four walls = Lateral surface area.]
Solution:
Let the length, breadth, and height of the rectangular hall be l, b, and h, respectively.
Area of four walls = 2lh+2bh
= 2(l+b)h
Perimeter of the floor of hall = 2(l+b)
= 250 m
Area of four walls = 2(l+b) h = 250h m2
Cost of painting per square metre area = Rs.10
Cost of painting 250h square metre area = Rs (250h×10) = Rs.2500h
However, it is given that the cost of painting the walls is Rs. 15,000.
15000 = 2500h
Or h = 6
Therefore, the height of the hall is 6 m.
4. The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm×10 cm×7.5 cm can be painted out of this container?
Solution:
Total surface area of one brick = 2(lb +bh+lb)
= [2(22.5×10+10×7.5+22.5×7.5)] cm2
= 2(225+75+168.75) cm2
= (2×468.75) cm2
= 937.5 cm2
Let n bricks can be painted out by the paint of the container.
Area of n bricks = (n×937.5) cm2 = 937.5n cm2
As per the given instructions, the area that can be painted by the paint of the container = 9.375 m2 = 93750 cm2
So, we have 93750 = 937.5n
n = 100
Therefore, 100 bricks can be painted out by the paint of the container.
5. A cubical box has each edge 10 cm, and another cuboidal box is 12.5cm long, 10 cm wide, and 8 cm high.
(i) Which box has the greater lateral surface area, and by how much?
(ii) Which box has the smaller total surface area, and by how much?
Solution:
From the question statement, we have
Edge of a cube = 10cm
Length, l = 12.5 cm
Breadth, b = 10cm
Height, h = 8 cm
(i) Find the lateral surface area for both figures.
Lateral surface area of cubical box = 4 (edge)2
= 4(10)2
= 400 cm2 …(1)
Lateral surface area of cuboidal box = 2[lh+bh]
= [2(12.5×8+10×8)]
= (2×180) = 360
Therefore, the lateral surface area of the cuboidal box is 360 cm2. …(2)
From (1) and (2), the lateral surface area of the cubical box is more than the lateral surface area of the cuboidal box. The difference between both lateral surfaces is 40 cm2.
(Lateral surface area of the cubical box – Lateral surface area of cuboidal box=400cm2–360cm2 = 40 cm2)
(ii) Find the total surface area for both figures.
The total surface area of the cubical box = 6(edge)2 = 6(10 cm)2 = 600 cm2…(3)
The total surface area of the cuboidal box
= 2[lh+bh+lb]
= [2(12.5×8+10×8+12.5×100)]
= 610
This implies that the total surface area of the cuboidal box is 610 cm2..(4)
From (3) and (4), the total surface area of the cubical box is smaller than that of the cuboidal box. And their difference is 10cm2.
Therefore, the total surface area of the cubical box is smaller than that of the cuboidal box by 10 cm2
6. A small indoor greenhouse (herbarium) is made entirely of glass panes (including the base) held together with tape. It is 30cm long, 25 cm wide, and 25 cm high.
(i) What is the area of the glass?
(ii)How much tape is needed for all 12 edges?
Solution:
Length greenhouse, say l = 30cm
Breadth greenhouse, say b = 25 cm
Height greenhouse, say h = 25 cm
(i) Total surface area of greenhouse = Area of the glass = 2[lb+lh+bh]
= [2(30×25+30×25+25×25)]
= [2(750+750+625)]
= (2×2125) = 4250
The total surface area of the glass is 4250 cm2
(ii)
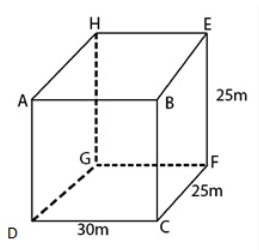
From the figure, the tape is required along sides AB, BC, CD, DA, EF, FG, GH, HE AH, BE, DG, and CF.
Total length of tape = 4(l+b+h)
= [4(30+25+25)] (after substituting the values)
= 320
Therefore, 320 cm tape is required for all 12 edges.
7. Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm×20cm×5cm, and the smaller of dimension 15cm×12cm×5cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is Rs. 4 for 1000 cm2, find the cost of cardboard required for supplying 250 boxes of each kind.
Solution:
Let l, b and h be the length, breadth and height of the box.
Bigger Box
l = 25cm
b = 20 cm
h = 5 cm
Total surface area of bigger box = 2(lb+lh+bh)
= [2(25×20+25×5+20×5)]
= [2(500+125+100)]
= 1450 cm2
Extra area required for overlapping 1450×5/100 cm2
= 72.5 cm2
While considering all overlaps, the total surface area of the bigger box.
= (1450+72.5) cm2 = 1522.5 cm2
Area of cardboard sheet required for 250 such bigger boxes
= (1522.5×250) cm2 = 380625 cm2
Smaller Box
Similarly, total surface area of the smaller box = [2(15×12+15×5+12×5)] cm2
= [2(180+75+60)] cm2
= (2×315) cm2
= 630 cm2
Therefore, the extra area required for overlapping 630×5/100 cm2 = 31.5 cm2
The total surface area of 1 smaller box while considering all overlaps
= (630+31.5) cm2 = 661.5 cm2
Area of cardboard sheet required for 250 smaller boxes = (250×661.5) cm2 = 165375 cm2
In Short
| Box | Dimensions (in cm) | Total surface area (in cm2 ) | Extra area required for overlapping (in cm2) | Total surface area for all overlaps (in cm 2) | Area for 250 such boxes (in cm2) |
| Bigger Box | l = 25b = 20
c = 5 |
1450 | 1450×5/100= 72.5 | (1450+72.5) = 1522.5 | (1522.5×250) = 380625 |
| Smaller Box | l = 15b = 12
h =5 |
630 | 630×5/100 = 31.5 | (630+31.5) = 661.5 | ( 250×661.5) = 165375 |
Now, total cardboard sheet required = (380625+165375) cm2
= 546000 cm2
Given, cost of 1000 cm2 cardboard sheet = Rs. 4
Therefore, the cost of 546000 cm2 cardboard sheet =Rs. (546000×4)/1000 = Rs. 2184
Therefore, the cost of cardboard required for supplying 250 boxes of each kind will be Rs. 2,184.
8. Praveen wanted to make a temporary shelter for her car by making a box-like structure with a tarpaulin that covers all four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small and therefore negligible, how many tarpaulins would be required to make the shelter of height 2.5m, with base dimensions 4m×3m?
Solution:
Let l, b and h be the length, breadth and height of the shelter.
Given:
l = 4m
b = 3m
h = 2.5m
Tarpaulins will be required for the top and four wall sides of the shelter.
Using formula, area of tarpaulin required = 2(lh+bh)+lb
On putting the values of l, b and h, we get
= [2(4×2.5+3×2.5)+4×3] m2
= [2(10+7.5)+12]m2
= 47m2
Therefore, 47 m2 of tarpaulin will be required.







