Laws of Motion

Laws of Motion

What make things move or stop? What rules govern their motion? Well, at the first glance, it may seem to be an absurd question. Even a child knows that when he/she pulls the thread attached to a toy, the toy starts moving. Then why the fuss about Laws of motion!!

Well, it turns out that things are not that easy. Certainly not! In fact they are counter-intuitive, as you will soon see!

Aristotle’s view about motion

Two main efforts were made by western scientists in last 2300 years to study basics of motion.

Aristotle (384 B.C. – 322 B.C) was of the opinion that every body has its preferred state of motion as rest. Moving things prefer to come to rest and bodies at rest wish to remain at rest. This was Aristotle’s view. He said that if you see a body moving because there is some force acting non-stop on the body.

To keep things moving, a force is needed. On their own, they come to rest.

Aristotle seems to be quite right. Suppose you slide a coin against the floor, you see that it comes to halt, at some time. In day-to-day lives, moving bodies come to a halt. Coin came to rest because coin wanted (as Aristotle thought) to come to rest.

For long this view of Aristotle was held regarding motion of bodies, for a good 1600 years, before this man, known as a great of physics, Sir Issac Newton (shown in picture) came up with clear-cut laws for motion, now known after his name.

Newton’s view about motion

Newton’s view of motion brought Aristotlean view upside down. Newton said that preferred state of motion for a body is not necessarily rest but it is the state of motion in which the body finds itself currently in. If a body is at rest at this instant, it wishes to be at rest. On the other hand, if a body is moving at this instant with a speed of 1ms-1 towards west, then it wishes to keep moving like that. So, any state of motion is a preferred state for a body if a body possesses it. Rest is not the preferred state, in general.

So, you see, Newton’s view is very different from Aristotle’s! Rest has no special significance for Newton whereas it was very special state of motion for Aristotle.

Math Formulas Math Articles Ohm’s Law Kirchhoffs Laws

Newton’s laws of motion

Newton formalized three laws that govern how things move.

• Newtons’ First law of motion (Law of inertia)

As described earlier, Newton emphasized that any body wishes to hold on to that state of motion that it finds itself currently in. Newton termed this tendency of any body as inertia. Inertia, as you know, means laziness, tendency to not change, resisting any change.

Formally, the first law is stated as: Every body continuous to be in a state of rest or of uniform motion in a straight line, unless it is acted upon by an unbalanced external force.

Statement of the first law emphasizes on inertia as inherent property possessed by every body. Bodies resist change to their current state of motion. Another physical quantity that the first law introduces is the force. Newton said that by applying a force, a body can be made to change its state of motion, or, in other words, we can overcome inertia of the body.

So we have two terms mentioned in first law:

Inertia – It is a property of a body by virtue of which it develops tendency not to change its state of motion on its own.

Force – It is an agency that changes the state of motion

You never see a car changing its speed on its own from 40kmph to 50 kmph. It possesses inertia. But we can change the speed of the car from 40kmph to 50 kmph by applying an external force.

In summary,

• Bodies possess inertia
• But you can overcome inertia by applying unbalanced force on the body

Mass a measure of inertia: Experimentally, it is found that the greater the mass of the body, the greater is the inertia (resistive power). A 10 g marble resists you less than a 100 kg box, when both are kept on a nice, smooth floor, and you are trying to make them reach speed of 1 metre per second. A relatively much larger force is required on the box than on the marble because box has larger resistance (as well as mass).

Need for external force: By sitting inside a stationary car, you become the car itself. Now by pulling on to the car or pushing on to it, you cannot make it to move. You have to be external to the car, then apply a force on the car, to make it move.

Problem 1

A truck and a pebble both possess inertia. Are their inertia of same magnitude?

Solution:

No. Inertia is proportional to mass. The greater the mass, the greater is the inertia.

Newtons’ second law of motion

The second law establishes a mathematical relationship between the applied external force on the object and its resulting change in momentum.

First let us define momentum.

Momentum: It is defined as product of mass times velocity.

When you apply force on a body, assuming its mass remains constant, which is generally the case, you change its velocity. And hence you change its momentum.

Newton said due to the force body’s momentum changes; how fast it changes depends on the amount of external force. The greater the external force the more rapid is the momentum change.

Statement of second law: The rate of change of momentum of a body is directly proportional to the external force acting on it and it takes place in the direction of the force.

If F is the external force, P is the initial momentum of the body and dp is the change in momentum in a small interval of time dt, then

F ∝ dp/dt⟹ k x dp/dt, where k is a constant of proportionality.

In fact, we use, F ∝ dp/dt , by making k =1

When momentum is P, let velocity of the body be v

When momentum is p+dp, let velocity of the body be v+dv

So, p=mv, p+dp=m(v+dv)

So,

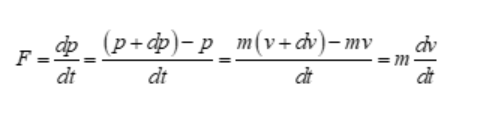
But dv/dt acceleration.

Acceleration and force point in the same direction.

Problem 2:

Which possesses greater momentum – a 1000 kg car moving with a speed of 10ms-1 or a 150kg motorcycle moving with a speed of 80ms-1?

Solution:

P_car = m_carv_car = (1000)(10) = 10¹⁴kgms^-1
P_mc = m_mcv_mc = (150)(80) = 1.2 x 10⁴kgms^-1

Motorcycle possesses greater momentum.

Problem 3:

A force F acting on a heavy body changes its momentum by a certain amount in time t. How much time, will the same force take to change the momentum of a body, having half the mass, by the same amount?

Solution:

F = Δp/Δt ⟹ Δt = Δp/F

Since, Δp and F are same, time required is same.

Problem 4:

For the same duration, a force is applied on two objects, initially at rest. Finally which object has greater speed – heavier or lighter?

Solution:

F = Δp/Δt ⟹ mv – mu = FΔt

⟹ mv – 0 =FΔt
⟹ v = FΔt/m ∝ 1/m

Lighter object has greater speed. Note both possess same momentum, though.

Newtons’ third law of motion

This law is the most popular and it tells about forces acting on bodies.

Statement of third law: To every action, there is an equal and opposite reaction.

• We should understand some aspects/points of this law.
• To apply a force on a body, say A, you need another body, say B
• If F is the force applied by body B on body A at a given instant, then at the same instant, body A must also be applying a force of the same magnitude but opposite in direction, on body B.
• Essentially A and B receive one force each and they apply one force each, on one another.
• Two forces act on two different bodies.
• A body does not apply a force on itself.
• These two forces form action-reaction pair – with either one can be called as action or a reaction.
• Forces are always even in number in nature.

Examples

• 
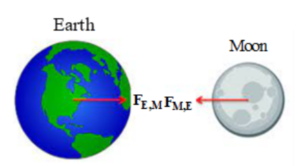
• Earth applies gravitational force on Moon (FM,E pointing from Moon towards Earth). Moon also applies gravitational force on Earth – of same magnitude but opposite in direction (FE,M pointing from Earth towards Moon).
• 
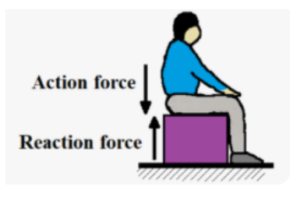
• We sit on a chair. We push the chair down with a force of magnitude, say, F. Chair pushes us up with a force of magnitude, F.

Problem 5

A book rests on a table. It is pulled downwards by the gravitational force of the Earth. What of the following is the reaction force of this force?

1. The gravitational force applied by the book on the Earth in the downward direction
2. The gravitational force applied by the book on the Earth in the upward direction
3. The force applied by the table on the book in the downward direction
4. The force applied by the table on the book in the upward direction

Solution:

For discussing action-reaction between book and table, third body (here, table) should not be thought about. Book is pulled down by the Earth. Its reaction force is: Earth is pulled up by the book.

Frequently Asked Questions on Laws of motion

Who first gave correct description regarding motion of bodies?

Newton discovered the laws governing motion of bodies.

What does inertia mean?

The property of a body by virtue of which it resists change in its state of motion is called inertia.

What is meant by momentum?

Momentum is defined as product of mass and velocity.

Which law of motion gives quantitative relationship between force and motion of a body?

Newton’s second law of motion gives equation F=ma which tells what acceleration a will a body of mass m receive when a force F acts on it.

When a ball and Earth pull each other by the same force why don’t we see the Earth moving?

By Newton’s second law, a = F/m. The value of F is same for both Earth and ball. But mass of Earth is extremely large. Hence its acceleration is relatively extremely less.