Table of Contents
Louis de Broglie presented his research thesis in 1924, in which he proposed that electrons, like light, have properties of both waves and particles. He rearranged the terms of the Plank-Einstein relation to be applied to all types of matter.The de Broglie equation is an equation used to describe the wave properties of matter, specifically the electron’s wave nature:
λ = h/mv,
Where λ is the wavelength, h is Planck’s constant, and m is the mass of a particle moving at a constant velocity. De Broglie proposed that particles can have wave-like properties.The de Broglie hypothesiswas confirmed when matter waves were observed in George Paget Thomson’s cathode ray diffraction experiment and the Davisson-Germer experiment applied to electrons. Since then, it has been demonstrated that the de Broglie equation applies to elementary particles, neutral atoms, and molecules.According to the de Broglie equation, matter can behave like waves in the same way light and radiation do. The equation explains that a beam of electrons can be diffracted like a beam of light. The de Broglie equation clarifies the concept of matter having a wavelength. As a result, every moving particle, whether microscopic or macroscopic, will have a wavelength. The wave nature of matter can be detected or is visible in macroscopic objects.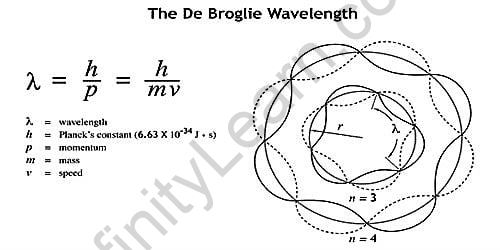 
de Broglie Equation
The de Broglie equation is one of the equations commonly used to define the wave properties of matter. It describes the electron’s wave nature. Electromagnetic radiation has the dual nature of a particle (with momentum) and a wave (expressed in frequency and wavelength). Microscopic particle-like electrons also demonstrated this dual nature property. In his thesis, Louis de Broglie proposed that any moving particle, whether microscopic or macroscopic, will be associated with a wave character.It was called ‘Matter Waves.’, He also proposed a relationship between a particle’s velocity and momentum and its wavelength if the particle had to behave like a wave.
De Broglie Equation Derivation and de Broglie Wavelength
Particles of very low mass moving at less than the speed of light behave like a particle and a wave. De Broglie developed an expression that relates the mass of such smaller particles to their wavelength. According to Plank’s quantum theory, the energy of an electromagnetic wave is proportional to its wavelength or frequency.
As E = mc2…….., Einstein related the energy of particle matter to its mass and velocity (2) Because the smaller particle has a dual nature and the same energy, de Broglie equated both of these relations for the particle moving with velocity ‘v’ as,
This equation relating a particle’s momentum to its wavelength is known as the de Broglie equation, and the wavelength calculated using this relation is known as the de Broglie wavelength.
- De Broglie Hypothesis_Chemistry
- De Broglie Wavelength
- De Broglie’s Relationship
- Important Topic Of Physics De Broglie Relation
FAQ’s on De broglie equation
Is the De Broglie equation applicable to electrons?
Yes, this equation applies to every moving body in the universe, right down to the atomic level. Light particles, such as photons, have their wavelengths, which is true for electrons. It has wave-particle duality only when the equation treats electrons as both waves and particles. This is true for every electron in every atom of every element. The wavelength of an electron can be calculated using the equation mentioned.
What is the significance of the de Broglie relationship?
De Broglie proposed that, just as light has wave-like and particle-like properties, the matter has wave-like and particle-like properties as well. This nature was described as dual matter behaviour. De Broglie derived a relationship between wavelength and matter momentum based on his observations.
