Table of Contents
De Broglie Wavelength Formula
De Broglie wavelength formula: What is De Broglie wavelength and what is its significance? Let us find out answers to these questions in this article that exclusively talks about De Broglie wavelength formula.
De Broglie determines the probability density of finding an object at a given point in the configuration space. If the wavelength of the de Broglie particle is small compared to the characteristic size that determines the given problem conditions, the system’s behavior is close to the classical one. If a particle is significantly larger than its de Broglie wavelength, or if it interacts with other objects on a scale significantly larger than its de Broglie wavelength, its wave properties are not obvious. The wave nature of matter can only be observed for very small objects, and the de Broglie wavelength in the double-slit interference model is created using electrons as the source.
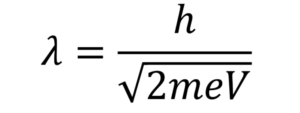
De Broglie Wavelength Formula assumes that:
All matter has wave properties and relates the observed wavelength of matter to its momentum. In his 1924 doctoral dissertation, De Broglie suggested that just as light has both wave and particle properties, electrons also have wave properties. The wave nature of electrons has also been experimentally found to support this assumption. Physicist Louis de Broglie suggested that particles could have both wave and particle properties.
“Louis de Broglie assumed the wave nature of particles through a series of substitutions.”
Louis de Broglie (1892-1987) developed a formula related to this double wave and particle behavior. French physicist Louis de Broglie was able to solve mathematical problems by linking Einstein’s mass-energy equivalence equation (E=mc2) with Planck’s equation (E=hf) and the wave velocity equation (v=lf). To determine what the electron’s wavelength should be and replace the momentum of the series, look at De Broglie Wavelength Formula; as the electron’s velocity decreases, the electron’s wavelength increases.
Using a velocity of 3.00 x 108 m/s, calculate the electron’s wavelength. This formula relates the wavelength to the momentum of the wave/particle. The relationship is that the wavelength is h, Planck’s constant, divided by p, the particle’s momentum. The integrand p(x) is just the classical momentum of the particle, expressed as a function of coordinates.
Mass times kinetic energy is half m2 squared, half mv squared, and half the square of our electron’s momentum. The first thing that comes to mind is the de Broglie relation, which relates the wavelength of a particle to its momentum and its particle. In this case, the excitation energy of electrons does not reach their rest energy since this is required to describe the de Broglie wavelength during the translational motion of particles. In this case, the electron energy in the field of the nucleus changes, the photon energy is emitted, the angular momentum of the electrons increases, and the de Broglie wavelength decreases.
Let’s define the main feature related to wave-particle duality:
Suppose the energy of a standing wave inside a particle reaches the rest energy of those particles. In that case, the de Broglie wavelength is calculated the same way as the photon’s wavelength in the particle—corresponding impulse. Because the de Broglie wavelength behaves like the wavelength of a photon with the related momentum of the combined particle and wave, the de Broglie wavelength is considered a probability wave associated with a d’ function wave. For physicists, this idea is important because it means that any particle can have wave properties. Still, the wave equation can also describe phenomena in the matter if de Broglie wavelengths are used. De Broglie Wavelength Formula suggests that wave-particle duality is not just an anomalous behavior of light but a fundamental principle exhibited by both radiation and matter.
Matter waves were first experimentally confirmed in George Paget Thomson’s experiment on electron beam diffraction [2] and the Davisson-Germer experiment for electrons. De Broglie’s hypothesis was confirmed for other elementary particles. A step forward in comparison with Louis de Broglie is made by theories that in quantum mechanics exclude the concept of a classical point particle and explain the observed facts only with the help of wave packets of matter waves. We will talk about a single particle in an external field for simplicity. The wave nature of electron particles is used in the electron microscope.
Light particles, like electrons, reach speeds of the order of the speed of light faster, become relativistic, and exhibit quantum and wave properties at low energies. However, objects of everyday experience have a calculated wavelength much shorter than that of electrons, so their wave properties have never been discovered; familiar objects show only the behavior of the particles. All particles with measurable wavelengths are very small.
The de Broglie hypothesis can predict the wavelength of matter of any size, and there are practical limits to when it can be useful. The de Broglie wavelength shows an inverse relationship between linear momentum and wavelength (i.e., particles with high momentum have short wavelengths).
De Broglie believed that, at the macroscale, particles have such a large momentum that their wavelengths cannot be detected. Since real particles do not move at the speed of light, Louis de Broglie subordinated the speed (\(v\)) to the speed of light (\(c\)). De Broglie argued that a periodic phenomenon appears to be in phase with a wave of wavelength and frequency that propagates with phase velocity to a stationary observer.
Based on the equation E = hv, the electron wave frequencies mean that electrons can only exist in an atom at certain energies, as previously theorized by Bohr.
FAQs:
What is the de Broglie wavelength formula?
λ = h/mv
What is the de Broglie wavelength of the electron?
The wavelength associated with the electron having a mass and momentum.
The wavelength associated with the electron having a mass and momentum?
Determines the probability density of finding the object at a given point of the configuration space.
Infinity Learn App
Now you can find answers to all your subject queries & prepare for your Exams on our Educational App – Infinity Learn.






