Table of Contents
Dimensions of Volume: Dimension in math and science does not have a specific dimensional formula. The dimension of any phy
sical quantity is the power to which the basic units are raised to obtain one unit of that quantity. The dimensional formula of every quantity is the expression that shows the powers to which fundamental units must be raised in order to obtain one unit of a derived quantity.
Dimensions of Volume
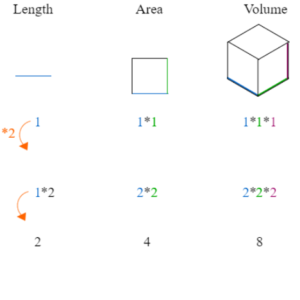
A volume would be simply the amount of space taken up by any three-dimensional solid. A cube, a cuboid, a cone, a cylinder, or a sphere are examples of solids. A solid’s volume is calculated in cubic units. For instance, if the dimensions are given in metres, the volume will be given in cubic metres. That’s the International System of Units’ standard volume unit (SI). Other volume units include cubic centimetres, cubic feet, cubic inches, and so on. The volume of a container can be defined as the total capacity or amount that it can hold. For example, the amount of fluid, gas, or liquid that the container can hold. The volume, however, cannot be specified for the amount of space that the container occupies.
Arithmetically, shapes with a three-dimensional structure are recognised to have volume. Volume can be represented in a simple way for the space required for certain shapes such as straight-edged, regular, and circular shapes. Using arithmetic formulas, these shapes can be easily identified.
We could also calculate the volumes of solids that do not have a well-known regular shape. If there really is a formula for the shape’s boundary, it can be done using integral calculus.
Dimensional Formula of Volume
The volume of something like a three-dimensional structure indicates the total space occupied by the same structure.
It is known that, Length x Breadth x Height = Volume
Volume can be written as,
L x L x L = L³
So, Dimensional formula of volume = [M° L³ T°]
And m³ = SI unit of Volume
Derivation
We have seen, Length × breadth × height = Volume (V) ——- (1)
[M° L¹ T°] = the dimensional formula of length —— (2)When we substitute the equation (2) in equation (1) we will get,
Volume = Length × breadth × height
That is, V = [M° L¹ T°] × [M° L¹ T°] × [M° L¹ T°] = [M° L³ T°]
Thus, we conclude that dimensionally [M° L³ T°] is represented for the volume.
FAQs
Q. What is the dimensional formula of volume?
Ans: Volume has been represented dimensionally as [M° L³ T°].
Q. Is dimension the same as volume?
Ans: The distinction between volume and dimension as nouns is that volume is a three-dimensional measure of space that consists of a length, width, and height and is measured in units of cubic centimetres in metric, cubic inches or cubic feet in English measurement, whereas dimension is dimension.
Q. How to create a dimensional formula?
Ans: Only when Q is the unit of a derived quantity represented by Q = MaLbTc, then MaLbTc is referred to as the dimensional formula, and the exponents a, b, and c are referred to as the dimensions.
