Table of Contents
Before we look at the Centre of mass formulas allows us rapidly to take a gander at what the idea implies. Centre of mass of a body is characterized as a place where entire of the mass of the body gives off an impression of being concentrated.
What is the Center of Mass?
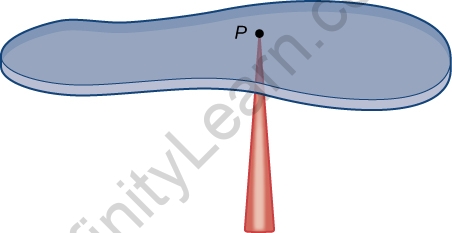
- Centre of mass of a body or arrangement of a molecule is characterized as, a place where the entire of the mass of the body or every one of the masses of an arrangement of molecule seemed, by all accounts, to be concentrated. In material science, we can say that the focal point of mass is a point at the focal point of the circulation of mass in space (otherwise called balance point) wherein the weighted relative place of the conveyed mass has an amount of nothing. In straightforward words, the focal point of mass is a place that is comparative with an item. We can say that it is the normal place of the relative multitude of parts of the framework or it is the mean area of circulation of mass in space. It is where power is normally applied that outcomes in direct speed increase with next to no precise speed increase.
- Whenever we are concentrating on the elements of the movement of the arrangement of a molecule in general, then, at that point, we want not make a big deal about the elements of individual particles of the framework. In any case, just spotlight on the dynamic of an extraordinary point compared to that framework.
- Movement of this remarkable point is indistinguishable from the movement of a solitary molecule whose mass is equivalent to the amount of all singular particles of the framework and the resultant of the relative multitude of powers applied on every one of the particles of the framework by encompassing bodies (or) activity of a field of power is applied straightforwardly to that molecule. This point is known as the focal point of mass of the arrangement of particles. The idea of focus of mass (COM) is valuable in breaking down the convoluted movement of the arrangement of articles, especially when two and more items impact or an article detonates into parts.
Centre of Mass Formulas
- An arrangement of two point masses m1r1 = m2r2. The Centre of mass lies nearer to the heavier mass.
- Triangle (at the centroid) – yc=h/3
- A semi-circular disc – yc= 4r/3π
- Semicircular ring – yc= 2r/π
- Hemispherical shell – yc= r/2
- Solid Hemisphere – yc =3r/8
- Cone – The height of the centre of mass from the base is h/4 for the solid cone and h/3 for the hollow cone.
Watch Session on Our YT Channel
Motion of the Center of Mass and Conservation of Momentum
1. Velocity of Centre of mass
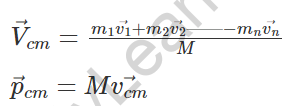
2. Acceleration of centre of mass
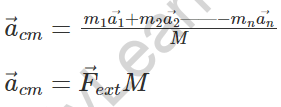
Impulse
Collision
- Momentum conservation m1v1+m2v2 =m1v’1 + m2v’2
- Elastic Collision= ½ m1v12 + ½ m2v22 = ½ m1v’1 2+½m2v’22
- Coefficient of restitution
- e=0, completely elastic collision
- e=1, completely inelastic collision
- If v2=0 and m1≪ m2 then v’1 = -v1
- If v2=0 and m1 ≫ m2 then v’2 = 2v1
- Elastic Collision with m1=m2 then v’1 = v2 and v’2 = v1
Watch Session on Our YT Channel
Centre of Gravity
The Center of gravity can be taken as the point through which the power of gravity follows up on an item or framework. It is essentially direct around which the resultant force due toward gravity powers vanishes. In situations where the gravitational field is thought to be uniform the focal point of gravity and focus of mass will be something very similar. Here and there these two terms – the focus of gravity and centre of mass are utilized conversely as they are often supposed to be at a similar position or area.
System of Particles
- The term system of particles implies a distinct assortment of countless particles that could conceivably associate with one another or are associated with one another. They might be genuine particles of unbending bodies in translational movement. The molecule which associates with one another apply force on one another.
- Between a couple of ith and jth molecule. These powers of common connection between the molecule of the framework are known as the inward power of the framework.
- These inward powers generally exist two by two of equivalent size and inverse headings. Other than inward powers outer powers may likewise follow up on all or a portion of the particles. Here the term outer power implies a power that is following up on anyone molecule, which is remembered for the framework by another body outside the framework.
What is a Rigid body?
- Practically speaking, we manage broadened bodies, which might be deformable or non-deformable (or) unbending. A lengthy body is additionally an arrangement of a vastly huge number of particles having a boundlessly little division between them. Whenever a body disfigures, the division between the distance between its particles and their general areas changes. An unbending body is a drawn-out object where the divisions and relative area of every one of its constituent particles continue as before under all conditions.
- It is the normal place of the multitude of parts of the framework, weighted by their masses. For a basic inflexible article that has a uniform thickness, the focal point of mass is situated at the centroid.
Determining the Center of Mass
- In the event that we were to tentatively decide a body’s focal point of mass, we can utilize gravity powers on the body to do as such. This should be possible essentially as a result of the way that the focal point of mass is equivalent to the focal point of gravity in the equal gravity field close to the world’s surface. Additionally, the focal point of mass of a body with a pivot of evenness and steady thickness will lie on this hub. Similarly, the focal point of mass of a round chamber having steady thickness will have its focal point of mass on the pivot of the chamber we talk about a circularly symmetric assortment of consistent thickness then, at that point, its COM is at the focal point of the circle. Assuming we talk about it in an overall setting, for any evenness of a body, its focal point of mass will for the most part be a proper mark of that balance.
Watch JEE Related Session Videos on Our YT Channel
| Title | Links |
| My Jee Preparation Journey: How I cracked IIT | Click Here |
| most important questions and concept of chemistry from high weightage chapters | Click Here |
| NTA Based Full Maths Paper Predictor | Click Here |
| Low Marks in Mocks? Stuck? Here’s How to Increase Your Score | Click Here |
| Full Revision – Mechanics (Linear + Rotational) – must do problems | Click Here |
| JEE Main 2025 | Last 20 Days Strategy to Score 150+ in Jan Attempt | JEE 2025 | Click Here |
| Menti Maths Vs Chemistry: Full Syllabus Mock Test | Click Here |
| Last 10 Days Strategy For Jee Main 2025 Jan Attempt | Click Here |
| NCERT Challenger for JEE Mains 2025 (20 Best Questions of GOC) – Newly framed & Best PYQ | Click Here |
| Test Your Preparation – Gravitation – Challenging Questions for JEE 2025 | Click Here |
| Jee Advanced Questions Important For Jee Main 2025 | Click Here |
| D & F Block in one shot – Newly framed & Best PYQ for JEE Mains 2025 | Click Here |
| Electrostatics – Questions to boost your rank – Part 1 | Click Here |
| Jee 2024 Most Repeated Questions From All 20 Shifts | Click Here |
| Mock test for Complete Inorganic Chemistry – 1 (for JEE Mains 2025) | Click Here |
| Expected Marks Vs Percentile For Jee main 2025 Jan Attempt | Click Here |
| 12 Hours Marathon | Complete Organic Chemistry | Last Minute Revision | Click Here |
| Jee Main 2025 January Attempt Paper Prediction | Click Here |
| Dual Nature of Radiation and Matter | Click Here |
| Which Attempt is Important Jan Or April ? | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 1 | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 2 | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 3 | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 4 | Click Here |
FAQs on Important Centre Of Mass Formulas For JEE
Is centre of mass important for JEE Mains?
Yes, the centre of mass is an important topic for JEE Mains, especially in mechanics. Questions often test formulas, concepts, and problem-solving techniques related to this.
What are the important points of the centre of mass?
The centre of mass is the point where the entire mass of a system is considered concentrated. For symmetrical objects, it lies at the geometric centre; for irregular ones, calculations are needed.
How to remember centre of mass?
Practice problems regularly, focus on visualizing physical systems, and memorize key formulas through repetition and applying them in mock tests or past papers.
What is the rule of centre of mass?
In the event that we push on an inflexible item at its centre of mass, the article will continuously move as though it is a point mass. It won't turn about any hub, no matter what its genuine shape. Assuming the item is exposed to a lopsided power at another point, then, at that point, it will start turning about the centre of mass.
What affects centre of mass?
The accompanying variables influence the focal point of mass: The place of mass from the pivot. The mass of the unbending body. The hub of the framework. The conveyance of mass.
Could the centre of mass be external of an object?
For empty articles or a uniform ring, the centre of mass can be situated external the item. For a ring, centre of mass lies at the centre of the circle made by the ring. For an empty article like the horseshoe, the centre of mass is outside.