Moment of Inertia of a Ring

Moment of Inertia of a Ring: The moment of inertia is really a quantitative measure of a body’s rotational inertia—that is, the resistance that the body exhibits to having its speed of rotation about an axis modified by the application of torque (turning force). The axis can be internal or external, and it can be fixed or not. Even so, the moment of inertia (I) has always been specified in relation to that axis and is defined as the sum of the products obtained by multiplying the mass of every particle of matter in a given body by the square of its distance from the axis. The moment of inertia is analogous to mass in linear momentum when calculating angular momentum for a rigid body. The momentum p of linear momentum seems to be equal to the mass m multiplied by the velocity v, whereas the momentum L of angular momentum is equal to the moment of inertia I multiplied by the angular velocity.

Now, the Moment of Inertia of a ring can be determined using various expressions. It includes;

• Whenever the axis is passing through the centre (z-axis) and is perpendicular to it. For this we use;

I = mR²

• Across the axis which passes through the diameter. For this we have;

I_x = I_y = mR² / 2

We’ll take a closer look at how the equations are created.

We will calculate the moment of inertia of a ring in both cases below.

(1) Initially, consider a ring with an axis passing through the centre.

We would then assume that the ring’s mass is M and its radius is R.

And we need to cut an elemental ring (dx) around the ring’s circumference. As a result, the elemental ring’s mass (dm) will be;

dm = (m / 2πR) dx

Now, we determine dI = (dm) R²

dI = [(m / 2πR) dx]R²

When substituting the values, we get;

dI = (m / 2πR) R² dx

By using integration;

I = (m R/ 2π) _o∫^2πR dx

I = (m / 2π) [x] ₀^2πR

I = (mR/2π) [2πR – 0]

I = mR²

(2) The moment of inertia of a ring about an axis passing through its diameter will be the subject of the second expression.

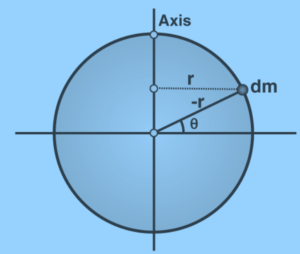
Now, we have to recall the formula;

I = ∫ r′²dm

We need to find dm.

dm = M / 2π dθ

But, r′ = r cos θ

By applying integration, we will have;

I = _o∫^2π r² cos² θ (M / 2π) dθ

I = Mr² / 2π _o∫^2π cos² θ dθ

I = Mr² / 2π [θ / 2 + sin 2 θ / 4] |_o^2π

I = Mr² / 2π [ ( π + 0) – (0 + 0)]

I = Mr² / 2

FAQs

What is the moment of inertia of a ring about a tangent?

The moment of inertia of a ring about its diameter has been known to be MR²/2. As a result, the moment of inertia of a ring about a tangent in the plane of the ring's circle is 3MR²/2.

Determine the moment of inertia of a ring about an axis through its centre perpendicular to its plane.

A uniform ring does have a moment of inertia of 100kgm2 about an axis passing through its centre and perpendicular to its plane.

Also Read: Moment of Inertia of Rectangle | Moment of Inertia of Annular Disc