Table of Contents
In one of our previous articles, we discussed about moment of inertia of a rectangle. In this article, we shall learn about how to calculate the moment of inertia of a solid cylinder. We shall also learn the derivation.
The equation that gives the moment of inertia of a solid cylinder about its centre is:
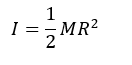
Where M = total mass and R = radius of the cylinder.
Don’t Miss: JEE Main 2025 Paper Analysis (22nd Jan) Shift 1 & Shift 2 | JEE Main 2025 Paper Analysis (23rd Jan) Shift 1 & Shift 2 | JEE Main 2025 Paper Analysis (24th Jan) Shift 1 & Shift 2 | JEE Main 2025 Paper Analysis (28th Jan) Shift 1 & Shift 2 | JEE Main 2025 Paper Analysis (29th Jan) Shift 1 & Shift 2
Derivation of Moment of Inertia of a Solid Cylinder
Initially, we start with a solid cylinder of mass M, radius R, and length L. We’ll figure out its moment of inertia about the central axis.
Several factors must be considered in this case:
- The solid cylinder must be cut or split into extremely thin rings.
- Every ring is made up of the thickness dr and the length L.
- We must sum the moments of these infinitesimally thin cylindrical shells.
We would then take the steps that have been laid out for us.
(1) We’ll use the general moment of inertia equation:
dI = r2 dm
Then, we move on to finding the dm. It is normally given as;
dm = ρ dV
To get dm we have to calculate dv first. It is given as;
dV = dA L
In the meantime, dA is the area of the big ring (radius: r + dr) minus the smaller ring (radius: r). Thus;
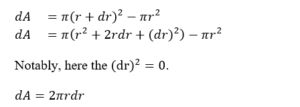
Watch Session on Our YT Channel
(2) When substituting dA into dV we get;
dV = dAL = 2πrdrL
Then, we substitute dV into dm and we will have;
dm = (2πrdr)Lρ
Now, the dm expression is further substituted into the dI equation and we get;
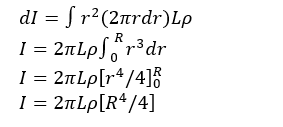
(3) Conversely, we must also find the expression for density. We employ the equation;
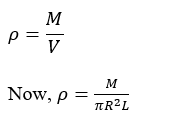
(4) The final stage is to use integration to calculate the moment of inertia of the solid cylinder. The integration takes the shape of a polynomial integral form.
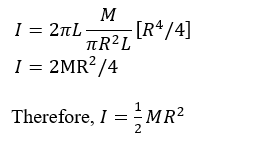
Related Post
- How to Calculate Moment of Inertia
- Moment Of Inertia of A Circle
- Moment of Inertia of Semicircle
- Moment of Inertia of Rectangle
Watch JEE Related Session Videos on Our YT Channel
| Title | Links |
| My Jee Preparation Journey: How I cracked IIT | Click Here |
| most important questions and concept of chemistry from high weightage chapters | Click Here |
| NTA Based Full Maths Paper Predictor | Click Here |
| Low Marks in Mocks? Stuck? Here’s How to Increase Your Score | Click Here |
| Full Revision – Mechanics (Linear + Rotational) – must do problems | Click Here |
| JEE Main 2025 | Last 20 Days Strategy to Score 150+ in Jan Attempt | JEE 2025 | Click Here |
| Menti Maths Vs Chemistry: Full Syllabus Mock Test | Click Here |
| Last 10 Days Strategy For Jee Main 2025 Jan Attempt | Click Here |
| NCERT Challenger for JEE Mains 2025 (20 Best Questions of GOC) – Newly framed & Best PYQ | Click Here |
| Test Your Preparation – Gravitation – Challenging Questions for JEE 2025 | Click Here |
| Jee Advanced Questions Important For Jee Main 2025 | Click Here |
| D & F Block in one shot – Newly framed & Best PYQ for JEE Mains 2025 | Click Here |
| Electrostatics – Questions to boost your rank – Part 1 | Click Here |
| Jee 2024 Most Repeated Questions From All 20 Shifts | Click Here |
| Mock test for Complete Inorganic Chemistry – 1 (for JEE Mains 2025) | Click Here |
| Expected Marks Vs Percentile For Jee main 2025 Jan Attempt | Click Here |
| 12 Hours Marathon | Complete Organic Chemistry | Last Minute Revision | Click Here |
| Jee Main 2025 January Attempt Paper Prediction | Click Here |
| Dual Nature of Radiation and Matter | Click Here |
| Which Attempt is Important Jan Or April ? | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 1 | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 2 | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 3 | Click Here |
| 300 Most Expected JEE Mains 2025 Questions |Non Stop 6 Hours Marathon | Paper Predictor | Part 4 | Click Here |
Moment of Inertia of a Solid Cylinder FAQs
What is a solid cylinder?
A solid cylinder is a three-dimensional geometric shape with two parallel circular bases of the same size and shape connected by a curved surface, giving it a uniform distribution of mass.
What is the moment of inertia of a solid cylinder?
The moment of inertia of a solid cylinder depends on its mass, radius, and axis of rotation, and is calculated using the formula (1/2) * mass * radius^2.
What is the formula for moment of inertia of a cylinder?
The formula for the moment of inertia of a cylinder depends on whether it's solid or hollow, and whether you're calculating it about its central axis or a different axis.
What is the moment of inertia of a solid cylinder about the end?
The moment of inertia of a solid cylinder about its end is (1/4) * mass * radius^2.
What is the moment of inertia of a solid cylinder about its geometrical axis?
The moment of inertia of a solid cylinder about its geometrical axis (central axis) is (1/2) * mass * radius^2.
