Table of Contents
Moment of Inertia of Flywheel: Flywheels seem to be circular disc-shaped objects that are used to store energy in machines. The flywheel has been made up of a large circular disc/massive wheel with a strong axle protruding on either side. The axle would be supported by two fixed supports and is mounted on ball bearings. Just on the axle, there is a small peg. The weight-hanger is carried by one end of a cord that is loosely looped around the peg.
The formula that is used to calculate the moment of inertia of a flywheel is:
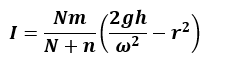
In which, I = moment of inertia of the flywheel. Here, the symbols denote;
m = rings’ mass.
N = flywheel rotation.
n = number of windings of the string.
h = height of the weight assembly.
g = acceleration due to gravity.
r = radius of the axle.
Similarly, we can also use the following expression;
mgh = ½ mv2 + ½ Iω2 + n1E
Determining the Moment of Inertia of Flywheel
A few important factors must be considered when determining the moment of inertia of a flywheel. Initially, we must assemble a flywheel, as well as equipment such as a weight hanger, slotted weights, a metre scale, and a stopwatch.
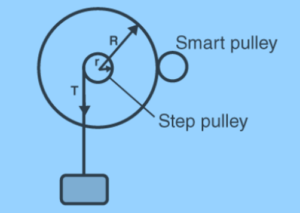
Afterwards, we make some assumptions. We’ll use mass (m) for both the weight hanger and the hanging ring. The maximum height will be (h). Just consider a situation in which the mass will descend to a new height. There’ll be some potential energy loss, which we can express as follows in the equation:
Ploss = mgh
In the meantime, when the flywheel and axle rotate, there is a gain in kinetic energy. We say it this way:
Kflywheel = (½) Iω2
I = moment of inertia
ω = angular velocity
Correspondingly, the kinetic energy of descending weight assembly is written as;
Kweight = (½) Iv2
Here, v = veocity
We must also consider the effort expended in overcoming the friction. It can be determined by;
Wfriction = nWf
In this particular instance,
n = number of windings of the string
Wf = work done in overcoming frictional torque
When we state the law of conservation of energy then we obtain;
Ploss = Kflywheel + Kweight + Wfriction
Now, We’ll substitute the values and the equation will now become;
mgh = (½)Iω2 + (½) mv2 + nWf
Shifting on to the next phase, we examine the kinetic energy of the flywheel assembly as it rotates (N) times against the frictional torque. We obtain;
NWf = (½ ) Iω2 and Wf = (1 / 2N) Iω2
Moreover, we establish a relationship between the weight assembly’s velocity (v) and the axle’s radius (r). The equation is as follows:
v = ωr
Now, we need to substitute the values for Wf and v.
mgh = (½) Iω2 + (½ )mr2ω2 + (n / N) x ½ Iω2
When we solve the equation for finding the moment of inertia of flywheel, we obtain;
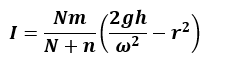
FAQs
What is meant by MOI of the flywheel?
The moment of inertia of a body has been defined as the object's resistance to rotational changes. The flywheel flexibly rotates about a horizontal axis. A calliper could be used to measure the radius of the flywheel's axile.
What is the main focus of the flywheel experiment?
The moment of inertia of a flywheel has been investigated by varying the flywheel's point of mass. The experiment has been carried out by recording the time taken by a fixed load until the point at which the load escapes from the flywheel, as well as the number of rotations performed afterwards, which is independent of the load.



