Table of Contents
You might have heard about Moment of Inertia. But what is the Moment of Inertia of Rectangle? How to you calculate the Moment of Inertia of a rectangular section? If you are wondering where to get answers to these questions, you are on the right page. This article answers all your questions related to moment of inertia of rectangle and provides the readers with all the required information.
Join Our Online Courses for JEE: JEE Class 11 Online Course | JEE Class 12 Online Course | JEE Dropper Online Course
Moment of Inertia of Rectangle An Axis Passing Through Its Centroid
In the particular instance where the axis passes through the centroid, the moment of inertia of the rectangle is given as follows:
I = bh3 / 12
The rectangle width (a dimension parallel to the axis) has been denoted by b, and the height is denoted by h (dimension perpendicular to the axis).
Moment of Inertia of Rectangle An Axis Passing Through Its Base
The moment of inertia of a rectangle has been expressed as follows when an axis passes through the base:
I = bh3 / 3
It is seamlessly determined by applying the Parallel Axis Theorem because the rectangle centroid is located at a distance equal to h/2 from the base.
Parallel Axis Theorem
The parallel axis theorem could be used to calculate the area moment of inertia of any shape present in any parallel axis. If we recognize the moment of inertia of the non-centroidal axis with respect to a centroidal axis parallel to the first, we can find it here. Typically, the equation is written as;
I = Ix + Ad2
- Ix = moment of inertia in arbitrary axis
- A = area of the shape
- D is said to be the perpendicular distance between the x and x’ axes.
A Centroidal Axis Perpendicular to Its Base
By alternating the dimensions b and h from the first equation given above, we can determine the moment of inertia of a rectangle by taking the centroidal axis perpendicular to its base. We’ll get the following equation as a result:
Iy = hb3/ 12
How to Calculate Moment of Inertia of Rectangle Section
We’ll start with one rectangular section ABCD, as shown in the figure below. We would then assume that one of the lines will pass through the rectangular section’s base. We’ll use this line as the line CD. Now we’ll calculate the area moment of inertia for the rectangular section centered on this line CD.
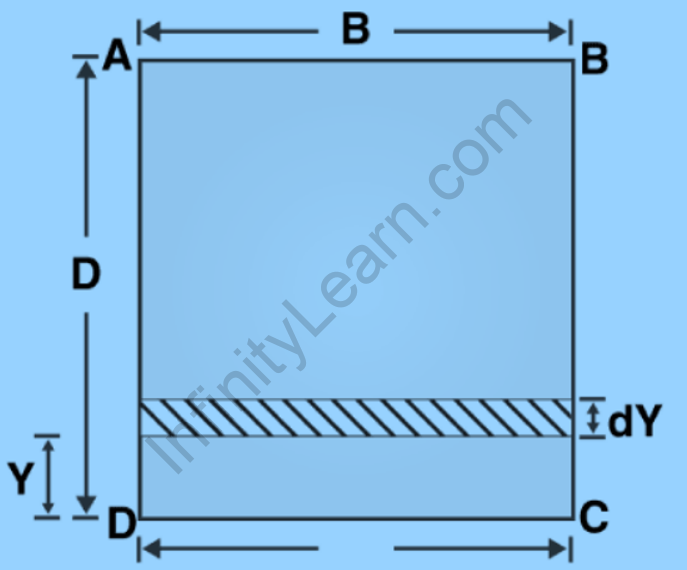B is said to be the width of the ABCD rectangular section- D is said to be the depth of the ABCD rectangular section
- ICD is said to be the moment of inertia of the rectangular section about the CD line
- The next step is to calculate or express the moment of inertia of the rectangular plate about the line CD. In this case, we’ll use one rectangular elementary strip with a thickness dY that’s Y distance from the line CD.
- dA = dY.B is the area of the rectangular elementary strip.
- Now, the moment of inertia about the line CD = dA.Y2 = B Y2 dY
B is said to be the width of the ABCD rectangular sectionFollowing the determination of the moment of inertia of the rectangular section about the line CD, we will proceed to determine the moment of inertia of the entire area of the rectangular cross-section centered on the line CD. We would then integrate the above equation from limit 0 to limit D.
The moment of inertia of the whole rectangular section about the line CD has been typically given as;
ICD = O ∫D B Y2 dY
ICD = B O ∫D Y2 dY
ICD = B [y3 / 3]OD
ICD = BD3 / 3
Thus, the moment of inertia of the rectangular section about the line CD
ICD = BD3 / 3
| Related Post | |
| Moment of Inertia of a Ring | Moment Of Inertia of A Circle |
| How to Calculate Moment of Inertia | Moment of Inertia of Semicircle |
| Moment Of Inertia Of a Sphere | Moment of Inertia of a Cone |
FAQs on Moment of Inertia of Rectangle
What is the formula for the moment of inertia of a rectangular plate?
The formula for the moment of inertia of a rectangular plate is (1/12) * mass * (length^2 + width^2).
How do you calculate the moment of inertia?
Moments of inertia could be calculated by adding or integrating the sum of all 'pieces of mass' that make up an object, multiplied by the square of the distance of each 'piece of mass' from the axis.
What is the moment of inertia of a rectangle?
In the case where the axis passes through the centroid, the moment of inertia of a rectangle is given as I = bh3 / 12.
What is the formula for the moment of inertia of a shape?
The formula for the moment of inertia of a shape depends on the specific shape and its axis of rotation, so there isn't a single universal formula for all shapes.
What is the formula for moment of inertia of all shapes?
There isn't a single formula for the moment of inertia of all shapes; it varies with the shape's geometry.
What is the moment of inertia of a triangle?
The moment of inertia of a triangle depends on its dimensions and axis of rotation, and it's calculated differently than that of a rectangle.
What is the centroid of a rectangle?
The centroid of a rectangle is the point of intersection of its diagonals, which is equidistant from all four corners.
