Spherometer: Determining Radius of Curvature of Spherical surface

What is a spherometer? How do you use it to determine the radius of curvature of a given spherical surface?

Aim

To determine the radius of curvature of a given spherical surface by a spherometer.

Apparatus
Spherometer, convex surface (it may be an unpolished convex mirror), a big size plane glass slab, or plane mirror.

Diagram

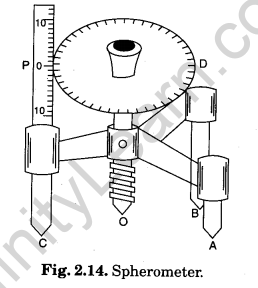
Theory
It works on the principle of micrometer screw. It is used to measure either very small thickness or the radius of curvature of a spherical surface which is why it is called a spherometer.

Procedure

1. Raise the central screw of the spherometer and press the spherometer gently on the practical notebook so as to get pricks off the three legs. Mark these pricks as A, B, and C.
2. Measure the distance between the pricks (points) by joining the points to form a triangle ABC.
3. Note these distances (AB, BC, AC) in the notebook and take their mean.
4. Find the value of one vertical {pitch) scale division.
5. Determine the pitch and the least count of the spherometer [Art. 2.13(c)] and record it step-wise.
6. Raise the screw sufficiently upwards.
7. Place the spherometer on the convex surface so that its three legs rest on it.
8. Gently, turn the screw downwards till the screw tip just touches the convex surface. (The tip of the screw will just touch its image on the convex glass surface).
9. Note the reading of the circular (disc) scale which is in line with the vertical (pitch) scale. Let it be a (It will act as a reference).
10. Remove the spherometer from over the convex surface and place it over a large size plane glass slab.
11. Turn the screw downwards and count the number of complete rotations (n₁) made by the disc (one rotation becomes complete when the reference reading crosses past the pitch scale).
12. Continue till the tip of the screw just touches the plane surface of the glass slab.
13. Note the reading of the circular scale which is finally in line with the vertical (pitch) scale. Let it be b.
14. Find the number of circular (disc) scale divisions in the last incomplete rotation.
15. Repeat steps 6 to 14, three times. Record the observation in tabular form.

Observations

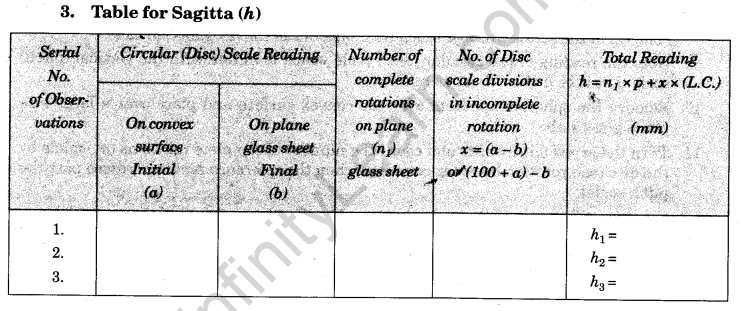
Calculations
1. Find the value of h in each observation and record it in column 5.
2. Find the mean of the value of h recorded in column 5

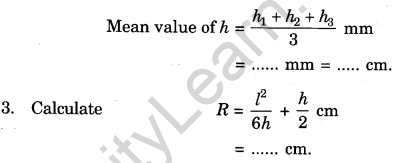
Result
The radius of curvature of the given convex surface is cm.

Precautions

1. The screw should move freely without friction.
2. The screw should be moved in the same direction to avoid the back-lash error of the screw.
3. Excess rotation should be avoided.

Sources of error

1. The screw may have friction.
2. The spherometer may have a back-lash error.
3. Circular (disc) scale divisions may not be of equal size.

Viva Voce

Question.1. Describe the principle of a spherometer.
Answer. It works on the principle of a micrometer screw.

Question.2. Why is a spherometer so called?
Answer. It measures the radius of curvature of spherical surfaces, hence it is called a spherometer.

Question.3. Give the formula for the determination of the radius of curvature by a spherometer.
Answer.

Question.4. What are the values of P and R? for a plane surface?
Answer. For a plane surface,
P = 0 and R = infinite.

Question.5. What is meant by the pitch of the spherometer?
Answer. The pitch is the distance between two consecutive threads of the screw taken parallel to the axis of rotation or the distance moved by the screw in one complete rotation of the circular scale.

Question.6. How can the accuracy of a spherometer be increased?
Answer. The smaller is the least count, the more is the accuracy of an instrument and vice versa. The accuracy of the spherometer can be increased by decreasing the pitch or by increasing the number of divisions of the circular scale.

Question.7. The least count of screw gauge and spherometer is the same. Which will you prefer to measure the radius of curvature of the lens or mirror?
Answer. The spherometer.

Question.8. Write Len’s maker formula.
Answer. The focal length of a lens

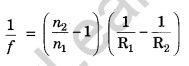
Question.9. Can you measure the focal length of a lens?
Answer. Yes, by measuring R₁ and R₂ by spherometer n₁ = 1 and n₂ is known refractive index of the material of the lens.

Question.10. Why is the good spherometer made of gunmetal?
Answer. To minimize wear and tear.