Table of Contents
The CBSE Class 10 Maths exam is an important milestone for students, testing their understanding of mathematical concepts and problem-solving skills. After the exam, students eagerly await the release of the answer key to check their answers and assess their performance. In this blog, we will provide an analysis of the CBSE Class 10 Maths answer key 2024 for sets 1, 2, and 3.
New: CBSE Class 10th Result Date 2024 | CBSE Class 10 Passing Criteria & Study Hacks
CBSE Class 10 Maths Paper 2024
The CBSE Class 10 Maths Paper 2024 will be held on March 11, 2024, from 10:30 am to 1:30 pm.
| Particulars | Details |
| CBSE 10th Maths exam date | 11 Mar 2024 |
| CBSE 10th Maths exam timing | 10:30 am to 1:30 pm |
| CBSE 10th Maths answer key (Unofficial) | 11 Mar 2024 |
| CBSE 10th Maths answer key (Official) | April 2024 (tentative) |
| CBSE 10th Maths Total marks | 100 |
| CBSE 10th Maths Marking Scheme | Objective Type Questions |
| Short Answer Type | |
| Long Answer Type | |
| Negative marking | No |
CBSE Class 10 Maths Answer Key
The CBSE Class 10 Maths answer key is a document that contains the correct answers to all the questions asked in the Maths exam. It is released by various coaching institutes and educational websites shortly after the exam to help students evaluate their performance and calculate their expected scores.
CBSE Class 10 Maths Answer Key & Paper Analysis: The CBSE Class 10 Maths answer key 2024 for sets 1, 2, and 3 provides a detailed analysis of the exam paper. It includes the following key points:
- Difficulty Level: The answer key indicates the overall difficulty level of the exam. It helps students understand the complexity of the questions and their preparedness.
- Topic-wise Analysis: The answer key breaks down the questions according to the topics covered in the syllabus. This analysis helps students identify their strengths and weaknesses in each subject.
- Expected Cutoff: Based on the analysis of the answer key, experts predict the expected cutoff marks for the exam. This information is crucial for students to gauge their chances of qualifying for the next stage of the selection process.
CBSE Class 10 Maths Answer Key for Set 1, 2 & 3 – Paper Analysis
The CBSE Class 10 Maths paper 2024 contained a total of six sections. Each section consisted of different question types. The difficulty level for each section depended on the nature of the question. The table below shows the section-wise analysis of the CBSE Class 10 Maths question paper 2024.
| Units | Unit Name | Marks |
| I | Number System | 06 |
| II | Algebra | 20 |
| III | Coordinate Geometry | 06 |
| IV | Geometry | 15 |
| V | Trigonometry | 12 |
| VI | Mensuration | 10 |
| VII | Statistics & Probability | 11 |
| Total | 80 |
CBSE Class 10 Maths Paper 2024 with Answers Keys for All Sets
SECTION A
This section comprises Multiple Choice Questions (MCQs) of 1 mark each. 20×1=20
1. The next (4th) term of the A.P. √18, √50, √98, is:
(A) √128
(C) √162
(B) √140
(D) √200
2. If 3 = 2 sin A, 3 = 2 cos A, then the value of x2 + y2 is:
(A) 36
(B) 9
(C) 6
(D) 18
3. If 4 sec 0-5 = 0, then the value of cot 0 is:
(A) 3/4
(C) 5/3
(B) 4 /5
(D) 4/ 3
4. Which out of the following type of straight lines will be represented by the system of equations 3x + 4y = 5 and 6x + 8y = 7 ?
(A) Parallel
(B) Intersecting
(C) Coincident
(D) Perpendicular to each other
5. The ratio of the sum and product of the roots of the quadratic equation 5×2-6x+21 = 0 is :
(A) 5:21
(C) 21:5
(B) 2:7
(D) 7:2
6. For the data 2, 9, x + 6, 2x + 3, 5, 10, 5; if the mean is 7, then the value of x is:
(A) 9
(B) 6
(C) 5
(D) 3
7. One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 7 is:
(A) 1/7
(C) 1 /5
(B) 1/ 8
(D) 7/ 40
8. The perimeter of the sector of a circle of radius 21 cm which subtends an angle of 60° at the centre of circle, is:
(A) 22 cm
(B) 43 cm
(C) 64 cm
(D) 462 cm
9. The length of an arc of a circle with radius 12 cm is 10 cm. The angle subtended by the arc at the centre of the circle, is :
(A) 120°
(B) 6°
(C) 75°
(D) 150°
10. The greatest number which divides 281 and 1249, leaving remainder 5 and 7 respectively, is :
(A) 23
(B) 276
(C) 138
(D) 69
11. The number of terms in the A.P. 3, 6, 9, 12, …, 111 is:
(A) 36
(C) 37
(B) 40
(D) 30
12. A chord of a circle of radius 10 cm subtends a right angle at its centre. The length of the chord (in cm) is

(A) 5√2
(B) 10/2
(C) 5 √2
(D) 5
13. The LCM of three numbers 28, 44, 132 is:
(A) 258
(B) 231
(C) 462
(D) 924
14. If the product of two co-prime numbers is 553, then their HCF is :
(A) 1
(C) 7
(B) 553
(D) 79
15. If a and ẞ are the zeroes of the polynomial p(x) = kx² – 30x + 45k and α + β = αβ, then the value of k is :
(A) -2/3
(C) 3/2
(B) -3/2
(D) 2/3
16. In the given figure, RJ and RL are two tangents to the circle. If RJL = 42°, then the measure of ✓ JOL is:

(A) 42°
(B) 84°
(C) 96°
(D) 138°
17. In the given figure, in A ABC, DE || BC. If AD = 2.4 cm, DB = 4 cm and AE = 2 cm, then the length of AC is :
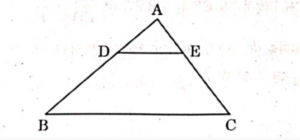
(A)10/3 cm
(B) 3/10cm
(C) 16/3 cm
(D) 1.2 cm
18. If a vertical pole of length 7.5 m casts a shadow 5 m long on the ground and at the same time, a tower casts a shadow 24 m long, then the height of the tower is:
(A) 20 m
(B) 40 m
(C) 60 m
(D) 36 m
CBSE Class 10 Maths Answer Key Set 1 Download PDF
CBSE Class 10 Maths Paper 2024 with Answers Keys Set 1 with Solution
Section A
This section comprises multiple choice questions (MCQ) of 1 mark each.
1. The number of polynomials having zeroes-3 and 5 is:
(a) only one
(b) infinite
(c) exactly two
(d) at most two
Correct answer: (b) infinite
2. The pair of equations ax + 2y = 9 and 3x+ by = 18 represent parallel lines, where a, b are integers, if:
(a) a= b
(b) 3a=2b
(c) 2a=3b
(d) ab=6
Answer: (d) ab=6
3. The common difference of the A.P. whose nth term is given by a 3n+7,
(a) 7
(b) 3
(c) 3n
(d) 1
Answer:(b)3
4. In the given figure, DE || BC. The value of x is

(a) 6 (b) 12.5
(c) 8 (d) 10
Answer:(d) 10
5. A quadratic equation whose roots are (9 + sqrt(3)) and (2 – sqrt(3)) * i * 2
(a) x ² – 4x + 1 = 0
(b)x ² + 4x + 1 = 0
(c) 4x ² – 3 = 0
(d)x ² – 1 = 0
Answer: (a) x ² – 4x + 1 = 0

Answer: (a) -17/13
7. The distance between two points P(-11/3,5) and Q(-2/3,5) is
(a) 6 units (b) 4 units
(c) 2 units (d) 3 units
Answer:(d) 3 units
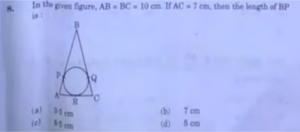
Answer: (c) 6.5 cm
9. Water in a river which is 3 m deep and 40 m wide is flowing at the rate of 2 km/h. How much water will fall into the sea in 2 minutes?
(a) 800 m³
(b) 4000 m³
(c) 8000 m³
(d) 2000 m³
Answer: (c) 8000 m³
10. If the mean and the median of a data are 12 and 15 respectively, then its mode is:
(a) 13.5
(b) 21
(c) 6
(d) 14
Answer; (b) 21
11. In the given figure, AB is a tangent to the circle centered at O. If OA 6 cm and OAB 30″, then the radius of the circle is:

13.

Correct answer (b)
14. The 11th term from the end of the A.P.: 10, 7, 4, 62 is:
(a) 25
(b) 16
(c) -32
(d) 0
Correct answer (c)
15. Two coins are tossed together. The probability of getting at least one tail is:
(a)1/4
(b)1/2
(C)3/4
(d) 1
Correct answer (c)
16. In the given figure, AC and AB are tangents to a circle centered at O. If 2 COD 120, then BAO is equal to:
Correct answer (a)
17. Which of the following numbers cannot be the probability of happening of an event?
(a) 0
(b) 7/0.01
(c) 0.07
(d) 0.07 /3
Correct answer (b)
18. If every term of the statistical data consisting of n terms is decreased by 2, then the mean of the data:
(a) decreases by 2
(b) remains unchanged
(C) decreases by 2n
(d) decreases by 1
Correct answer (a)
19 Find the sum of first 30 terms of AP: -30, 24, -18,/..
Solution: a= -30, d= 6
= 15 [-60 + 29 (6)]
= 15 [-60+174]
= 15 [114]
= 1710
OR
If an AP is Sn = n(4n+1), then find the AP
Solution: S1 = T1 = 5
S2= T1 + T2= 18
S2-S1 = T2= 13
AP= 5, 13, 21, 29, …
21. A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
Solution: r1 = 10.5 cm (sphere) and r2 (cone)= 3.5 cm, h2= 3cm
4/3πr³ = n x 1/3πr2² h
4r³ = nr2² h
4 x (105/10)³= n x 35/10 x 35/10 x 3
21 x 6= n
Number of cones formed= 126
22. (a) Find the value of m for which the quadratic equation
(m-1) x² + 2(m-1)x + 1 = 0
Solution: D= 0
4 (m-1)² – 4(m-1) = 0
4 (m-1) [m-1-1]= 0
(m-1) (m-2)= 0
m= 2
(b) Solve the following quadratic equation for x: √3x² + 10x + 7√3= 0
Solution: √3x² + 3x + 7x + 7√3= 0
√3x (x+ √3) + 7 (x + √3)= 0
(x+ √3) [√3x + 7]= 0
x= √3 || x= -7/√3
23. Find the mode of the following frequency distribution:
Class 10-20 20-30 30-40 40-50 50-60
Frequency 15 10 12 17 4
Solution: l= 40, f1= 17, f2= 4, fo= 12
Mode= l + f1-fo / 2f1 – fo- f2
= 40 + 17-12 / 34-12-4 x 10
= 40 + 5/18 x 10
= 40 + 25/9
= 40 + 2.78
= 42.78
Q.5: The product of Rehan’s age (in years) 5 years ago and his age 7 years from now, is one more than twice his present age. Find his present age.
Solution:
Past Age Present Age Future Age
x-5 x x+7
(x-5) (x+7) = 2x + 1
x² + 2x -35 = 2x+1
x² – 36 = 0
x² = 36
x= +_ 6
Present Age- 6 years
Q.6 Two concentric circles are of radii 4 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:

Section B
Q.7: For what value of x, is the median of the following frequency distribution 34:5?
Class Frequency
0-10 3
10-20 5
20-30 11
30-40 10
40-50 x
50-60 3
60-70 2
Solution:

Q.8: Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Construct tangents to the circle from these two points P and Q.
Solution:

Q.9: (a) The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, then find the height of the building.
Solution:
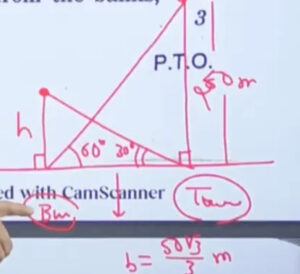
tan 60° = 50/b
b= 50/ tan 60°
b = 50/ √3
b= 50√3 / 3
tan 30° = h/(50√3/3)
h= 50√3/3 x 1/√3
= 50/3 m= 16.67 metres
OR
Q.9:(b) From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, then find the width of the river.
Solution:
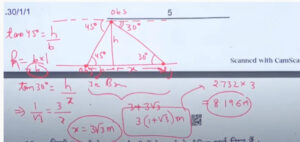
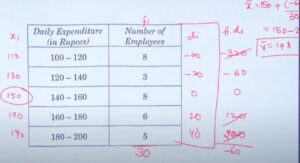
Q.10: Following is the daily expenditure on lunch by 30 employees of a company, Find the mean daily expenditure of the employees.
Solution:
Q.11: From a solid cylinder of the height of 30 cm and radius of 7 cm, a conical cavity of height of 24 cm and same radius is hollowed out. Find the total surface area of the remaining solid.
Solution: H= 30 cm
R= 7 cm
Total Surface Area of Cylinder = Curved Surface Area of Cylinder + Curved Surface Area of Cone + πr²
TSA = 2 πrh + πrl + πr²
= πr (2h+ l+ r)
= 22/7 x 7 (60+25 + 7)
= 22 x 92
TSA= 2024 cm
Q.12: In figure 1, a traingle ABC with angle B = 90 degrees is shown. Taking AB as diameter, a circle has been drawn intersecting AC at point P. Prove that the tangent drawn at point P bisects BC.

Case Study:1
Q.13: In Mathematics, relations can be expressed in various ways. The matchstick patterns are based on linear relations. Different strategies can be used to calculate the number of matchsticks used in different figures.

One such pattern is shown below. Observe the pattern and answer the following questions using Arithmetic Progression::
(a) Write the AP for the number of triangles used in the figures. Also, write the nth term of this AP. Which figure has 61 matchsticks?
Solution- AP = 4, 6, 8, 10
a= 4, d= 2
Tn = 4 + 2(n-1)
Tn= = 4 + 2n – 2
Tn= 2n +2
(b) Which figures has 61 matchstickes?
Solution: 12, 19, 26, …
Tn = 61
a + (n-1) d= 61
12 + 7(n-1) = 61
7(n-1) = 49
n-1 = 7
n= 8
8th figure has 61 matchsticks
Q.14 Gadisagar lake is located in the jaisalmer district of Rajasthan. It was built by king of jaisalmer ad rebuilt by Gadsi Singh in 14th Century. The lake has many chattris. One of them is shown below:

Observe the picture. From a point A h m above from water level, the angle of elevation of top of chattari (point B) is 45 degrees and angle of depression of its reflection in water(Point C) is 60 degrees. If the height of chhattri above the water level is 10m, then
a) Draw a well-labelled figure based on the above information;
b) Find the height of the point A above the water level.
(Use √3 = 1.73)
Solution:







