Table of Contents
Important Questions for Class 10 Maths Chapter 11 Constructions
Constructions Class 10 Important Questions Short Answer-I (2 Marks)
Question 1.
Draw a line segment of length 6 cm. Using compasses and ruler, find a point P on it which divides it in the ratio 3 : 4. (2011D)
Solution:
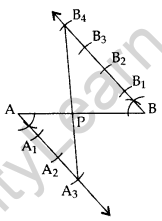
Hence, PA : PB = 3 : 4
Question 2.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB such that \(\frac{\mathbf{A} \mathbf{P}}{\mathbf{A B}}=\frac{3}{5}\). (2011OD)
Solution:
AB = 7 cm, AB = \(\frac{\mathbf{A} \mathbf{P}}{\mathbf{A B}}=\frac{3}{5}\) … [Given
∴ AP : PB = 3 : 2
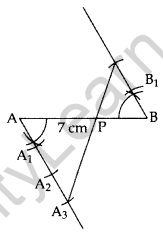
Hence, AP : AB = 3 : 5 or \(\frac{\mathbf{A} \mathbf{P}}{\mathbf{A B}}=\frac{3}{5}\)
Constructions Class 10 Important Questions Short Answer-II (3 Marks)
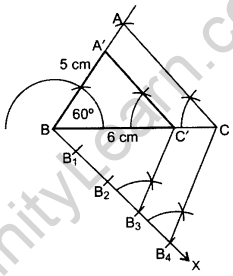
Question 3.
Draw a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Then construct a triangle whose sides are \(\frac{5}{7}\) times the corresponding sides of ∆ABC. (2011D)
Solution:
In ∆ABC
AB = 5 cm
BC = 6 cm
∠ABC = 60°
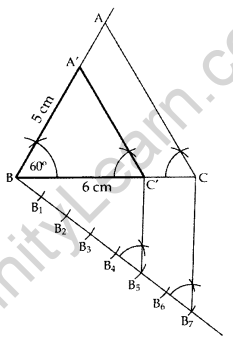
Hence, ∆A’BC’ is the required ∆.
Question 4.
Construct a triangle with sides 5 cm, 5.5 cm and 6.5 cm. Now construct another triangle, whose sides are \(\frac{3}{5}\) times the corresponding sides of the given triangle. (20140D)
Solution:
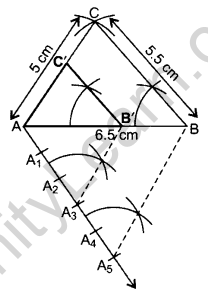
∴ ∆AB’C’ is the required ∆.
Question 5.
Construct a right triangle in which the sides, (other than the hypotenuse) are of length 6 cm and 8 cm. Then construct another triangle, whose sides are \(\frac{3}{5}\) times the corresponding sides of the given triangle. (2012D)
Solution:
Here AB = 8 cm, BC = 6 cm and
Ratio = \(\frac{3}{5}\) of corresponding sides
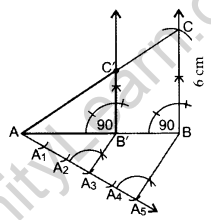
∴ ∆AB’C’ is the required triangle.
Question 6.
Draw a triangle PQR such that PQ = 5 cm, ∠P = 120° and PR = 6 cm. Construct another triangle whose sides are \(\frac{3}{4}\) times the corresponding sides of ∆PQR. (2011D)
Solution:
In ∆PQR,
PQ = 5 cm, PR = 6 cm, ∠P = 120°
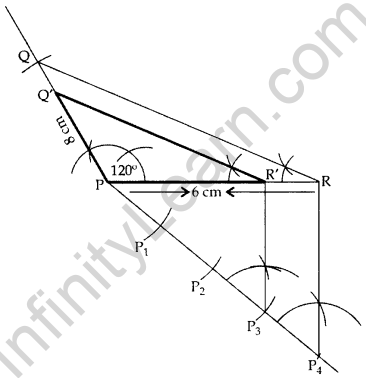
∴ ∆POʻR’ is the required ∆.
Question 7.
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠C = 60°. Then construct another triangle, whose sides are \(\frac{3}{5}\) times the corresponding sides of ∆ABC. (2012OD)
Solution:
Here, BC = 7 cm, ∠B = 45°, ∠C = 60° and ratio is \(\frac{3}{5}\) times of corresponding sides
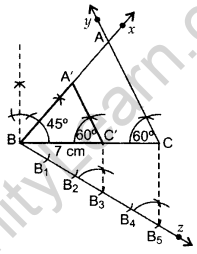
∴ ∆A’BC’ is the required triangle.
Question 8.
Construct a triangle with sides 5 cm, 4 cm and 6 cm. Then construct another triangle whose sides are \(\frac{2}{3}\) times the corresponding sides of first triangle. (2013D)
Solution:
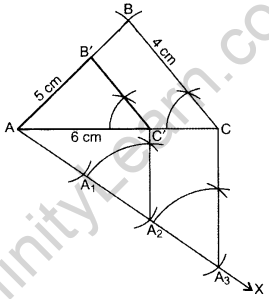
Steps of Construction:
- Draw ∆ABC with AC = 6 cm, AB = 5 cm, BC = 4 cm.
- Draw ray AX making an acute angle with AÇ.
- Locate 3 equal points A1, A2, A3 on AX.
- Join CA3.
- Join A2C’ || CA3.
- From point C’ draw B’C’ || BC.
∴ ∆AB’C’ is the required triangle.
Question 9.
Draw a pair of tangents to a circle of radius 3 cm, which are inclined to each other at an angle of 60°. (2011OD)
Solution:
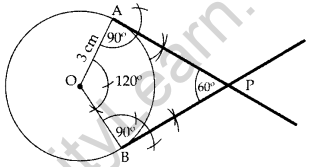
∴ PA & PB are the required tangents.
Question 10.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm. (2013D)
Solution:
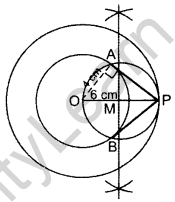
Steps of Construction:
Draw two circles with radius OA = 4 cm and OP = 6 cm with O as centre. Draw ⊥ bisector of OP at M. Taking M as centre and OM as radius draw another circle intersecting the smaller circle at A and B and touching the bigger circle at P. Join PA and PB. PA and PB are the required tangents.
Verification:
In rt. ∆OAP,
OA2 + AP2 = OP2 … [Pythagoras’ theorem
(4)2 + (AP)2 = (6)2
AP2 = 36 – 16 = 20
AP = + \(\sqrt{20}=\sqrt{4 \times 5}\)
= \(2 \sqrt{5}\) = 2(2.236) = 4.472 = 4.5 cm
By measurement, ∴ PA = PB = 4.5 cm
Question 11.
Draw a pair of tangents to a circle of radius 4.5 cm, which are inclined to each other at an angle of 45°. (2013OD)
Solution:
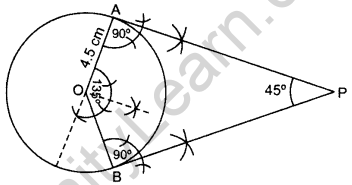
Draw ∠AOB = 135°, ∠OAP = 90°, ∠OBP = 90°
∴ PA and PB are the required tangents.
Question 12.
Draw two tangents to a circle of radius 3.5 cm, from a point P at a distance of 6.2 cm from its cehtre. (2013OD)
Solution:
OP = OC + CP = 3.5 + 2.7 = 6.2 cm
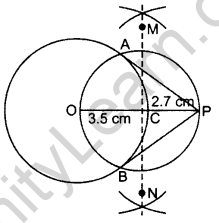
Hence AP & PB are the required tangents.
Question 13.
Draw a right triangle ABC in which AB = 6 cm, BC = 8 cm and ∠B = 90°. Draw BD perpendicular from B on AC and draw a circle passing through the points B, C and D. Construct tangents from A to this circle. (2014D, 2015OD)
Solution:
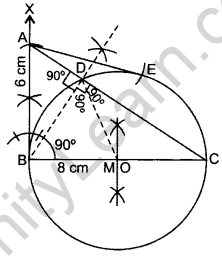
Steps of Construction:
- Draw BC = 8 cm.
- From B draw an angle of 90°.
- Draw an arc BA = 6 cm cutting the angle at A.
- Join AC. ∴ ∆ABC is the required ∆.
- Draw ⊥ bisector of BC cutting BC at M.
- Take Mas centre and BM as radius, draw a circle.
- Take A as centre and AB as radius draw an arc cutting the circle at E. Join AE.
AB and AE are the required tangents.
Justification: ∠ABC = 90° …[Given
Since, OB is a radius of the circle.
∴ AB is a tangent to the circle.
Also, AE is a tangent to the circle.
Question 14.
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle. (2014OD)
Solution:
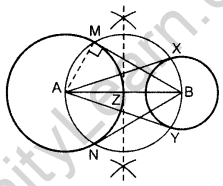
Draw two circles on A and B as asked.
Z is the mid-point of AB.
From Z, draw a circle taking ZA = ZB as radius,
so that the circle intersects the bigger circle at M and N and smaller circle at X and Y.
Join AX and AY, BM and BN.
BM, BN are the reqd. tangents from external point B.
AX, AY are the reqd. tangents from external point A.
Justification:
∠AMB = 90° …[Angle in a semi-circle
Since, AM is a radius of the given circle.
∴ BM is a tangent to the circle
Similarly, BN, AX and AY are also tangents.
Constructions Class 10 Important Questions Long Answer (4 Marks).
Question 15.
Draw a triangle ABC with side BC = 7 cm, ∠B = 45° and ∆A = 105°. Then construct a triangle whose sides are \(\frac{3}{5}\)times the corresponding sides of ∆ABC. (2011D)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° … [angle sum property of a ∆
105° + 45° + C = 180°
∠C = 180° – 105° – 45o = 30°
BC = 7 cm
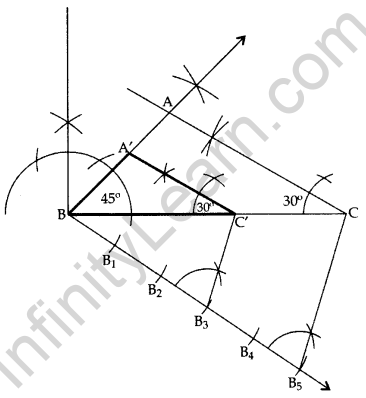
∴ ∆A’BC’ is the required ∆.
Question 16.
Draw a triangle ABC with side BC = 6 cm, ∠C = 30° and ∠A = 105°. Then construct another triangle whose sides are \(\frac{2}{3}\) times the corresponding sides of ∆ABC. (2012D)
Solution:
Here, BC = 6 cm, ∠A = 105o and ∠C = 30°
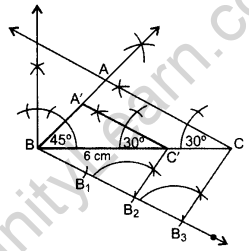
In ∆ABC,
∠A + ∠B + ∠C = 180° …[Angle-sum-property of a ∆
105° + ∠B + 30o = 180°
∠B = 180° – 105° – 30o = 45°
∴ ∆A’BC’ is the required ∆.
Question 17.
Draw a triangle with sides 5 cm, 6 cm and 7 cm. Then construct another triangle whose sides are \(\frac{2}{3}\) times the corresponding sides of the first triangle. (2012OD)
Solution:
Here, AB = 5 cm, BC = 7 cm, AC = 6 cm and ratio is \(\frac{2}{3}\) times of corresponding sides.
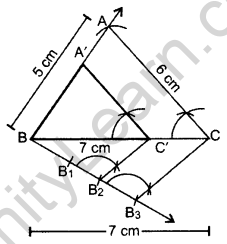
∴ ∆A’BC’ is the required triangle.
Question 18.
Construct an isosceles triangle whose base is 6 cm and altitude 4 cm. Then construct another triangle whose sides are \(\frac{3}{4}\) times the corresponding sides of the isosceles triangle. (2015D)
Solution:
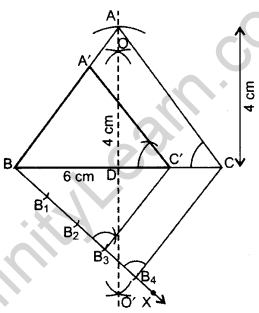
∴ ∆A’BC’ is the required triangle.
Question 19.
Draw a line segment AB of length 7 cm. Taking A as centre, draw a circle of radius 3 cm and taking B as centre, draw another circle of radius 2 cm. Construct tangents to each circle from the centre of the other circle. (2015D)
Solution:
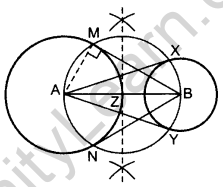
Draw two circles on A and B as asked.
Z is the mid-point of AB.
From Z, draw a circle taking ZA = ZB as radius,
so that the circle intersects the bigger circle at M and N and smaller circle at X and Y.
Join AX and AY, BM and BN.
BM, BN are the required tangents from external point B.
AX, AY are the required tangents from external point A.
Justification:
∠AMB = 90° …[Angle in a semi-circle
Since, AM is a radius of the given circle.
∴BM is a tangent to the circle
Similarly, BN, AX and AY are also tangents.
Question 20.
Construct a ∆ABC in which AB = 6 cm, ∠A = 30° and ∆B = 60°. Construct another ∆AB’C’ similar to ∆ABC with base AB’ = 8 cm. (2015OD)
Solution:
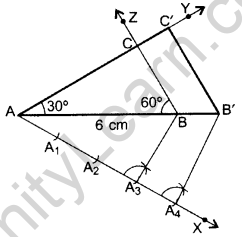
Steps of construction:
- Draw a ∆ABC with side AB = 6 cm, ∠A = 30° and ∠B = 60°.
- Draw a ray AX making an acute angle with AB on the opposite side of point C.
- Locate points A1, A2, A3 and A4 on AX.
- Join A3B. Draw a line through A4 parallel to A3B intersecting extended AB at B’.
- Draw a line parallel to BC intersecting ray AY at C’.
Hence, ∆AB’C’ is the required triangle.
Question 21.
Construct a triangle ABC in which AB = 5 cm, BC = 6 cm and ∠ABC = 60°. Now construct another triangle whose sides are \(\frac{5}{7}\) times the corresponding sides of ∆ABC. (2015OD)
Solution:
In ∆ABC, AB = 5 cm; BC = 6 cm; ∠ABC = 60°
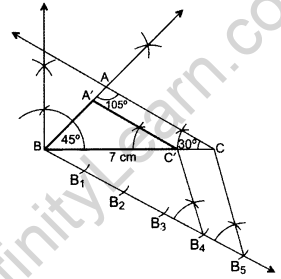
∴ ∆A’BC’ is the required ∆.
Question 22.
Construct a triangle ABC in which BC = 6 cm, AB = 5 cm and ∠ABC = 60°. Then construct another triangle whose sides are \(\frac{3}{4}\) times the corresponding sides of ∆ABC. (2016D)
Solution:
Steps of Construction:
- Draw ∆ABC with the given data.
- Draw a ray BX downwards making an acute angle with BC.
- Locate 4 points B1, B2, B3, B4, on BX, such that BB1 = B1B2 = B2B3 = B3B4.
- Join CB4.
- From B3 draw a line C’B3 || CB4 intersecting BC at C’.
- From C’ draw A’C’ || AC intersecting AB at B’.
Then ∆AB’C’ in the required triangle.
Justification:

Question 23.
Draw a triangle ABC with BC = 7 cm, ∠B = 45° and ∠A = 105°. Then construct a triangle whose sides are \(\frac{4}{5}\) times the corresponding sides of ∆ABC. (2016D)
Solution:
In ∆ABC, ∠A + ∠B + ∠C = 180° ..[Angle-sum-property of a ∆
105° + 45° + ∠C = 180°
∠C = 180° – 105° – 45o = 30°
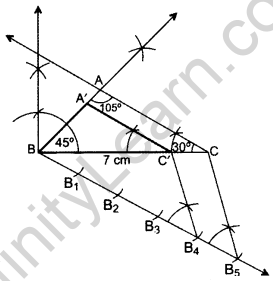
∴ A’BC’ is the required triangle.
Question 24.
Draw an isosceles ∆ABC in which BC = 5.5 cm and altitude AL = 3 cm. Then construct another triangle whose sides are \(\frac{3}{4}\) of the corresponding sides of ∆ABC. (2016OD)
Solution:
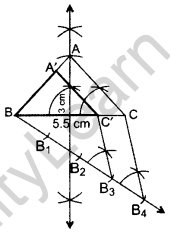
∴ ∆ABC’ is the required ∆.
Question 25.
Draw a triangle with sides 5 cm, 6 cm and 7 cm. Then draw another triangle whose sides are \(\frac{4}{5}\) of the corresponding sides of first triangle. (2016OD)
Solution:
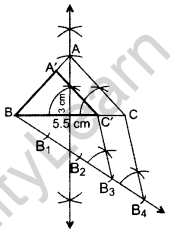
∴ ∆A’BC’ is the required ∆.
Question 26.
Draw two concentric cirlces of radii 3 cm and 5 cm. Construct a tangent to smaller circle from a point on the larger circle. Also measure its length. (2016D)
Solution:
We have, OD = 3 cm and OP = 5 cm
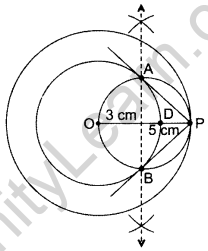
PA and PB are the required tangents
By measurement PA = PB = 4 cm.
Question 27.
Draw a circle of radius 4 cm. Draw two tangents to the circle inclined at an angle of 60° to each other. (2013, 2016OD)
Solution:
Draw a circle with O as centre and radius 4 cm.
Draw any ∠AOB = 120°. From A and B draw ∠PAO = ∠PBO = 90° which meet at P.
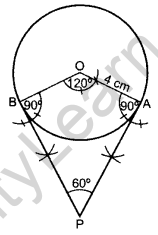
∴ PA and PB are the required tangents.



