Gravitation Class 9 Extra Questions Science Chapter 10

Gravitation Class 9 Extra Questions Very Short Answer Questions

Question 1. What will happen to the gravitational force between two bodies if the masses of one body is doubled?

Answer: If the mass of one body is doubled, force is also doubled.

Question 2. Why is ‘G’ called the universal gravitational constant?

Answer: The constant ‘G’ is universal because it is independent of the nature and sizes of bodies, the space where they are kept and at the time at which the force is considered.

Question 3. Who formulated the universal law of gravitation?

Answer: Isaac Newton

Question 4. How is gravitation different from gravity?

Answer: Gravitation is the force of attraction between any two bodies while gravity refers to attraction between any body and the earth.

Question 5. What does a small value of G indicate?

Answer: A small value of G indicates that the force of gravitational attraction between two ordinary sized objects is a very weak force.

Question 6. At what place on the earth’s surface is the weight of a body maximum?

Answer: At the poles.

Question 7. At what place on the earth’s surface is the weight of a body minimum?

Answer: At the equator.

Question 8. If the mass of a body is 9.8 kg on the earth, what would be its mass on the moon?

Answer: It will remain the same on the moon, i.e., 9.8 kg.

Question 9. Do fluids possess weight?

Answer: Yes, fluids have weight.

Question 10. Why can one jump higher on the surface of the moon than on the earth?

Answer: Because the value of acceleration due to gravity (g) on the moon’s surface is nearly l/6th to that of the surface of the earth.

Question 11. Define the standard kilogram.

Answer: The standard kilogram is the mass of a block of a platinum alloy kept at the international bureau of weights and measures near Paris in France.

Question 12. If the earth attracts two objects with equal force, can we say that their masses must be equal?

Answer: No

Question 13. Is weight a force?

Answer: Yes.

Question 14. What keeps the moon in uniform circular motion around the earth?

Answer: Gravitational force between moon and the earth keeps moon in uniform circular motion around the earth.

Question 15. When a body is dropped from a height, what is its initial velocity?

Answer: Zero.

Question 16. When a body is thrown vertically upwards, what is its final velocity?

Answer: Zero.

Question 17. Is the time taken by a body to rise to the highest point equal to the time taken to fall from the same height?

Answer: Yes.

Question 18. Is the acceleration due to gravity acting on a freely falling body directly proportional to the (a) mass of the body? (b) time of fall of the body?

Answer:

(a) No

(b) No

Question 19. Suppose gravity of earth suddenly becomes zero, then which direction will the moon begin to move if no other celestial body affects it? [NCERT Exemplar]

Answer: The moon will begin to move in a straight line in the direction in which it was moving at that instant because the circular motion of moon is due to centripetal force provided by the gravitational force of the earth.

Question 20. The earth is acted upon by gravitation of sun, even though it does not fall into the sun. Why? [NCERT Exemplar]

Answer: The gravitational force is responsible for providing the necessary centripetal force which allows the earth to move around the sun at the defined path or orbit. So, the earth does not fall into the sun.

Question 21. If the small and big stones are dropped from the roof of a house simultaneously, they will reach the ground at the same time. Why?

Answer: The acceleration due to gravity does not depend upon the mass of the stone or body. Both the bodies fall with the same acceleration towards the surface of the earth. Thus a big stone will fall with the same acceleration as a small stone. So, both the stones will reach the ground at the same time when dropped simultaneously.

Gravitation Class 9 Extra Questions Short Answer Questions-I

Question 1. The earth attracts an apple. Does the apple also attract the earth? If it does, why does the earth not move towards the apple?

Answer: According to Newton’s third law of motion, action and reaction are equal and opposite. It means that the force on the apple due to earth’s attraction is equal to that on the earth due to apple’s attraction. But we know, acceleration ∝ 1/m.

As the mass of the earth is very large as compared to that of the apple, the acceleration experienced by the earth will be so small that it will not be noticeable.

Question 2. Mention any four phenomena that the universal law of gravitation was able to explain.

Answer: The universal law of gravitation was able to explain successfully

• the force that binds us to the earth.
• the motion of the moon around the earth.
• the motion of planets around the sun.
• the tides due to the moon and the sun.

Question 3. When does an object show weightlessness?

Answer: Weightlessness is a state when an object does not weigh anything. It occurs only when a body is in a state of free fall under the effect of gravity alone.

Question 4. Why does a body reach the ground quicker at poles than at the equator when dropped from the same height?

Answer: The acceleration due to gravity is more at the poles than at the equator. The time taken for a body is less if the acceleration due to gravity is more when the initial velocities and the distance travelled are the same. So, when dropped from the same height a body reaches the ground quicker at the poles than at the equator.

Question 5. What is the source of centripetal force that a planet requires to revolve around the sun? On what factors does that force depend? [NCERT Exemplar]

Answer: Gravitational force. This force depends on the product of the masses of the planet and sun and the distance between them.

Gravitation Class 9 Extra Questions Short Answer Questions-II

Question 1. Suppose that the radius of the earth becomes twice of its original radius without any change in its mass. Then what will happen to your weight?

Answer: We know that F = \(\frac{G M m}{r^{2}}\) as weight of a body is the force with which a body is attracted towards the earth,

∴ W = \(\frac{G M m}{r^{2}}\)

If the radius of the earth becomes twice of its original radius, then

W = \(\frac{G M m}{(2 r)^{2}}\)

= \(\frac{G M m}{4 r^{2}}=\frac{W}{4}\)

i.e., weight will be reduced to one-fourth of the original.

Question 2. Prove that if the earth attracts two bodies placed at same distance from the centre of the earth with the same force, then their masses are equal.

Answer: Let P and Q be the two bodies, the mass of body P = m₁ And the mass of body Q=m₂

As per the universal law of gravitation, the force of attraction between the earth and the body P is given by, F_p = \(\frac{G \times M_{e} \times m_{1}}{R^{2}}\) …..(1)

Where, R is the distance of the body from the centre of the earth. Similarly, the force of attraction between the earth and the body Q is given by

F_Q = \(\frac{G \times M_{e} \times m_{2}}{R^{2}}\) …….(2)

Since, the two forces, i.e., F_p and F_Q are equal, thus from (1) and (2),

\(\frac{G \times M e \times m_{1}}{R^{2}}=\frac{G \times M_{e} \times m_{2}}{R^{2}}\)

⇒ m₁ = m₂

Question 3. Give three differences between acceleration due to gravity (g) and universal gravitational constant (G).

Answer:

Differences between g and G

Acceleration due to gravity (g)	Universal gravitational constant (G)
1. Acceleration due to gravity is the acceleration acquired by a body due to the earth’s gravitational pull on it. 2. g is a vector quantity. 3. It is different at different places on the surface of the earth. Its value also varies from one celestial body to another.	1. Gravitational constant is numerically equal to the force of attraction between two masses of 1 kg that are separated by a distance of 1 m. 2. G is a scalar quantity. 3. The ‘G’ is a universal constant, i.e., its value is the same (i.e. 6.7 × 10-11 Nm2 kg-2) everywhere in the universe.

Question 4. On the earth, a stone is thrown from a height in a direction parallel to the earth’s surface while another stone is simultaneously dropped from the same height. Which stone would reach the ground first and why? [NCERT Exemplar]

Answer: For both the stones

Initial velocity, u = 0

Acceleration in downward direction = g

Both stones will take the same time to reach the ground because the two stones fall from the same height.

Question 5. Calculate the average density of the earth in terms of g, G and R.

Answer: We know that g = \(\frac{G M}{R^{2}}\) or M = \(\frac{g R^{2}}{G}\)

⇒ Average density of the earth, D = \(\frac{\text { Mass }}{\text { Volume }}=\frac{g R^{2}}{G \times V e}\)

(Where V_e is the volume of the earth)

or D = \(\frac{g R^{2}}{G \frac{4}{3} \pi R^{3}}=\frac{3 g}{4 \pi G R}\)

Question 6. Prove that if a body is thrown vertically upward, the time of ascent is equal to the time of descent.

Answer: Upward motion

v = u + gt₁

0 = u – gt₁

t₁ = \(\frac{u}{g}\) …(1)

Downward motion

v = u + gt₂

v = 0 + gt₂

As the body falls back to the earth with the same velocity it was thrown vertically upwards.

∴ v = u

u = 0 + gt₂

t₂ = u/g …(2)

From (1) and (2), we get t₁ = t₂

⇒ Time of ascent = Time of descent

Question 7. Two objects of masses ml and m2 having the same size are dropped simultaneously from heights h₁ and h₂, respectively. Find out the ratio of time they would take in reaching the ground. Will this ratio remain the same if (i) one of the objects is hollow and the other one is solid; and (ii) both of them are hollow, size remaining the same in each case? Give reasons. [NCERT Exemplar]

Answer:

As u = 0, h₁ = \(\frac{1}{2} g t_{1}^{2}\)

h₂ = \(\frac{1}{2} g t_{2}^{2}\),

\(\frac{\iota_{1}}{t_{2}}=\sqrt{\frac{h_{1}}{h_{2}}}\)

Ratio will not change in either case because acceleration remains the same. In case of free fall acceleration does not depend upon mass and size.

Gravitation Class 9 Extra Questions Long Answer Questions

Question 1. Derive expression for force of attraction between two bodies and then define gravitational constant.

Answer: “Every body in the universe attracts every other body with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them.” Let us consider two bodies A and B of masses m₁ and m₂ which are separated by a distance r. Then the force of gravitation (F) acting on the two bodies is given by

F ∝ m₁ × m₂…(1) anc F ∝ \(\frac{1}{r^{2}}\) ..(2)

Combining (1) and (2), we get

F ∝ \(\frac{m_{1} \times m_{2}}{r^{2}}\)

or F = G × \(\frac{m_{1} m_{2}}{r^{2}}\) ……..(3)

where G is a constant known as universal gravitational constant.

Here, if the masses mx and m2 of the two bodies are of 1 kg and the distance (r) between them is 1 m, then putting m₁ = 1 kg, m₂ = 1 kg and r = 1 m in the above formula, we get

G = F

Thus, the gravitational constant G is numerically equal to the force of gravitation which exists between two bodies of unit masses kept at a unit distance from each other.

Question 2. Define acceleration due to gravity. Derive an expression for acceleration due to gravity in terms of mass of the earth (M) and universal gravitational constant (G).

Answer: The acceleration produced in the motion of a body falling under the force of gravity is called acceleration due to gravity. It is denoted by ‘g’.

The force (F) of gravitational attraction on a body of mass m due to earth of mass M and radius R is given by

F = \(G \frac{m M}{R^{2}}\) …..(1)

We know from Newton’s second law of motion that the force is the product of mass and acceleration.

∴ F = ma

But the acceleration due to gravity is represented by the symbol g. Therefore, we can write

F = mg …(2)

From the equation (1) and (2), we get

mg = \(G \frac{m M}{R^{2}}\) or g = \(\frac{G M}{R^{2}}\) …(3)

When body is at a distance V from centre of the earth then g = \(\frac{G M}{r^{2}}\)

Question 3. Show that the weight of an object on the moon is \(\frac{1}{6}\) th of its weight on the earth.

Answer: Suppose the mass of the moon is M_m and its radius is R_m. If a body of mass m is placed on the surface of moon, then weight of the body on the moon is

W_m = \(\frac{G M_{m} m}{R_{m}^{2}}\) …(1)

Weight of the same body on the earth’s surface will be

W_e = \(\frac{G M_{e} m}{R_{e}^{2}}\) …(2)

where M_e = mass of earth and R_e = radius of earth.

Dividing equation (1) by (2), we get

\(\frac{W_{m}}{W_{e}}=\frac{M_{m}}{M_{e}} \times \frac{R_{e}^{2}}{R_{m}^{2}}\) ….(3)

Now, mass of the earth, M_e = 6 × 10²⁴ kg

mass of the moon, M_m = 7.4 × 10²² kg

radius of the earth, R_e = 6400 km

and radius of the moon, R_m = 1740 km

Thus, equation (3) becomes,

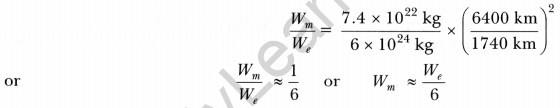
The weight of the body on the moon is about one-sixth of its weight on the earth.

Question 4. How does the weight of an object vary with respect to mass and radius of the earth? In a hypothetical case, if the diameter of the earth becomes half of its present value and its mass becomes four times of its present value, then how would the weight of any object on the surface of the earth be affected? [NCERT Exemplar]

Answer: Weight of an object is directly proportional to the mass of the earth and inversely proportional to the square of the radius of the earth, i.e.,

Weight of a body ∝ \(\frac{M}{R^{2}}\)

Original weight, W₀ = mg = mG \(\frac{M}{R^{2}}\)

When hypothetically M becomes 4 M and R becomes \(\frac{R}{2}\).

Then weight becomes W_n = mG \(\frac{4 M}{\left(\frac{R}{2}\right)^{2}}\) = (16 m G) \(\frac{M}{R^{2}}\) = 16 × W₀

The weight will become 16 times.

Helpful Resources

• NCERT Solutions for Class 9 Science
• NCERT Solutions for Class 9 Maths
• NCERT Solutions for Class 9 Social Science
• NCERT Solutions for Class 9 English

Numericals

Question 1. On the moon’s surface, the acceleration due to gravity is 1.67 ms^-2. If the radius of the moon is 1.74 × 10⁶ m, calculate the mass of the moon.
(G = 6.67 × 10¹¹ Nm²kg^-2)

Answer: Here, g = 1.67 ms^-2, R = 1.74 × 10⁶ m and G = 6.67 × 10^-2 Nm² kg^-2

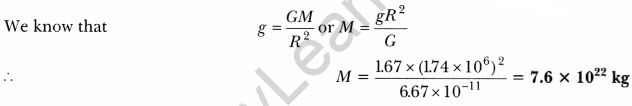
Question 2. A force of 20 N acts upon a body whose weight is 9.8 N. What is the mass of the body and how much is its acceleration? Take g = 9.8 m/s².

Answer: Weight, W = mg, m = \(\frac{W}{g}\), m = \(\frac{9.8}{9.8}\) = 1 kg

So, acceleration = \(\frac{\text { Force }}{\text { Mass }}=\frac{20}{1}\) = 20 m/s²

Question 3. A stone is dropped from a cliff. What will be its speed when it has fallen 100 m?

Answer:

Here, s = 100 m, u = 0

So, v² = u² + 2gs,

v² = 2gs = 2 × 9.8 × 100 = 1960

v = \(\sqrt{1960}\)m/s = 44.2 m/s

Question 4. From a cliff of 49 m high, a man drops a stone. One second later, he throws another stone. They both hit the ground at the same time. Find out the speed with which he threw the second stone.

Answer: For the first stone

u = 0 ms^-1, h = 49 m,

As we know s = ut + \(\frac{1}{2}\) gt²

∴ 49 = 0 × t + \(\frac{1}{2}\) × 9.8 × t²

⇒ t² = \(\frac{98}{9.8}\) = 10

⇒ t = \(\sqrt{10}\) = 3.16 s

i.e., First stone would take 3.16 s to reach the ground.

For the second stone, the time taken by the second stone to reach the ground is one second less than that taken by the first stone as both the stones reach the ground at the same time.

That is, for the second stone, t = (3.16 – 1)s = 2.16s

∴ For the second stone,

g = 9.8 ms^-2, h = 49 m, t = 2.16 s, u = ?

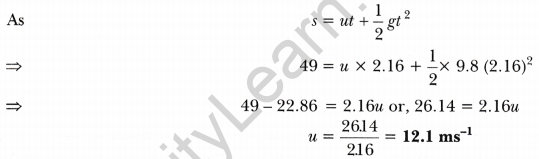
i.e., the second stone was thrown downward with a speed of 12.1 ms^-1.

Question 5. A stone is dropped from the top of a 40 m high tower. Calculate its speed after 2 s. Also find the speed with which the stone strikes the ground.

Answer:

(i) As v = u + gt

∴ v = 0 + (-10) × 2 = -20 ms^-1

(ii) As v = u² + 2 gs

or, v² – 0² = 2(-10) × (-40)

or, v = \(\sqrt{800}\)

= \(20 \sqrt{2}\)ms^-1

Question 6. Calculate the value of acceleration due to gravity g using the relation between g and G.

Answer: We know that G = 6.67 × 10^-11 Nm² kg^-2

Mass of the earth, M_e = 6 × 10²⁴ kg

And Radius of the earth, R_e = 6.4 × 10⁶ m

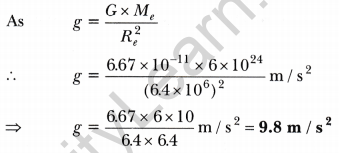
Question 7. Suppose the mass of the earth somehow increases by 10% without any change in its size. What would happen to your weight? Suppose the radius of the earth becomes twice of its present radius without any change in its mass, what will happen to your weight?

Answer:

(i) Original weight = \(\frac{G M m}{r^{2}}\), where M is the mass of the earth.

When M changes to new mass M’

New mass, M’=M + 10% of M

= M + \(\frac{10}{100}\)M = M + \(\frac{M}{10}\) = \(\frac{11M}{10}\) = 1.1 M

New weight becomes 1.1 times.

i.e., weight will increase by 10%.

(ii) Weight = \(\frac{G M m}{r^{2}}\), where r is the radius of the earth. When r changes to 2r, the new weight is given by

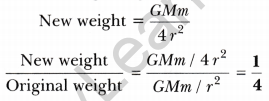
∴ New weight becomes 4 times.

Question 8. Two bodies of masses 3 kg and 12 kg are placed at a distance 12 m. A third body of mass 0.5 kg is to be placed at such a point that the force acting on this body is zero. Find the position of that point.

Answer: Given m₁ = 3 kg; m₂ = 12 kg

Let the mass, m₃ = 0.5 kg be placed at a distance of ‘x’ m from m₁, as shown in figure.

Then force acting on m₃ due to m₁, is equal and opposite to the force acting on m₃ due to m₂.

The position of required point is at a distance of 4 m from mass of 3 kg.

Question 9.
A stone dropped from the roof of a building takes 4s to reach the ground. Calculate the height of the building.
Answer:
Here, initial velocity, u = 0
Time taken to reach the ground, t = 4 s
Acceleration, a = g = 9.8 m/s²
Height of the building, h = ?

Question 10. A ball is thrown up with a speed of 0.5 m/s.

(i) How high will it go before it begins to fall?

(ii) How long will it take to reach that height?

Answer:

Initial speed, u = 0.5 m/s

Acceleration, g = – 9.8 m/s²

Final speed, v = 0

(i) We know v² – u²

= 0 – (0.5)² = 2 × (-9.8) × h

or – 0.25 = -19.6 h

or h = \(\frac{0.25}{19.6}\) = 0.0127 m

h = 1.27 cm

(ii) Putting the values in the formula v = u + gt0 = 0.5 – 9.8t

or t = \(\frac{0.5}{9.8}\) = 0.05 s

Question 11. Find the percentage change in the weight of a body when it is taken from the equator to the poles. The radius of the earth at the poles is 6357 km, the radius at the equator is 6378 km.

Answer:

% Variation in the weight of a body = % Change in g = 0.7%.

Gravitation Class 9 Extra Questions HOTS (Higher Order Thinking Skills)

Question 1. Why does formation of tides takes place in sea or ocean?

Answer: The tides in the sea formed by the rising and falling of water level in the sea are due to the gravitational force of attraction which the sun and the moon exert on the water surface in the sea.

Question 2. Why does a body orbiting in space possess zero weight with respect to a spaceship?

Answer: The astronaut and the spaceship are orbiting with same acceleration hence, the body does not exert any force on the sides of the spaceship. Therefore, the body appears to be floating weightlessly. It also implies that a body orbiting in space has zero weight with respect to a spaceship.

Question 3. Identical packets are dropped from two aeroplanes—one above the equator and other above the north pole, both at height h. Assuming all conditions to be identical, will those packets take same time to reach the surface of earth? Justify your answer. [NCERT Exemplar]

Answer: The value of ‘g’ at the equator of the earth is lesser than that at poles. Therefore, the packets fall slowly at equator in comparison to the poles. Thus, the packets will remain in air for longer time interval, when it is dropped at the equator.

Question 4. How does the force of attraction between the two bodies depend upon their masses and distance between them? A student thought that two bricks tied together would fall faster than a single one under the action of gravity. Do you agree with his hypothesis or not? Comment. [NCERT Exemplar]

Answer: F ∝ m,₁m₂ and F ∝ \(\frac{1}{r^{2}}\)

This hypothesis is not correct. The two bricks like a single body, fall with the same speed to reach the ground at the same time in case of free fall. This is because acceleration due to gravity is independent of the mass of the falling body.

Question 5. Velocity-time graph for the ball’s motion is shown in figure.

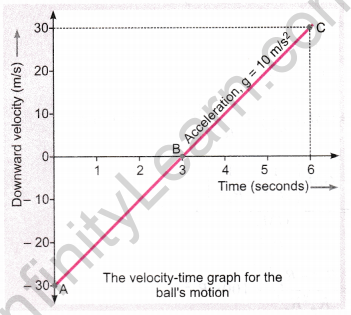
Observe the graph and answer the following questions.

Assume that g = 10 m/s² and that there is no air resistance.

(a) In which direction is the ball moving at point C?

(b) At which point is the bal 1 stationary?

(c) At which point is the bal 1 at its maximum height?

(d) What is the ball’s acceleration at point C?

(e) What is the ball’s acceleration at point A?

(f) What is the bal l’s acceleration at point B?

(g) At which point does the bal 1 have the same speed as when it was thrown?

Answer:

(a) Downward

(b) At point B

(c) At point B

(d) Acceleration = 10 ms^-2

(e) Acceleration = -10 ms^-2

(f) Acceleration = 10 ms^-2

(g) At point C