Table of Contents
Josef Stefan was an Austrian physicist who made significant contributions to understanding blackbody radiation. In 1879, he formulated Stefan’s Law, which states that the radiant energy of a blackbody is proportional to the fourth power of its temperature. This means that a perfect blackbody, an object that absorbs all radiation falling on it, emits more energy as it gets hotter. Stefan’s Law was a crucial step in studying blackbody radiation and paved the way for the quantum theory of radiation.
Stefan began his career as a lecturer in mathematical physics in 1858 and became a professor of physics in 1863. By 1866, he was the director of the Physical Institute at the University of Vienna. Five years later, he empirically derived Stefan’s Law, which was later theoretically confirmed by Ludwig Boltzmann. This combined work led to the law being named the Stefan-Boltzmann Law. Understanding “What is Stefan’s Law” helps us appreciate how energy emission changes with temperature.
Also Check: Wein’s Displacement Law
Stefan’s Law, also known as the Stefan-Boltzmann Law, explains the power radiated by a black body based on its temperature and surface area. Widely used in thermodynamics and astrophysics, Stefan’s Law helps us understand how objects like stars and planets emit radiation. Scientists use Stefan’s Law to study these celestial bodies and their behaviors. Additionally, Stefan’s Law has practical applications, such as in designing solar panels and other energy conversion devices. By applying Stefan’s Law, we can improve the efficiency of these technologies and gain deeper insights into the natural world.
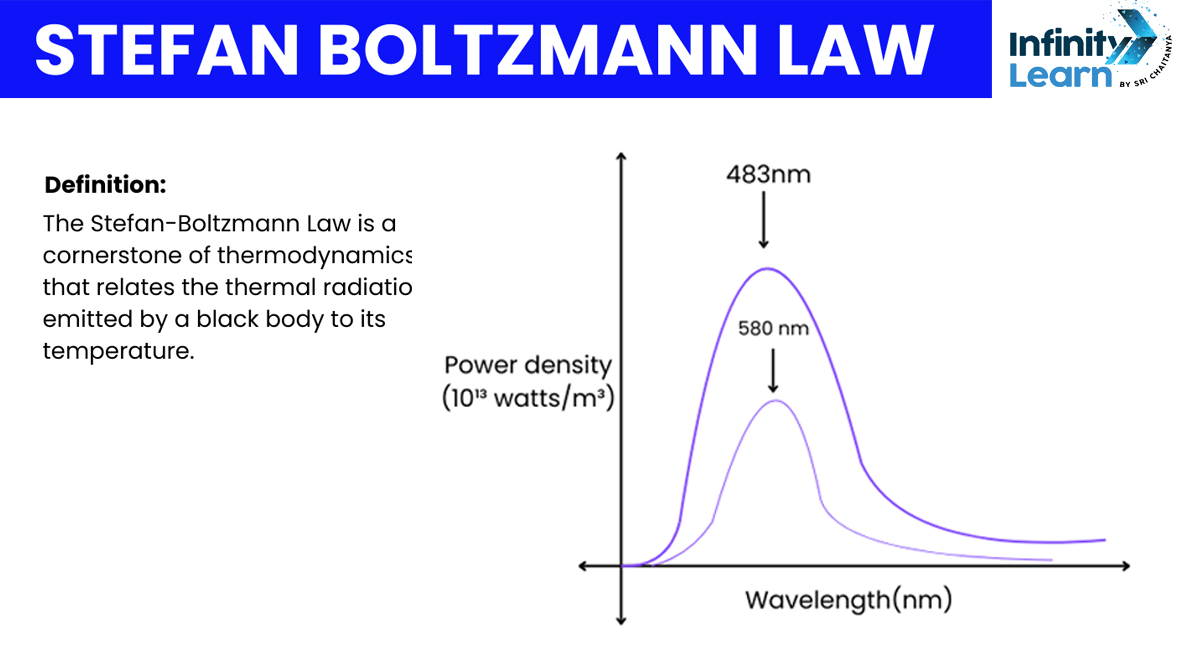
What is Stefan’s Law?
Stefan’s Law, also known as the Stefan-Boltzmann Law, states that the total energy emitted per unit surface area of a black body across all wavelengths per unit of time is directly proportional to the fourth power of the black body’s thermodynamic temperature and its emissivity. In simpler terms, Stefan’s Law explains that the power emitted by a black body increases rapidly with its temperature. This law highlights that as the temperature of a black body rises, the amount of energy it emits also increases significantly. Stefan’s Law is crucial for understanding the relationship between temperature and radiation in black bodies.
Stefan-Boltzmann Constant
The Stefan-Boltzmann Constant, named after physicists Josef Stefan and Ludwig Boltzmann, is a key component in Stefan’s Law. This constant, symbolized by the Greek letter σ, serves as the proportionality factor in Stefan’s Law.
Also Check: Ohm’s Law
Value of the Stefan-Boltzmann Constant
In the SI unit system, the value of the Stefan-Boltzmann Constant is approximately 5.67 × 10-8 watts per square meter per Kelvin to the fourth power (W/(m²K⁴)). Here are its values in different unit systems:
- SI Units: 5.670367 × 10-8 W/(m²K⁴)
- CGS Units: 5.6704 × 105 erg/(cm²s K⁴)
- Thermochemistry Units: 11.7 × 108 cal/(cm² day K⁴)
- U.S. Customary Units: 1.714 × 109 BTU/(ft² hr °R⁴)
The dimension of the Stefan-Boltzmann Constant is [M]1[L]0[T]-3[K]-4, representing mass (M), length (L), time (T), and temperature (K).
Understanding the Stefan-Boltzmann Constant is crucial for applying Stefan’s Law, which helps determine the radiant energy emitted by a blackbody based on its temperature.
Examples of Stefan’s Law
Welding
Welding is a process that joins two pieces of metal by heating them until they fuse together. During welding, sparks can be seen because energy is radiated into the surroundings. This demonstrates Stefan’s Law, which explains how energy is emitted as heat.
Calculating the Radius of Stars
The radius of a star can be calculated based on its luminosity, which is the total power radiated by the star into space. This power depends on the star’s surface area and temperature. Stefan’s Law shows the relationship between an object’s surface area, temperature, and the rate of radiation it emits, helping astronomers determine the size of stars.
Aluminium Foil
Aluminium foil is another example of Stefan’s Law in action. This law explains that objects with lower emissivity radiate less energy. Since aluminium foil has a low emissivity of about 0.1 units, it effectively keeps food warmer for longer periods by minimizing radiation loss.
These examples illustrate how Stefan’s Law applies to various real-world scenarios, from welding and astronomy to everyday uses like aluminium foil.
Also Check: Kirchoff’s Law
Understanding Stefan’s Law in Physics
Stefan’s Law, also known as the Stefan-Boltzmann Law, explains that the total radiant heat power emitted by a surface is proportional to the fourth power of its absolute temperature. The formula for Stefan’s Law is:
E=σT4
In this formula:
- E represents the radiant heat energy emitted per unit area per second.
- σ is the Stefan-Boltzmann constant.
- T is the absolute temperature.
Using Stefan’s Law, we can estimate the energy emitted by the Sun. Given the Sun’s photosphere temperature is around 6000 K, the energy emitted can be calculated as:
Esun=ϵσT4
Assuming
ϵ=1:
Esun=1×5.67×10−8×(6000)4
This results in an approximate energy emission of:
Esun≈25.12×109J m−2s−1
Stefan’s Law helps us understand the relationship between temperature and emitted radiation, providing insights into various physical phenomena.
Applications of Stefan-Boltzmann Law
Stefan’s Law, also known as the Stefan-Boltzmann Law, has many real-world applications. Here are a few important uses:
- Stefan’s Law helps scientists calculate the luminosity of celestial bodies such as stars, planets, and galaxies.
- The law is also used to understand how greenhouse gases affect our atmosphere. By using Stefan’s Law, scientists can calculate the amount of energy absorbed by the atmosphere and predict the impact of rising temperatures.
- Engineers apply Stefan’s Law to compare surface temperatures of different materials. This helps them design more power-efficient systems that do not require active cooling.
In these ways, Stefan’s Law plays a crucial role in astronomy, environmental science, and engineering.
Also Check: Charles Law
FAQs on Stefan’s Law
Who proposed Stefan's Law and when?
The Austrian physicist Josef Stefan proposed Stefan's Law in 1879.
Is the Stefan-Boltzmann law applicable to all bodies?
No, the Stefan-Boltzmann law is only applicable to black bodies, which are surfaces that can absorb all incident heat radiation.
What is the value of Stefan-Boltzmann’s constant?
In physics, the value of Stefan-Boltzmann’s constant is approximately 5.670374419 × 10−8 watts per meter² per Kelvin⁴.
How was the Stefan-Boltzmann constant discovered?
The Stefan-Boltzmann constant is named after Josef Stefan and Ludwig Boltzmann. Josef Stefan discovered this constant based on John Tyndall's 1864 measurements of infrared emissions from a platinum filament. In 1879, Stefan deduced the proportionality to the fourth power of absolute temperature from Tyndall’s work. Ludwig Boltzmann then derived the constant from theoretical principles in 1884, using the work of Adolfo Bartoli on radiation pressure and applying thermodynamics principles.
What is Stefan's Law?
Stefan's Law, or the Stefan-Boltzmann Law, states that the total energy emitted per unit time and per unit area of a blackbody is proportional to the fourth power of the blackbody's temperature.
How is the Stefan-Boltzmann constant derived?
One way to derive the Stefan-Boltzmann constant is by integrating Planck’s Radiation Formula.








