Table of Contents
A coin toss is a fundamental and widely known binary experiment in which a coin is flipped into the air and allowed to fall to the ground. The two possible outcomes of a coin toss are typically referred to as “heads” and “tails.” This simple and unpredictable act of tossing a coin has been historically used as a decision-making tool, determining outcomes in sports events, settling disputes, and even in games of chance.
Coin toss probability is based on the principle of equally likely outcomes, assuming a fair coin with unbiased results. The probability of each outcome (heads or tails) is 0.5 or 50%, as both are equally probable. A coin toss is a straightforward binary experiment with two possible outcomes: heads or tails. It is widely used for random decision-making and serves as a basic example to illustrate fundamental probability concepts. A coin toss’s simplicity and well-defined nature make it a popular starting point for introducing probability theory to students and researchers.
Sample Space for a Single Coin Toss
The sample space for a single coin toss consists of all the possible outcomes of the experiment. In this case, there are two possible outcomes: “heads” and “tails.” The sample space, S, can be represented as S = {H, T}, where H represents the event of getting heads and T represents the event of getting tails.
Coin Toss Probability
Probability measures the chances of an event to occur.
Now, in the case of coins,
As only two outcomes in a fair coin toss exist, both “heads” and “tails” have equal probabilities. Each outcome has a probability of 0.5 or 50%. Mathematically, P(H) = P(T) = 0.5.
| Number of possible outcomes | 2 |
| Number of outcomes to get head | 1 |
| Probability of getting a head | ½ |
Principle of Equally Likely Outcomes
Coin Toss Probability Formula
P(H) = Number of favorable outcomes (heads) / Total number of possible outcomes = 1/2 = 0.5
P(T) = Number of favorable outcomes (tails) / Total number of possible outcomes = 1/2 = 0.5
Sample Space and Probability of Multiple Coin Tosses
For example, when tossing a fair coin twice, the sample space includes four possible outcomes: {HH, HT, TH, TT}.
Each outcome has an equal probability of 0.25 or 25%.
Coin Toss Probability Formula: Solved Examples
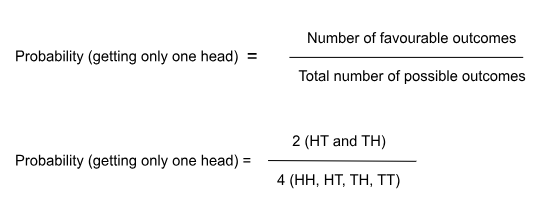
When tossing two fair coins simultaneously, there are four possible outcomes:
- HH (Head-Head)
- HT (Head-Tail)
- TH (Tail-Head)
- TT (Tail-Tail)
When 3 coins are tossed, the possible outcomes can be
{HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}.
Thus,
The total number of possible outcomes = 8.
Getting at least 2 heads includes {HHH, HHT, HTH, THH} outcomes.
So the number of desired outcomes = 4
Therefore,
the probability of getting at least 2 heads = 4/8 = ½ = 0.5Coin
FAQs on Toss Probability Formula
Is a coin flip actually 50-50?
A fair coin flip is 50-50, with equal chances of getting heads or tails. However, practical factors like weight distribution and flipping force may introduce minor biases.
What is a coin toss used for?
A coin toss is commonly used for random decision-making, settling disputes, choosing starting teams in sports, and making choices with two possible options.
Is a coin toss truly random?
A fair coin toss, under controlled conditions, is considered truly random due to the unpredictability of the coin's motion and external factors affecting the outcome.
How do I choose a coin toss?
To perform a coin toss, hold the coin between your thumb and index finger, then flip it into the air, allowing it to fall to the ground freely.
When three coins are tossed simultaneously, which coin is used for a toss in cricket?
In cricket, a special coin with one side featuring the cricket emblem and the other side featuring a country's emblem is used for the toss.
What are heads in a coin?
Heads is one of the two possible outcomes of a coin toss, usually represented by the side of the coin with a distinct design or image.









