Introduction to Eigenvalues and Eigenvectors

Linear transformations are crucial in mathematics and its applications, representing operations such as rotations, scaling, and shearing. When a linear transformation is applied to a vector, some special vectors remain unchanged in direction but only differ in scale by a scalar factor. These unique vectors are known as eigenvectors, and the scalar factor represents the eigenvalue associated with the eigenvector.

Definition of Eigenvalues and Eigenvectors

Formally, given a square matrix A, a non-zero vector v is an eigenvector of A if Av is a scalar multiple of v. The scalar multiple is denoted by λ and is known as the eigenvalue corresponding to the eigenvector v.
Mathematically, this relationship is expressed as Av = λv.

Eigenvalues are the solutions to the characteristic equation |A – λI| = 0, where I is the identity matrix.

Eigenvector Equation

The equation of the eigenvector is written as:
AX = λX

In the place of λ substitute the value of Eigenvalues, to get the corresponding Eigenvector.

Finding Eigenvalues and Eigenvectors

We follow a systematic process to determine the eigenvalues and eigenvectors of a square matrix.

• First, we find the characteristic polynomial by subtracting λI from the matrix A and computing its determinant.
• Next, we set the characteristic polynomial to zero and solve for λ, obtaining the eigenvalues.
• Subsequently, we find the eigenvectors by substituting each eigenvalue into the equation (A – λI)v = 0 and solving for v.

Properties of Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors possess several essential properties:

1. Eigenvalues can be real or complex: While some matrices have all real eigenvalues, others may have complex eigenvalues. The complex eigenvalues often come in conjugate pairs.
2. Multiplicity of eigenvalues: An eigenvalue may have a multiplicity greater than one, indicating the number of linearly independent eigenvectors corresponding to that eigenvalue.
3. Eigenvectors form a basis: If a square matrix has n distinct eigenvalues, then its n eigenvectors form a basis for the vector space in which they reside.
4. Diagonalization: Under certain conditions, a square matrix A can be diagonalized, which means expressing A in the form PDP^(-1), where D is a diagonal matrix containing the eigenvalues of A, and P is a matrix containing the corresponding eigenvectors.

Types of Eigenvector

The eigenvectors are of two types, namely,

1. Left Eigenvector
2. Right Eigenvector

Left Eigenvector

The left eigenvector is represented in the form of a row vector which satisfies the following condition:

AX_L=λX_L

Where,
A is a given matrix of order n, and λ is one of its eigenvalues.

X_L is a row vector of a matrix.

[ x₁ x₂ x₃ …. x_n]

Right Eigenvector

The right eigenvector is represented in the form of a column vector which satisfies the following condition:

AX_R = λX_R

Where,
A is a given matrix of order n, and λ is one of its eigenvalues.

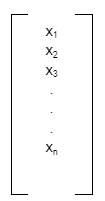
X_R is a column vector of a matrix. i.e.,

Maths Topics Math Articles Inverse of Matrices Types of Matrices

Applications of Eigenvalues and Eigenvectors

Eigenvalues and eigenvectors find significant applications in various practical fields, including:

1. Quantum Mechanics: In quantum mechanics, certain operators’ eigenvectors represent a quantum system’s possible states, and their corresponding eigenvalues represent the observable quantities.
2. Principal Component Analysis (PCA): In data analysis and machine learning, PCA uses eigenvectors to transform high-dimensional data into a lower-dimensional space while preserving the most significant information.
3. Structural Engineering: Eigenvalues and eigenvectors are employed to analyze structures’ stability and oscillation modes, such as buildings and bridges.
4. Image and Signal Processing: In image compression and signal filtering, eigenvectors represent data efficiently and denoise signals.
5. Quantum Computing: Quantum algorithms, such as Shor’s algorithm, leverage the concept of eigenvalues and eigenvectors to solve certain problems on quantum computers efficiently.

Eigenvalues and eigenvectors are powerful mathematical tools with diverse applications across multiple disciplines. Their ability to uncover fundamental properties of linear transformations, data analysis, and quantum systems makes them indispensable in modern scientific and technological advancements. Understanding eigenvalues and eigenvectors deepens our knowledge of linear algebra and enhances our problem-solving capabilities in various real-world scenarios.

FAQs on Eigenvalues and Eigenvectors

What is the significance of eigenvalues and eigenvectors in linear algebra?

Eigenvalues and eigenvectors help us understand how a linear transformation affects specific vectors, enabling us to identify stable directions of the transformation and their corresponding scaling factors.

How are eigenvalues and eigenvectors computed for a given matrix?

To compute eigenvalues, we find the solutions to the characteristic equation |A - λI| = 0, where A is the matrix and I is the identity matrix. Eigenvectors are obtained by solving the equation (A - λI)v = 0, where v is a non-zero vector, and λ is an eigenvalue.

Can a matrix have more than one eigenvalue?

Yes, a matrix can have multiple eigenvalues, each with its corresponding eigenvectors. The number of linearly independent eigenvectors associated with an eigenvalue is called its multiplicity.

Are eigenvalues always real numbers?

No, eigenvalues can be real or complex numbers. Some matrices have all real eigenvalues, while others may have complex eigenvalues, often in conjugate pairs.

What does it mean for a matrix to be diagonalizable using eigenvalues and eigenvectors?

A square matrix A is diagonalizable if expressed as PDP(-1), where D is a diagonal matrix containing the eigenvalues of A, and P is a matrix containing the corresponding eigenvectors. Diagonalization simplifies many computations involving the matrix.