Table of Contents
Symmetric matrix
Definition of a symmetric matrix: A square matrix A = [aij] is called a symmetric matrix if aij = aij, for all i,j values
Example of the symmetric matrix:
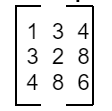
is an example of a symmetric matrix
Note: Matrix A is symmetric if A’ = A (where A’ is the transpose of the matrix)
Transpose of matrices
To understand if a matrix is a symmetric matrix, it is very important to know about the transpose of a matrix and how to find the transpose of a matrix.
If the rows and columns of an m×n matrix are interchanged to get an n × m matrix, the new matrix obtained is called the transpose of the given matrix.
Skew-Symmetric Matrix
Definition of Skew-symmetric matrix: A square matrix A = [aij] is a skew-symmetric matrix if aij = -aji, for all values of i,j.
If we put i=j, then,
aii = -aii
⇒ 2aii = 0
⇒ aii = 0
Thus, in a skew-symmetric matrix, all diagonal elements are zero.
Example of a Skew-symmetric matrix:
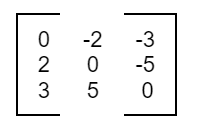
is an example of skew-symmetric matrices.
Note: A square matrix A is skew-symmetric if A’ = -A.
Properties of Symmetric and skew-symmetric matrices
- Every square Matrix can be uniquely expressed as the sum of a symmetric matrix and a skew-symmetric matrix.
- If A is a symmetric Matrix, then An, n belonging to the Natural number, will be symmetric.
- A is skew-symmetric, then An, n N will be symmetric if n is even, and An will be skew-symmetric if n is odd.
- Null Matrix is always symmetric and skew-symmetric.
- If A and B are both symmetric, then AB + BA will be symmetric, and AB – BA will be skew-symmetric.
What is the difference between a symmetric matrix and a skew-symmetric matrix?
A symmetric matrix and a skew-symmetric matrix are the square matrices. But the major difference between them is:
- The symmetric matrix equals its transpose.
⟹If A is a symmetric matrix, then A = AT - Whereas a skew-symmetric matrix is a matrix whose transpose equals its negative.
⟹If A is a skew-symmetric matrix, then AT = – A.
For better understanding of matrices, also read:
| Matrices | Eigenvalues of a symmetric matrix | Inverse of matrices |
| Determinants | Transpose of matrices | Types of matrices |
FAQs on Symmetric and Skew-symmetric Matrix
Can a matrix be both symmetric and skew-symmetric?
No, a matrix cannot be symmetric and skew-symmetric unless it is the null matrix (a matrix with zero elements). In a non-null matrix, the presence of non-zero diagonal elements in a symmetric matrix contradicts the property of having zero diagonal elements in a skew-symmetric matrix.
Are symmetric and skew-symmetric matrices always square matrices?
Both symmetric and skew-symmetric matrices are defined for square matrices only. In other words, their number of rows equals the number of columns.
Are the eigenvalues of a symmetric matrix real?
Yes, all eigenvalues of a symmetric matrix are real. This property is known as the spectral theorem for symmetric matrices.
What is the relationship between the eigenvectors of a symmetric matrix?
The eigenvectors corresponding to distinct eigenvalues of a symmetric matrix are orthogonal (perpendicular) to each other.
Can a matrix be both symmetric and diagonal?
A diagonal matrix where all non-diagonal elements are zero is symmetric and diagonal.
Can a matrix be both skew-symmetric and diagonal?
No, a matrix cannot be skew-symmetric and diagonal unless it is the null matrix. In a non-null matrix, the presence of non-zero diagonal elements contradicts the property of having zero diagonal elements in a skew-symmetric matrix.
How can we determine if a matrix is symmetric or skew-symmetric?
To determine if a matrix is symmetric, we compare it to its transpose. If the matrix is equal to its transpose (A = A'), it is symmetric. To determine if a matrix is skew-symmetric, we compare it to the negation of its transpose. If the matrix equals the negation of its transpose (A = -A'), it is skew-symmetric.








