Table of Contents
Transpose of a Matrix: Definition
The Transpose of a matrix is defined as the matrix received by interchanging the rows into columns or columns into rows of the initial matrix.
The transpose of the matrix is denoted by using the letter “T” in the superscript of the given matrix.
For example, if “A” is the given matrix, then the transpose of the matrix is represented by A’ or AT.
The general statement to represent the transpose of the matrix is written as:
If A = [aij]m×n
then A’= [aij]n×m
How to Find the Transpose of a Matrix?
To find a transpose of a matrix, we will consider an example,
If a matrix is a 2×3 matrix, i.e. it has 2 rows and 3 columns.
Therefore, to find the transpose of a matrix, the elements in the first row of the initial matrix are written in the first column of the new matrix. Similarly, the elements in the second row of the initial matrix are written in the second column of the new matrix.
Hence, the order of the new matrix becomes 3×2, as it has 3 rows and 2 columns.
For example:
Let the matrix A be:
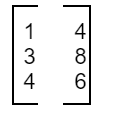
Therefore, the transpose of the matrix A (A’) is written as
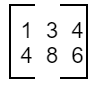
Therefore, the transpose of a matrix is given by interchanging rows and columns.
Properties of Transpose of a Matrix
The properties of the Matrices are mentioned below. Each property will be explained along with an example.
Transpose of the Transpose Matrix
If we take the transpose of the initial matrix A and name the obtained matrix as matrix B, then if we take the transpose of the second Matrix i.e. matrix B, the matrix now received will be equal to the initial matrix A.
Hence, for a matrix A,
(A’)’ = A
For example:
Let the matrix A be:

Therefore, the transpose of the matrix A (A’) is written as

Now retaking the transpose we get, The initial matrix again, i.e.

Addition Property of Transpose
The sum of the transpose of individual matrices A and B will be exactly equal to the transpose of an addition of two matrices A and B obtained
Example –
Let the matrix A and its transpose A’ be:

Now, let us suppose matrix B and its transpose B’ are:
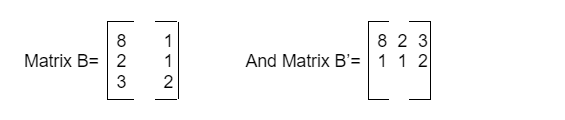
Now, the sum of matrix A and B and their transpose respectively are:
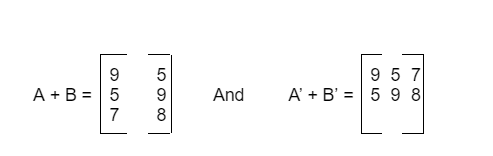
Now, transpose of A + B is:

Therefore, (A + B)’ = A’ + B’
So, we can observe that Addition property of transpose is proved.
(iii) Multiplication by Constant
If a matrix A is multiplied by any constant k and its transpose is taken, then the matrix obtained, say matrix B, is equal to the transpose of the original matrix multiplied by that constant.
Generalised representation for this property is:
(kA)’ = B = k(A’)
Example-
Let the matrix A multiplied by a constant k and its transpose B be:

Now,
Let the matrix A’ and k(A’) be:
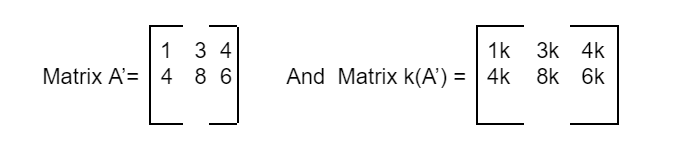
We can observe that (kA)’ = B = k(A’) is proven.
Frequently Asked Questions on Matrix Transpose
What is the transpose of a matrix?
The transpose of a matrix is obtained by interchanging its rows and columns. The elements in the original matrix's first row become the transpose's first column, and so on.
How is the transpose of a matrix denoted?
The transpose of a matrix A is denoted as A' or AT, with a superscript T.
Are there any other important properties of matrix transpose?
Yes, there are several other properties of matrix transpose, such as the distributive property, the transpose of a product of matrices, and the inverse of a transpose, among others.
Is the transpose of a matrix applicable to all matrices?
Yes, the transpose operation can be performed on any type of matrix, including square matrices, rectangular matrices, and even complex matrices.
How is the transpose of a matrix useful in mathematics and applications?
The transpose of a matrix finds applications in various areas, including linear algebra, matrix operations, systems of linear equations, data analysis, image processing, and computer graphics, among others. It allows for efficient manipulation and analysis of matrix data.








