Table of Contents
A Matrix is a rectangular array of m × n numbers, which may be either real or complex. These numbers are set in the form of m horizontal lines and n vertical lines and altogether defined as a matrix of order m by n, and also it is represented as m × n Matrix’. The rectangular array is enclosed in either () or [] brackets. This article will discuss the types of Matrices.
Types of Matrices
There are different types of Matrices based on the number of elements, the number of rows and columns or their order.
Different matrices based on the different factors are summarised in the table below.
| Type of Matrix | Details |
| Row Matrix | A = [aij]1×n |
| Column Matrix | A = [aij]m×1 |
| Zero or Null Matrix | A = [aij]mxn, where, aij = 0 |
| Singleton Matrix | A = [aij]mxn where, m = n =1 |
| Horizontal Matrix | [aij]mxn where n > m |
| Vertical Matrix | |
| Square Matrix | [aij]mxn where, m = n |
| Diagonal Matrix | A = [aij] when i ≠ j |
| Scalar Matrix | A = [aij]mxn [aij] = k when i = j [aij] = 0 when i ≠ j |
| Identity (Unit) Matrix | A = [aij]mxn where, [aij] = 1 when i = j [aij] = 0 when i ≠ j |
| Equal Matrix | A = [aij]mxn and B = [bij]rxs where, aij = bij, m = r, and n = s |
| Triangular Matrices | Can be either upper triangular (aij = 0, when i > j) or lower triangular (aij = 0 when i < j) |
| Singular Matrix | |A| = 0 |
| Non-Singular Matrix | |A| ≠ 0 |
| Symmetric Matrices | A = [aij] where, aij = aji |
| Skew-Symmetric Matrices | A = [aij] where, aij = aji |
| Hermitian Matrix | A = Aθ |
| Skew – Hermitian Matrix | Aθ = -A |
| Orthogonal Matrix | A AT = In = AT A |
| Idempotent Matrix | A2 = A |
| Involuntary Matrix | A2 = I, A-1 = A |
| Nilpotent Matrix | ∃ p ∈ N such that AP = 0 |
Types of Matrices
On the basis of the number of rows and columns, the matrices are classified as:
- Row Matrices
- Column Matrices
- Square Matrices
Row Matrix
A matrix consisting of only one row is a row matrix.
Thus A = [aij]mxn is a row matrix if m = 1.
This matrix is called a Row matrix because it has only one row, and the order of a row matrix will hence be 1 × n.
For example,
A = [8 9 7 6] is a row matrix of order 1 x 4.
Column Matrix
A matrix consisting of only one column is a column matrix.
Thus, A = [aij]mxn is a column matrix if n = 1. Hence, the order is m × 1.
For example,
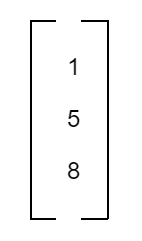
is a column matrix of order 3 x 1.
Square Matrix
If the matrix has an equal number of rows and the number of columns, then it is called a square matrix.
Thus, A = [aij]mxn is a square matrix if m = n.
For example,
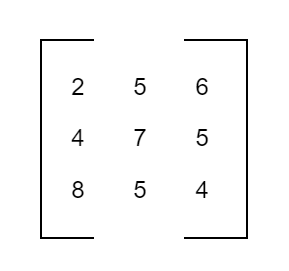
is a square matrix of order 3 × 3.
Trace of matrix: The sum of the diagonal elements in a square matrix A is called the trace of matrix A, and which is denoted by tr(A).
On the basis of the value entered in the row and column, the matrices are classified as:
Zero or Null Matrix
The matrix with all the elements as zero is called a zero matrix and is generally denoted by 0.
Thus, A = [aij]mxn is a zero-matrix if aij = 0 for all i and j.
For example,
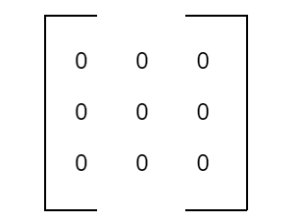
is a zero matrix of 3 x 3 order.
Singleton Matrix
If the matrix has a single element, it is called a singleton matrix.
Thus, A = [aij]mxn is a singleton matrix if m = n = 1.
For example:
[8], [9], [a], [ ] are singleton matrices.Horizontal Matrix
A matrix of m x n order is defined as a horizontal matrix if n > m.
For example,
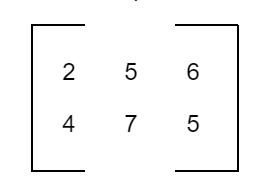
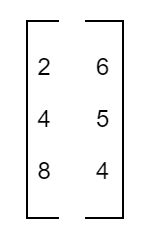
Vertical Matrix
A matrix of order m x n is defined as a vertical matrix if m > n.
For example,
Diagonal Matrix
If all the elements of the square matrix except the principal diagonal are zero, then it is said to be a diagonal matrix.
Thus, a square matrix A = [aij] is a diagonal matrix if aij = 0,when i ≠ j.
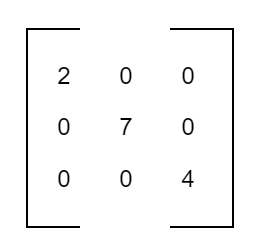
is a diagonal matrix of order 3 x 3.
Students must note that:
- A diagonal matrix will always be a square matrix.
- The diagonal elements are characterised by aij in general where i = j.
- Also, a diagonal matrix can have only a single diagonal.
Scalar Matrix
If all the elements in the diagonal of a diagonal matrix are equal, it is called a scalar matrix. Thus, a square matrix
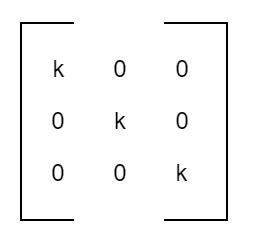
where k is a constant.
Also, it is wondered, what if all the diagonal elements are equal to 1? Will this kind of Matrix be a scalar or diagonal matrix?
The answer to this query is quite simple, this type of Matrix will still be a scalar matrix and obviously a diagonal matrix too. These matrices are known as the identity matrix.
Unit Matrix or Identity Matrix
If all the elements of a principal diagonal in a diagonal matrix are 1, it is called a unit matrix.
A unit matrix of order n is denoted by In.
For example:
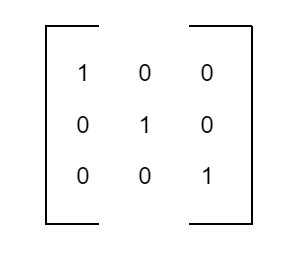
To conclude,
- All identity matrices are always scalar matrices
- All scalar matrices are precisely diagonal matrices
- All diagonal matrices are basically square matrices
- Also note that the converse of the above mentioned statements is not true for any of the cases.
Equal Matrices
Equal matrices are those matrices which are equal in terms of their elements.
The conditions for matrix equality are discussed below.
Equality of Matrices Conditions:
Two matrices A and B are said to be equal if they are of the same order and their corresponding elements are equal, i.e. two matrices A = [aij]m×n and B = [bij]r×s are equal if:
- m = r, i.e., the number of rows in A = the number of rows in B.
- n = s, i.e. the number of columns in A = the number of columns in B
- aij = bij, for i = 1, 2, ….., m and j = 1, 2, ….., n, i.e. the corresponding
elements are equal;
For example, Matrices
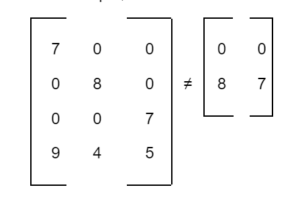
are not equal because their orders are not the same.
But, If
Matrix A
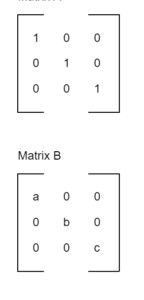
Matrix A and B are equal matrices then,
a=1, b=1, c=1
Triangular Matrix
A square matrix is said to be a triangular matrix if the elements above or below the principal diagonal are zero, and there are of two types:
-
Upper Triangular Matrix
A square matrix [aij] is called an upper triangular matrix, if aij = 0, when i > j is an upper triangular matrix of order 3 x 3.
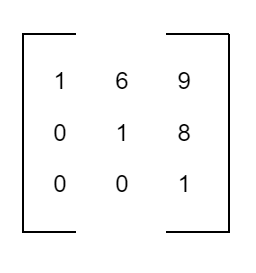
-
Lower Triangular Matrix
A square matrix is called a lower triangular matrix, if aij = 0 when i < j.
is a lower triangular matrix of order 3 x 3.
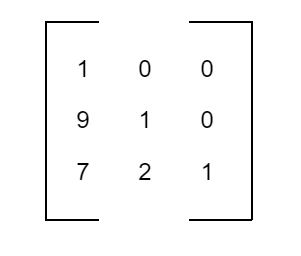
Singular Matrix and Non-Singular Matrix
- Matrix A is said to be a singular matrix if it’s determinant |A| = 0
- Matrix A is said to be a singular matrix if it’s determinant |A| ≠ 0
Symmetric and Skew Symmetric Matrices
Symmetric matrix:
A square matrix A = [aij] is called a symmetric matrix if aij = aji, for all i,j values;
Eg.
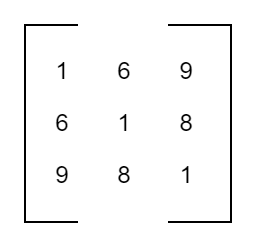
is symmetric
Note: matrix A is symmetric if A’ = A (where ‘A’ is the transpose of the matrix)
Skew-Symmetric Matrix
A square matrix A = [aij] is a skew-symmetric matrix if aij = aji, for all
values of i,j.
[putting j = i] aii = 0Thus, in a skew-symmetric matrix, all diagonal elements are zero.
E.g.
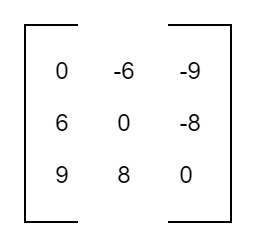
are skew-symmetric matrices.
Note: A square matrix A is a skew-symmetric matrix A’ = -A.
Some Important Conclusions on Symmetric and Skew-Symmetric Matrices
- any square matrix,
- then A + A’ is a symmetric matrix
- And, A – A’ is a skew-symmetric matrix.
- Every square matrix can be uniquely expressed as the sum of a symmetric and skew-symmetric matrix.
- If A and B are symmetric matrices, then A & B commute, i.e. AB is symmetric AB = BA.
- The matrix B’AB is symmetric or skew-symmetric in correspondence if A is symmetric or skew-symmetric.
- All positive integral powers of a symmetric matrix are symmetric.
- Positive odd integral powers of a skew-symmetric matrix are skew-symmetric, and positive even integral powers of a skew-symmetric matrix are symmetric.
Also, Orthogonal Matrix, Idempotent Matrix, Involuntary Matrix and Nilpotent Matrix are the special matrices whose conditions are mentioned below.
| Orthogonal Matrix | A AT = In = AT A |
| Idempotent Matrix | A2 = A |
| Involuntary Matrix | A2 = I, A-1 = A |
| Nilpotent Matrix | ∃ p ∈ N such that AP = 0 |
FAQs on Types of Matrices
What is a square matrix?
A square matrix is a matrix with an equal number of rows and columns. In other words, it has the same number of rows as columns. For example, a 3x3 matrix or a 5x5 matrix is a square matrix.
What is a diagonal matrix?
A diagonal matrix is a square matrix where all the elements outside the main diagonal (the diagonal from the top left to the bottom right) are zero. The main diagonal elements can be any values, including zero.
What is a symmetric matrix?
A symmetric matrix is a square matrix that is equal to its transpose. In other words, if A is a symmetric matrix, then A^T = A. This means that the elements above and below the main diagonal are mirror images of each other.
What is a skew-symmetric matrix?
A skew-symmetric matrix is a square matrix where the transpose of the matrix is equal to the negation of the matrix. In other words, if A is a skew-symmetric matrix, then A^T = -A. This means that the elements above the main diagonal are the negations of the elements below the main diagonal.








