Table of Contents
Introduction to Volume of Cylinder
The volume of a cylinder can be calculated using the formula: V = πr²h, where V represents the volume, π (pi) is a constant approximately equal to 3.14159, r is the radius of the base of the cylinder, and h is the height of the cylinder.
Definition of Cylinder
A cylinder is a three-dimensional geometric shape characterized by its high volume and two parallel circular bases of equal size. It can be defined as a solid figure with straight sides and a constant cross-sectional circular shape throughout its length.
What is Volume?
The volume of a 3-dimensional shape is the amount of space it occupies. It can also be defined as the amount of space contained within the solid.
What is the volume of a cylinder?
The volume of a cylinder is a fundamental concept in geometry that measures the amount of space enclosed by a cylinder. A cylinder is a three-dimensional geometric shape with two parallel circular bases and a curved surface connecting the bases. It is often encountered in real-life objects such as cans, pipes, and containers.
The volume of a cylinder is the measure of space it occupies and can be found using the formula: V = πr²h, where V represents volume, π (pi) is approximately 3.14159, r is the radius of the base, and h is the height of the cylinder.
It is the product of the area of its circular base and its height.
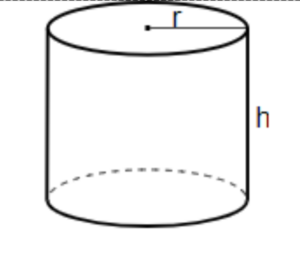
Volume of cylinder
For a cylinder with r as the radius of its circular base and h as height,
Volume of Cylinder Formula
Volume of cylinder = Area of circular base x Height
Volume of cylinder = πr2 x h
In this formula, “π” represents the mathematical constant pi, which is approximately 3.14159. “r” denotes the radius of the circular base of the cylinder, and “h” represents the height of the cylinder. The radius is the distance from the center of the circular base to its edge, while the height is the perpendicular distance between the two bases.
To find the volume, we square the radius (r²) and multiply it by the height (h) and the value of pi (π). This formula holds true for cylinders of any size or proportions.
It is important to note that the units used for the radius and height must be consistent. For example, if the radius is measured in centimeters, the height should also be in centimeters to obtain the volume in cubic centimeters.
The volume of a cylinder is significant in various applications. For instance, it helps determine the capacity of cylindrical containers, calculate the amount of liquid or gas that can be stored, and understand the displacement of fluids in engineering and physics. Additionally, the volume of a cylinder is a fundamental concept in solid geometry and plays a crucial role in understanding the properties and relationships of three-dimensional shapes.
Volume of Cylinder in Litres
The Volume of a Cylinder in Litres refers to the capacity or space enclosed by a cylinder and is typically measured in liters. It is calculated using the formula V = πr²h, where V represents volume, π is approximately 3.14159, r is the radius of the cylinder’s base, and h is its height. The result is expressed in liters, a unit of measurement for volume.
Volume of Hollow Cylinder
The volume of a hollow cylinder is the measure of the space inside the cylinder with an empty center. To calculate it, you subtract the volume of the inner cylinder from the volume of the outer cylinder. The formula for the volume of a hollow cylinder is V = πh(R² – r²), where V represents the volume, π (pi) is approximately 3.14159, h is the height, R is the outer radius, and r is the inner radius of the hollow cylinder.
Volume of Hollow Cylinder Formula
The formula for calculating the volume of a hollow cylinder is:
V = πh(R² – r²)
Volume of a Right Circular Cylinder Formula
The formula for the volume of a right circular cylinder is:
V = πr²h
In this formula, V represents the volume, π (pi) is approximately 3.14159, r is the radius of the circular base, and h is the height of the cylinder.
Solved examples on Volume of Cylinder
Example 1. Find the volume of a cylinder with a radius of 4 cm and a height of 10 cm.
Solution:
Using the formula for the volume of a cylinder: Volume = π x r² x h
Given:
Radius (r) = 4 cm
Height (h) = 10 cm
Substituting the given values into the formula:
Volume = π x (4 cm)² x (10 cm)
Volume = 3.14159 x 16 cm² x 10 cm
Volume = 502.65408 cm³ (rounded to five decimal places)
Therefore, the volume of the cylinder is approximately 502.65408 cm³.
Example 2. A cylindrical water tank has a diameter of 1.5 meters and a height of 2 meters. Calculate the volume of the tank.
Solution:
First, we need to find the radius since the diameter is given. The radius (r) is half the diameter.
Given:
Diameter = 1.5 meters
Height (h) = 2 meters
Calculating the radius:
Radius (r) = Diameter / 2 = 1.5 meters / 2 = 0.75 meters
Using the volume formula:
Volume = π x r² x h
Substituting the values:
Volume = 3.14159 x (0.75 meters)² x 2 meters
Volume = 3.14159 x 0.5625 square meters x 2 meters
Volume = 3.534291 square meters x 2 meters
Volume = 7.068582 cubic meters
Therefore, the volume of the cylindrical water tank is approximately 7.068582 cubic meters.
| Check Related Volumes of Cylinders | |
| Volume of a Cone Formula | Volume of a Pyramid Formula |
| Volume of a Prism | Volume of a Right Circular Cylinder |
Frequently asked questions on Volume of Cylinder
Sphere's volume is 4/3 times pi times radius cubed. Cone's volume is 1/3 times pi times radius squared times height. Cylinder's volume is pi times radius squared times height.
Cuboid's volume is length times width times height.
A cube has equal sides. A cylinder has a top and bottom circle with a curved side.
Cube's volume is side length cubed. Cylinder's volume is pi times radius squared times height.
Cuboid's volume is length times width times height. Cylinder's volume is pi times radius squared times height.
The volume of a sphere is calculated using the formula 4/3 pi times the cube of its radius. This means you multiply the radius by itself three times and then multiply by both 4/3 and pi.
The volume of a cylinder is determined by multiplying pi by the square of its radius and then by its height. It's like finding the area of the circular base and then extending it up through the height of the cylinder.
To find the volume of a cone, you use 1/3 pi times the square of its radius times its height. Essentially, it's like finding the volume of a cylinder but taking only a third of it because a cone tapers to a point.
If we have a cylinder with a radius of 3 units and a height of 5 units, we first find the area of the circular base (pi times 3^2) and then multiply it by the height (5). The result is approximately 141.37 cubic units. What is the volume of sphere, cone, and cylinder?
What is the volume of the cuboid?
What is a cube and cylinder?
What is the formula for cube and cylinder?
What is the cuboid and cylinder formula?
What is the volume of the sphere?
What is a formula for cylinder?
What is a formula of cone?
What is the volume of a cylinder example?







