Table of Contents
Volume of a Pyramid Formula
Introduction:
The volume of a pyramid represents the amount of space enclosed by the pyramid. It can be thought of as the number of unit cubes that can fit inside the pyramid. Pyramids are polyhedrons characterized by their polygonal base. They come in various forms, such as triangular, square pyramid, rectangular pyramid, and pentagonal pyramids, named after the shape of their base. In a pyramid, all the lateral faces are triangles, with one side of each triangle connecting to a side of the base.
What is Pyramid?
A pyramid is a polyhedron with one base that is any polygon. Its other faces are triangles.
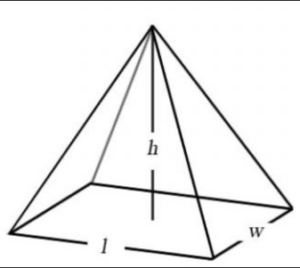
What is the formula for Volume of Pyramid?
The volume of a pyramid is a measure of the space enclosed by the pyramid. The formula to calculate the volume of a pyramid is given by:
Volume = (1/3) x base area x height
In this formula, the base area refers to the area of the base of the pyramid, and the height is the perpendicular distance from the base to the apex of the pyramid. The factor of 1/3 comes from the relationship between the volume of a pyramid and a prism with the same base and height.
For the above figure, base area will be w x l
Therefore, Volume = l x w x h
It is important to note that the base area should be measured in square units consistent with the units of length used for the height. The resulting volume will be expressed in cubic units.
The volume of a pyramid can be applied to various real-life scenarios, such as calculating the volume of a triangular roof, determining the capacity of a pyramid-shaped container, or estimating the amount of material needed to construct a pyramid-like structure.
When solving problems involving the volume of a pyramid, it is crucial to ensure that the measurements used for the base area and height are accurate and in the same units. By plugging in the appropriate values into the formula, one can easily calculate the volume and obtain a quantitative measure of the space occupied by the pyramid.
Solved Examples on Volume of Pyramid Formula:
Example 1: Find the volume of a triangular pyramid with a base area of 48 square units and a height of 10 units.
Solution:
The formula for the volume of a pyramid is V = (1/3) × base area × height.
Substituting the given values, we have V = (1/3) × 48 × 10 = 160 cubic units.
Therefore, the volume of the triangular pyramid is 160 cubic units.
Example 2: A square pyramid has a base side length of 6 units and a height of 8 units. Calculate its volume.
Solution:
The base area of a square pyramid is given by the formula A = side length².
So, the base area is A = 6² = 36 square units.
Using the volume formula V = (1/3) × base area × height, we get V = (1/3) × 36 × 8 = 96 cubic units.
Hence, the volume of the square pyramid is 96 cubic units.
Example 3: Determine the volume of a pentagonal pyramid with a base perimeter of 30 units and a height of 12 units.
Solution:
The formula for the base area of a regular pentagon is A = (5/4) × side length² × cot(π/5).
Given the base perimeter as 30 units, each side length of the pentagon is 30/5 = 6 units.
Plugging the values into the volume formula V = (1/3) × base area × height, we get V = (1/3) × [(5/4) × 6² × cot(π/5)] × 12.
Calculating further, we find V ≈ 88.29 cubic units.
Hence, the volume of the pentagonal pyramid is approximately 88.29 cubic units.
More Related Formulas
| Trapezoid formula | Diagonal of a Cube Formula |
| Parallelogram Formula | Percentage Increase Formula |
| Polynomial Formula | Cp Formula |
| Ratio Formula | Square Root Formula |
| Surface Area of a Cylinder Formula | Frequency Distribution Formula |
Frequently Asked Questions on Volume of Pyramid Formula:
How do you find the volume area of a pyramid?
To find the volume of a pyramid, use the formula V = (1/3) × base area × height. The base area is determined by the shape of the base (e.g., A = s² for a square base or A = (1/2) × b × h for a triangular base). Substitute the values into the formula and multiply the base area by (1/3) to get the volume. Ensure that the base area and height are measured in the same units.
What is the volume of a 3-sided pyramid?
To find the volume of a 3-sided pyramid, you need to know the base area and the height of the pyramid. The formula for the volume of a pyramid is V = (1/3) × base area × height. If you have the base area and height of the 3-sided pyramid, substitute these values into the formula and calculate the volume.
What is the volume of a pyramid with a square base?
The volume of a pyramid with a square base can be calculated using the formula V = (1/3) × base area × height. Since the base of the pyramid is square, the base area can be found by squaring the length of one side of the square. Once the base area and height are known, substitute these values into the formula to find the volume of the pyramid.
What is the volume of a pyramid with a rectangular base?
The volume of a pyramid with a rectangular base can be calculated using the formula V = (1/3) × length × width × height, where length and width are the dimensions of the base, and height is the perpendicular distance from the base to the apex (top) of the pyramid.
What is a half pyramid?
A half pyramid, also known as a right pyramid, is a pyramid that has its apex directly above the center of its base. It is called a half pyramid because it is formed by removing the top portion of a full pyramid. In a half pyramid, all the triangular faces are right triangles, and the base can be any polygon, such as a square, rectangle, or triangle. The height of the half pyramid is the perpendicular distance from the apex to the base.
What is a 4-sided pyramid called?
A four-sided pyramid is called a tetrahedron. It is a type of polyhedron with four triangular faces, four vertices, and six edges. The tetrahedron is the simplest and most basic type of pyramid, and it is often represented as a regular tetrahedron where all the faces are equilateral triangles. The tetrahedron is a three-dimensional shape with a unique and symmetric structure.
What's a 7-sided pyramid called?
A seven-sided pyramid is called a heptagonal pyramid. It is a polyhedron with a heptagonal (seven-sided) base and triangular faces that converge at a common vertex. The heptagonal pyramid is a specific type of pyramid that has a base with seven equal sides and seven equal angles. It is a unique geometric shape with distinct properties and characteristics.
How to find volume of pyramid with slant height?
To find the volume of a pyramid with the slant height, you will need additional information such as the base area or the height. The slant height alone is not sufficient to calculate the volume. If you have the base area and the slant height, you can use the formula V = (1/3) × base area × height, where the height can be determined using the Pythagorean theorem with the slant height and the height of the triangular face. If you have the height and the slant height, you can use the formula V = (1/3) × base area × height, where the base area can be determined using the formula for the area of the base shape (e.g., square, rectangle, triangle) depending on the type of pyramid. In summary, to find the volume of a pyramid with the slant height, you need either the base area or th







