Table of Contents
Introduction to Differentiation Formula
Differentiation formulas are fundamental tools in calculus, used to find the derivative of a function with respect to its independent variable. The derivative represents the rate of change or slope of the function at any given point. Key differentiation formulas include the
power rule (d/dx(x^n) = nx^(n-1)),
constant multiple rule (d/dx(kf(x)) = k*f'(x)), and sum/difference rule (d/dx(f(x) ± g(x)) = f'(x) ± g'(x)). These formulas enable us to analyse the behaviour of functions, find critical points, and solve optimization problems. Understanding differentiation is crucial for grasping fundamental concepts in calculus and various other mathematical disciplines.
First principle of differentiation
- The first principle of differentiation, also known as the “first principle of derivatives” or “limit definition of the derivative,” is the fundamental concept used to find the derivative of a function. It involves calculating the derivative from scratch using the definition of the derivative.
The first principle of differentiation is given by the following formula:
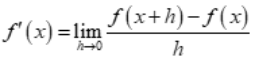
where f'(x) represents the derivative of the function f(x) with respect to x, and “limh→0” denotes the limit as the change in x (h) approaches zero.
In simple terms, the first principle measures the rate of change of a function f(x) at a specific point x by evaluating the slope of the tangent line to the curve at that point. By taking the limit as h approaches zero, we get the instantaneous rate of change, which is the derivative of the function at that point. The first principle forms the foundation of calculus and provides a rigorous way to calculate derivatives of functions..
List of rules of differentiation:
The list of some of the key rules of differentiation, which are used to find the derivative of a function:
- Constant Rule: d/dx (c) = 0, where c is a constant.
- Power Rule: d/dx (x^n) = n * x^(n-1), where n is a constant.
- Constant Multiple Rule: d/dx (k * f(x)) = k * d/dx (f(x)), where k is a constant.
- Sum/Difference Rule: d/dx (f(x) ± g(x)) = d/dx (f(x)) ± d/dx (g(x)).
- Product Rule: d/dx (f(x) * g(x)) = f'(x) * g(x) + f(x) * g'(x).
- Quotient Rule: d/dx (f(x) / g(x)) = [g(x) * f'(x) – f(x) * g'(x)] / [g(x)]^2.
- Chain Rule: d/dx (f(g(x))) = f'(g(x)) * g'(x).
Differentiation of algebraic functions
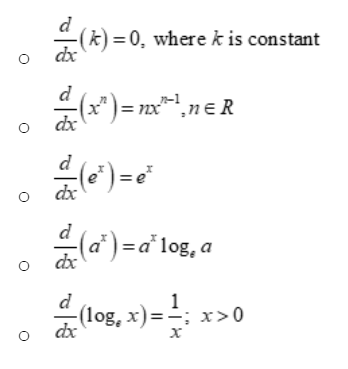
Differentiation of trigonometric functions
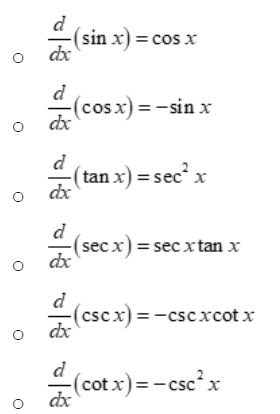
Differentiation of inverse trigonometric functions
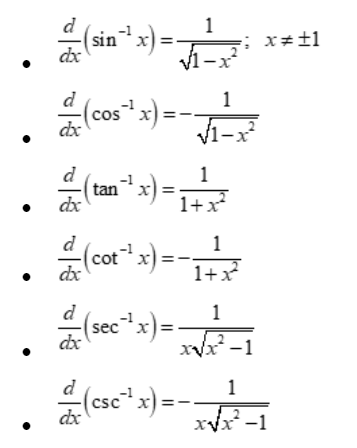
| Also Check | |
| Perimeter of Rectangle | Distance Formula |
| Volume Of A Cylinder Formula | Volume Formulas |
| Basic Math Formulas | Circumference Formula |
| Perimeter of Rhombus Formula | Rhombus Formula |
| Surface Area Formulas | Equilateral Triangle Formula |
| Integrals Formulas | Radius Formula |
| Trapezoid formula | Diagonal of a Cube Formula |
Frequently asked questions on Differentiation formula
What are three methods of differentiation?
Three methods of differentiation commonly used to find derivatives of functions are: Direct Application of Differentiation Rules: This method involves applying the basic rules of differentiation, such as the power rule, sum/difference rule, product rule, quotient rule, chain rule, and more, to find the derivative of a given function. Implicit Differentiation: This method is used when a function is implicitly defined by an equation, and it might not be straightforward to express y explicitly as a function of x. By differentiating both sides of the equation with respect to x and isolating the derivative of y, one can find the derivative. Logarithmic Differentiation: This technique is useful for differentiating complicated functions, especially those involving products, powers, and exponential functions. It involves taking the natural logarithm of both sides of the equation and then differentiating implicitly. These methods provide valuable tools for calculating derivatives and are essential in understanding the behavior of functions in calculus and various mathematical applications.
What is chain rule?
The chain rule is a fundamental rule of differentiation in calculus. It is used to find the derivative of a composite function, where one function is nested inside another. The chain rule allows us to differentiate the outer function and the inner function separately and then multiply their derivatives together Mathematically, if we have a composite function y = f(g(x)), where f(u) and g(x) are both differentiable functions, then the chain rule states: dy/dx = dy/du * du/dx. In words, the derivative of y with respect to x is equal to the derivative of y with respect to u (dy/du) multiplied by the derivative of u with respect to x (du/dx). The chain rule is a powerful tool that enables us to find derivatives of complex functions by breaking them down into simpler components. It plays a crucial role in many areas of mathematics, physics, engineering, and other sciences.
What is UV rule?
Let's use U and V as functions in the product rule. If we have a function of the form y = U(x) * V(x), where both U(x) and V(x) are differentiable functions, then the product rule states: d/dx (U(x) * V(x)) = U'(x) * V(x) + U(x) * V'(x). In words, to find the derivative of the product of two functions, we take the derivative of the first function (U'(x)) and multiply it by the second function (V(x)). Then, we add the original first function (U(x)) multiplied by the derivative of the second function (V'(x)). Using U and V as functions, the product rule allows us to differentiate the product of two functions more effectively.
What is the derivative of 2x?
The derivative of 2x with respect to x can be found using the power rule, which states that the derivative of x^n is n * x^(n-1). In this case, n = 1, and we have: d/dx (2x) = 2 * x^(1-1) = 2 * x^0 = 2. So, the derivative of 2x with respect to x is simply 2.
What is the Differentiation Formula?
The Differentiation Formula is a mathematical expression used to calculate the derivative of a function. It helps in finding the rate at which a function is changing at any given point. Commonly, the Differentiation Formula is represented as f′(x)
How is the Differentiation Formula applied in calculus?
In calculus, the Differentiation Formula is applied to determine the slope of a function at a specific point. By using the Differentiation Formula, you can find the instantaneous rate of change, which is crucial for understanding various physical and geometrical phenomena.
What are the basic rules of the Differentiation Formula?
The basic rules of the Differentiation Formula include the power rule, product rule, quotient rule, and chain rule. Each rule provides a method for finding the derivative of different types of functions. For example, the power rule in the Differentiation Formula is given by dxd (xn)=nxn−1.
Can you provide an example of using the Differentiation Formula?
Certainly! Consider the function f(x)=3x2+2x+1. Using the Differentiation Formula, the derivative f′(x) is found by applying the power rule: f′(x)=6x+2. This shows how the Differentiation Formula helps to find the rate of change of the function
Why is understanding the Differentiation Formula important?
Understanding the Differentiation Formula is important because it is a fundamental concept in calculus that has wide applications in science, engineering, and economics. The Differentiation Formula helps in analyzing and solving problems related to motion, optimization, and change, making it an essential tool for various fields.









