Volume of Cone Formula
The volume of a cone is a measurement that quantifies the amount of space occupied by the cone. A cone is a three-dimensional geometric shape with a circular base and a pointed top called the apex. The volume of a cone can be calculated using a specific formula.
Note that the formula for the volume of a cone is derived from the formula for the volume of a cylinder, as both shapes share a similar base and height relationship. The volume of a cone is given by the formula:
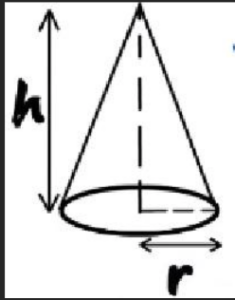
Cone
Volume = (1/3) x π x r2 x h
Where:
- Volume is the space occupied by the cone.
- π (pi) is a mathematical constant approximately equal to 3.14159.
- r is the radius of the circular base of the cone.
- h is the height of the cone, measured from the apex to the base.
To find the volume of a cone, square the radius (r) and multiply it by the height (h). Then, multiply the result by 1/3 and π. This formula can be applied to cones of any size or dimensions.
The volume of a cone is typically measured in cubic units, such as cubic centimetres (cm³) or cubic meters (m³). It is a fundamental concept in geometry and is used in various real-life applications, such as calculating the volume of ice cream cones, traffic cones, or the displacement of liquids in cone-shaped containers.
Remember, when working with the volume of a cone, ensure that the radius and height are measured using the same unit of measurement to maintain consistency.
Solved Examples on Volume of Cone:
Example 1. Find the volume of a right circular cone whose height and slant height are 4 m and 5 m respectively.
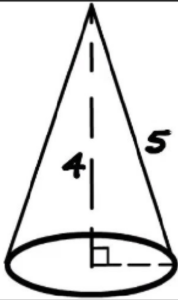
Figure 1
Solution:
Height of the cone (h) = 4 m
Slant height of the cone (l) = 5 m
Let r be the radius of the circular base of the cone. By Pythagoras theorem,
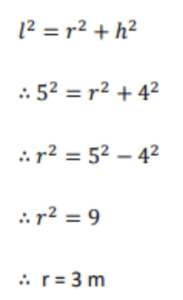
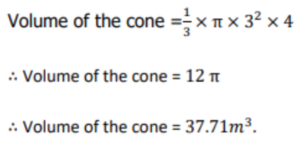
Thus, the volume of the right circular cone of height 4 m and slant height 5 m is 37.71 cubic
metres.
Example 2. Find the volume of a cone with a radius of 4 cm and a height of 6 cm.
Solution:
Using the formula for the volume of a cone:
Volume = (1/3) x π x r2 x h
Substituting the given values:
Volume = (1/3) x π x (4 cm)2 x 6 cm
= (1/3) x π x 16 cm2 x 6 cm
= (1/3) x π x 96 cm3
= 32π cm3 (approximately 100.53 cm3)
Therefore, the volume of the cone is approximately 32π cm3 or 100.53 cm3.
Frequently Asked questions on Volume of Cone:
- What is the volume of a cone?
Answer: The volume of a cone is the amount of space occupied by the cone. It is a measure of the three-dimensional capacity of the cone.
- How do you find the volume of a cone?
Answer: The volume of a cone can be calculated using the formula: Volume = (1/3) x π x r2 x h, where r is the radius of the base and h is the height of the cone.
- What are the units of volume for a cone?
Answer: The units of volume for a cone can be cubic units, such as cubic centimetres (cm³), cubic meters (m³), cubic inches (in³), etc.
- Can the volume of a cone be zero?
Answer: Yes, the volume of a cone can be zero if the height or the radius of the cone is zero. In such cases, the cone collapses to a point or a line, and it does not occupy any space.
- How is the volume of a cone related to the volume of a cylinder?
Answer: The volume of a cone can be derived from the volume of a cylinder. If the height of a cylinder is equal to the slant height of a cone, and the base radius of the cylinder is equal to the base radius of the cone, then the volume of the cone is one-third the volume of the cylinder.
- Can the volume of a cone be used to calculate its surface area?
Answer: No, the volume of a cone alone cannot be used to calculate its surface area. The surface area of a cone requires additional information, such as the slant height or the base radius.
- Can the volume of a cone be expressed in terms of its base area and height?
Answer: Yes, the volume of a cone can be expressed as V = (1/3) x base area x height, where the base area is the area of the circular base of the cone.
- How is the volume of a cone affected if the dimensions of the cone are doubled?
Answer: If the dimensions of a cone, such as the radius and height, are doubled, the volume of the cone will increase by a factor of 8 (2^3) since volume is proportional to the cube of the dimensions.





