Table of Contents
Introduction to Integral formulas
Integral formulae are key tools in calculus, used to calculate areas under curves, volumes of solids, and a variety of other things. Calculus’ basic theorem relates integrals with derivatives, making integral evaluation easier. The power rule, substitution rule, and integration by parts are all important formulae. Understanding and using these principles enables pupils to solve a wide range of mathematical problems.
Integral formulae for algebraic functions
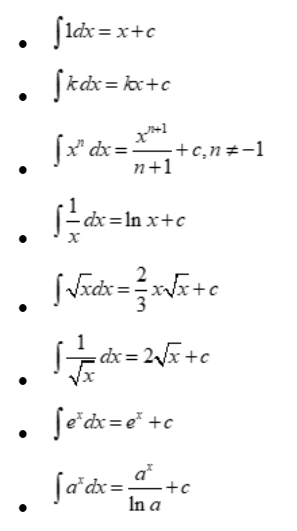
Rules for integration:
Here are some common integration formulas for algebraic functions:
Power Rule:
- ∫ x^n dx = (x^(n+1))/(n+1) + C, where n ≠ -1.
Constant Multiple Rule:
- ∫ k * f(x) dx = k * ∫ f(x) dx, where k is a constant.
Sum/Difference Rule:
- ∫ [f(x) + g(x)] dx = ∫ f(x) dx + ∫ g(x) dx.
Integration by Parts:
- ∫ u dv = u * v – ∫ v du, where u and v are differentiable functions.
These formulas are just a few examples of the wide range of algebraic functions that can be integrated. Integrating more complex functions may require using multiple techniques and approaches..
Integral formulae for Trigonometric functions:
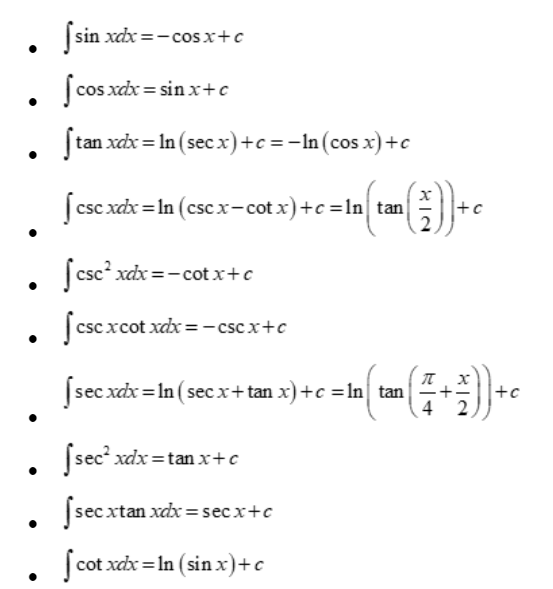
Integration of hyperbolic function

Integration of rational functions
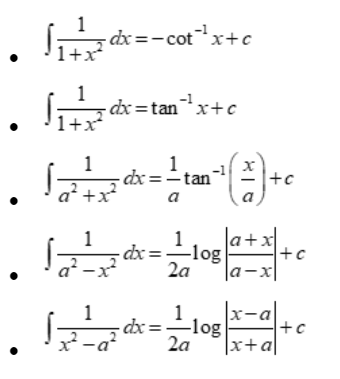
Integration of irrational function
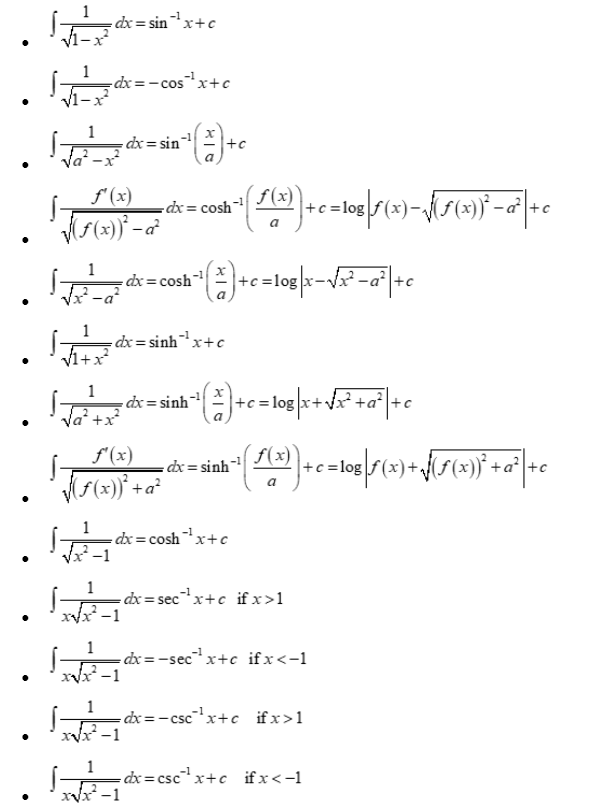
Special integrals
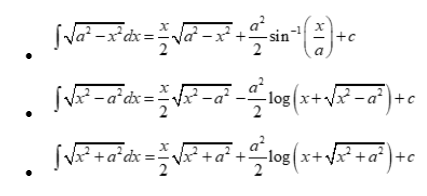
Integration by substitution related formula
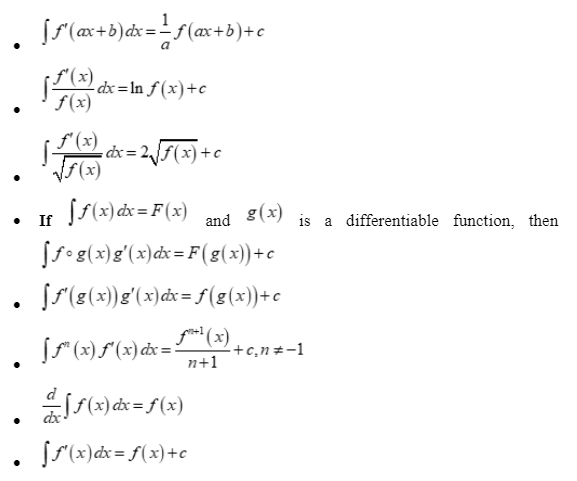
Integration formula by partial fractions
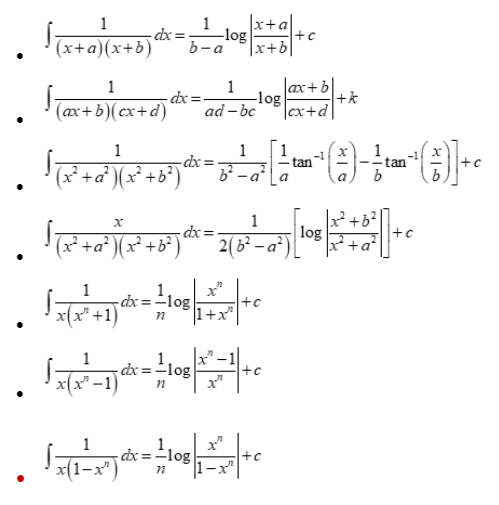
Also read: Math Formulas
Integration by parts:
If f(x), g(x) are any two functions, then
∫f(x).g(x)dx = f(x)∫g(x)dx – ∫f'(x)∫g(x)dxdx
Proper choice of first and second function
- The first function is the function which comes first in the word ILATE
- If one of the two functions is not directly integrable, then take this function as the first function.
- If one of the function is not directly integrable, and there is no other function, then unity is taken as the second function.
Some Integral formulas using integration by parts
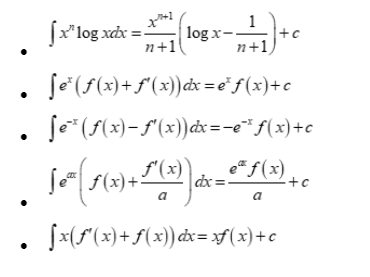
Integration formula for inverse trigonometric functions
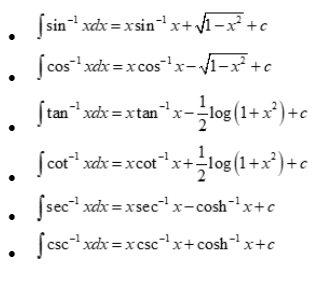
Solved examples which including integration formulas
Solve some examples using the integration formulas mentioned earlier.
Example 1: ∫ (3x^2 + 2x + 1) dx
Using the Power Rule:
∫ (3x^2) dx = (3 * x^(2+1))/(2+1) + C
= (3/3) * x^3 + C
= x^3 + C.
Using the Power Rule:
∫ (2x) dx = (2 * x^(1+1))/(1+1) + C
= x^2 + C.
Using the Power Rule:
∫ (1) dx = x + C.
Putting it all together:
∫ (3x^2 + 2x + 1) dx = x^3 + x^2 + x + C.
Example 2: ∫ (e^x + 5sin(x)) dx
Using the Exponential Integral:
∫ e^x dx = e^x + C.
Using the Trigonometric Integral:
∫ sin(x) dx = -cos(x) + C.
Since the integral of a sum is the sum of integrals:
∫ (e^x + 5sin(x)) dx = (e^x + C) + 5*(-cos(x) + C)
= e^x – 5cos(x) + C.
Example 3: ∫ (x^3 + 2x^2 – 2x + 5) dx
Using the Power Rule:
∫ (x^3) dx = (x^(3+1))/(3+1) + C = (1/4) * x^4 + C.
Using the Power Rule:
∫ (2x^2) dx = (2 * x^(2+1))/(2+1) + C = (2/3) * x^3 + C.
Using the Power Rule:
∫ (-2x) dx = -2 * (x^(1+1))/(1+1) + C = -x^2 + C.
Using the Power Rule:
∫ (5) dx = 5 * x + C.
Putting it all together:
∫ (x^3 + 2x^2 – 2x + 5) dx = (1/4) * x^4 + (2/3) * x^3 – x^2 + 5x + C.
These are just a few examples to illustrate the use of integration formulas. Remember, integration can involve more complex functions and may require multiple steps or special techniques in some cases.
| Also Check | |
| Perimeter of Rectangle | Distance Formula |
| Volume Of A Cylinder Formula | Volume Formulas |
| Basic Math Formulas | Circumference Formula |
| Perimeter of Rhombus Formula | Rhombus Formula |
| Surface Area Formulas | Equilateral Triangle Formula |
| Perimeter of a Parallelogram Formula | Radius Formula |
| Trapezoid formula | Diagonal of a Cube Formula |
| Percentage Increase Formula | |
Frequently asked questions on Integration formulas
What is the integration formula?
A mathematical statement that allows us to compute the antiderivative of a given function is known as an integration formula. When the derivative of the original function is known, it aids in determining the original function. Integration allows the computation of areas, volumes, and other important quantities in calculus by employing various integration rules and procedures.
What is dx in integration?
In integration, the symbol dx represents the differential of the variable x. It is an infinitesimal change in the independent variable x. The process of integration involves finding the antiderivative of a function with respect to x, and the 'dx' in the integral notation indicates that the integration is being performed with respect to 'x.' The 'dx' notation is used to specify the variable of integration and is a fundamental part of the integral calculus notation. It allows us to find the area under a curve, calculate accumulated quantities, and solve a wide range of mathematical problems.
What is called integration?
Integration is a fundamental concept in calculus, and it refers to the process of finding the antiderivative of a function. It is the reverse operation of differentiation. When we integrate a function, we determine another function whose derivative is equal to the original function. Integration is used to calculate areas under curves, volumes of solids, and to solve various mathematical problems in physics, engineering, economics, and other fields. It plays a crucial role in understanding the behavior of functions and their cumulative effects.
Why is integration used?
Integration is used for a variety of reasons in mathematics, science, and engineering due to its versatile applications: Area Calculation: Integration finds the area under curves, helping measure irregular regions. Volume Calculation: It determines volumes of complex 3D shapes. Accumulated Quantities: Integration calculates total change, like distance traveled, profit, or mass, based on rates of change. Physics and Engineering: Used to calculate work, energy, electric charge, fluid flow, moments of inertia, and centroids. Probability and Statistics: Employed in probability density functions and cumulative distribution functions. Differential Equations: It helps solve differential equations that model various phenomena. Economics and Finance: Used in economic models, pricing financial derivatives, and finance calculations. Signal Processing: Employed to calculate accumulated signal values over time. Optimization: It helps find maximum and minimum values of functions, aiding in optimization problems. Integration is a powerful tool, crucial for understanding real-world phenomena and solving a wide range of problems.
What are the rules of integration?
The rules of integration, also known as integration techniques or methods, are essential tools in calculus used to find antiderivatives and solve integrals. Improper Integrals: Used to evaluate integrals with infinite limits or unbounded functions. These rules, along with other specialized techniques, allow us to evaluate a wide range of integrals and solve diverse mathematical problems.









