Table of Contents
Introduction to Linear programming
Linear programming is a sophisticated mathematical approach for optimising solutions to a wide range of real-world situations. It entails maximising or minimising a linear objective function while keeping linear limitations in mind. Applications span from industrial resource allocation to logistical planning. The method employs graphical and algebraic methodologies to select the best viable solution from a set of options, offering useful insights for decision-making processes..
What is linear programming
Linear programming is a mathematical optimisation approach that seeks to maximise or minimise a linear objective function that is constrained by a linear function. It is widely used in resource allocation, production planning, and logistics. Linear programming finds the best solution among viable choices using graphical and algebraic approaches. It assists organisations and industries in making informed decisions by translating real-world issues into mathematical models, therefore increasing efficiency and effectiveness..
Components of linear programming:
Linear programming includes the following components:
- A linear equation reflecting the aim to maximise or minimise, commonly stated as a combination of choice variables, is an objective function.
- Variables representing the quantities to be determined or optimised in the issue are known as decision variables.
- Constraints: A collection of linear inequalities or equations that specify the decision variables’ constraints or restrictions.
- The set of possible solutions is represented by the region defined by the intersection of all restrictions.
- The best possible solution that maximises or minimises the goal function.
- Non-negativity The condition that decision variables be non-negative (greater than or equal to zero) is one of the constraints.
These elements combine to produce a linear programming issue, which is then solved mathematically to discover the best solution.
Characteristics of linear programming
- Technique for mathematical optimisation.
- Linear equation to maximise or minimise the objective function.
- Decision variables: These are the quantities to be optimised.
- Linear inequalities or equations serve as constraints.
- Intersection of constraints defines the feasible region.
- Optimal option: The best option that is achievable.
- Graphical and algebraic approaches were employed.
- It may be used in resource allocation, logistics, and other areas.
- It aids in decision-making and efficiency improvement.
- Mathematically models real-world problems.
Methods to solve the linear programming problems
To handle linear programming issues, there are two basic approaches:
- Graphical technique (for two variables) and the
- Simplex method (for many variables).
Linear programming simplex method
For problems with multiple variables, the simplex method is used to iteratively find the optimal solution by moving from one vertex (corner point) of the feasible region to another.
Example:
Maximize Z = 4x + 3y
Subject to:
2x + y ≤ 8
x + 2y ≤ 6
x, y ≥ 0
Solution:
Step 1: Convert the inequalities into equations (equalities) by introducing slack variables.
2x + y + s1 = 8
x + 2y + s2 = 6
Step 2: Set up the initial Simplex Table:
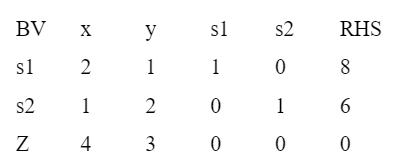
Step 3: Perform iterations to find the optimal solution.
Choose the most negative value in the Z-row as the pivot column.
Divide the corresponding RHS value by the pivot column value to determine the pivot row.
Perform elementary row operations to make the pivot element 1 and other elements in the pivot column zero.
Repeat these steps until all values in the Z-row are non-negative.
After iterations, the optimal solution is found as x = 2, y = 2, and Z = 14.
Linear programming graphical method
This method is suitable for problems with only two decision variables. It involves plotting the constraints on a graph and visually identifying the optimal solution.
Example:
Maximize Z = 3x + 2y
Subject to:
2x + y ≤ 10
x + 2y ≤ 8
x, y ≥ 0
Solution:
Step 1: Plot the feasible region determined by the constraints.
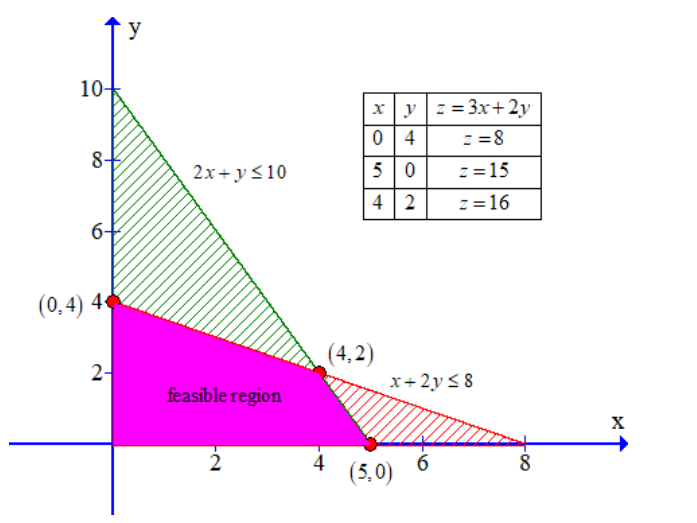
Step 2: Calculate the value of the objective function (Z) at each corner point of the feasible region.
Corner Points:
A (0, 4) => Z = 3(0) + 2(4) = 8
B (4, 2) => Z = 3(4) + 2(2) = 16
C (5, 0) => Z = 3(5) + 2(0) = 15
Step 3: Identify the corner point with the highest Z value; it corresponds to the optimal solution.
The optimal solution is at point B (4, 2), where Z = 16
Also Check For:
Applications of linear programming
Linear programming finds applications in various fields due to its ability to optimize solutions subject to linear constraints. Here are some common applications with explanations:
- Resource Allocation: Linear programming is extensively used in industries to allocate limited resources, such as labor, raw materials, and machine hours, to maximize production output while minimizing costs. It helps in determining the optimal mix of resources to achieve the desired production levels efficiently.
- Production Planning: Manufacturing companies use linear programming to plan their production schedules, taking into account constraints like available production time, labor, and inventory levels. By optimizing the production process, companies can increase productivity and reduce wastage.
- Transportation and Logistics: Linear programming is applied in optimizing transportation routes, vehicle assignment, and distribution of goods to minimize transportation costs while meeting demand requirements. This ensures efficient delivery and reduces overall transportation expenses.
- Financial Portfolio Optimization: In finance, linear programming helps investors optimize their portfolios by allocating investments among different assets. It considers risk factors, expected returns, and investment constraints to achieve a balanced and optimal portfolio.
- Marketing Campaigns: Linear programming aids marketers in budget allocation for advertising and promotion campaigns. It identifies the most effective combination of media channels and budget allocation to reach the target audience with the highest impact.
- Agricultural Planning: Farmers can use linear programming to optimize their crop planting decisions by considering factors such as available land, water resources, and crop yields. It enables them to maximize their profits and minimize the use of resources.
- Project Scheduling: Linear programming is applied in project management to optimize project schedules and resource allocation. It helps in identifying the critical path, resource constraints, and the most efficient project completion timeline.
- Diet Planning: Linear programming can be used to create optimal diet plans that meet nutritional requirements while minimizing costs. It is useful in planning menus for large institutions like hospitals, schools, or military bases.
- Blending Problems in Manufacturing: In industries like chemical engineering and food processing, linear programming is used to determine the optimal mix of ingredients or raw materials to achieve desired product specifications at minimum cost.
- Game Theory: Linear programming finds applications in game theory for solving two-person zero-sum games, such as chess or poker, to find optimal strategies for each player.
These applications demonstrate the versatility and practical significance of linear programming in various industries and decision-making processes, helping businesses and individuals make informed choices and improve overall efficiency.
Importance of linear programming
The importance of linear programming lies in its wide range of applications and its ability to optimize solutions effectively. Here are the key points highlighting its significance:
- Optimization: Linear programming allows for the optimization of resources, costs, and profits, leading to better decision-making and improved efficiency.
- Resource Allocation: It helps in allocating scarce resources efficiently, ensuring maximum utilization and minimal wastage.
- Complex Problem Solving: Linear programming can handle complex real-world problems by converting them into mathematical models and finding optimal solutions.
- Quantitative Decision-Making: It provides a structured and quantitative approach to decision-making, reducing reliance on intuition or guesswork.
- Strategic Planning: Businesses can use linear programming to develop strategic plans, considering various constraints and objectives.
- Cost Reduction: By optimizing processes and resource allocation, linear programming can lead to cost reduction and increased profitability.
- Logistics and Supply Chain Management: It aids in optimizing transportation routes, inventory management, and supply chain operations, resulting in smoother operations and reduced costs.
- Risk Management: In finance, it helps in managing risks associated with investments and portfolio management.
- Scheduling and Time Management: Linear programming assists in scheduling tasks, activities, and projects to optimize time utilization and meet deadlines efficiently.
- Improved Productivity: By identifying the most efficient use of resources, it contributes to improved productivity and output.
- Data-Driven Decision Making: Linear programming relies on data and mathematical models, promoting data-driven decision-making for better outcomes.
- Competitive Advantage: Businesses that use linear programming to optimize their operations gain a competitive advantage by becoming more efficient and cost-effective.
Overall, linear programming plays a crucial role in modern problem-solving, planning, and decision-making processes across various industries, helping organizations achieve their objectives while making the best use of available resources.
Frequently asked questions about Linear programming
What is linear programming and example?
Linear programming is a mathematical approach for solving problems that have linear constraints. It entails maximising or minimising a linear objective function that is constrained by linear inequality. A manufacturing business, for example, might utilise linear programming to identify the ideal production mix of multiple goods while taking resource limits and profit targets into account, resulting in efficient resource allocation and greater profitability.
What are three steps of linear programming?
The three steps of linear programming are as follows: Defining the Objective Function: Create a linear equation that represents the aim to maximise or minimise Creating Constraints: Create linear inequalities or equations that indicate the decision variables' constraints. To discover the best practicable solution that optimises the objective function within the restrictions, use mathematical approaches such as graphical analysis or the simplex algorithm.
What are five types of linear programming?
Maximisation: The goal is to maximise the value of the linear objective function while keeping restrictions in mind. Minimization: Within the specified limitations, the goal is to minimise the value of the linear objective function. movement: The optimisation of products movement from numerous sources to various destinations while minimising transportation expenses. Assignment is concerned with allocating resources to jobs in the most efficient manner possible while keeping cost and time restrictions in mind. Diet Problem: Attempts to determine the most cost-effective combination of meals to suit nutritional needs.
What is an example of linear programming?
A manufacturing business attempting to optimise its production mix in order to maximise revenues is one example of linear programming. The goal is to establish the amounts of various items to create while taking into account resource restrictions such as labour hours, machine availability, and raw resources. The corporation may utilise linear programming to identify the best production quantities by defining a linear objective function and constraints, resulting in greater efficiency and profitability.
Why is it called linear programming?
Because both the goal function and the restrictions are expressed as linear equations or inequalities, it is termed linear programming. The term linear refers to the fact that the coefficients of the variables in the equations are constant (not raised to any power) and that there are no variable interactions or products. Because of this linearity feature, effective mathematical approaches may be used to solve the optimisation issue.
What is two forms of LPP?
The two forms of Linear Programming Problems (LPP) are: Standard Form: Involves maximizing the objective function subject to constraints, where all decision variables are non-negative, and the equations are in the form of ≤. Canonical Form: Requires minimizing the objective function subject to constraints, where decision variables are non-negative, and the equations are in the form of ≥.
Who is the father of linear programming?
George Dantzig is widely regarded as the Father of Linear Programming. Dantzig invented the simplex algorithm, a game-changing approach for tackling linear programming problems, in 1947. His work transformed optimisation approaches, resulting in substantial advances in domains such as operations research, logistics, and economics. Dantzig's innovations have had a significant influence on linear programming and optimisation applications in practise.
What is LPP solution?
The optimal value of the objective function produced by solving a Linear Programming Problem (LPP) is the LPP solution. It is the best possible solution that maximises or minimises the objective function while meeting all of the restrictions.
What is LPP also called?
Linear Programming Optimisation (LPP) is another name for Linear Optimisation.
What are the limitations of LPP?
Linear Programming (LPP) has the following limitations: Linearity Assumption: Linear connections between the goal function and restrictions are required for LPP, which may not correctly describe complicated real-world events. In large-scale situations, the amount of variables and restrictions might become computationally complex. LPP offers continuous solutions, which may not always be viable in discrete decision-making circumstances. Sensitivity to Input Parameters: Minor changes in data might result in drastically different answers, reducing the dependability of outcomes. Infeasibility: Due to competing restrictions or unbounded areas, certain problems may have no possible solutions.
What are the characteristics of LPP?
Linear Programming Problems (LPP) include the following characteristics: Linear equations or inequalities are used to express both the goal function and the limitations. Additivity: The contributions of choice factors in the objective function and restrictions are additive. Proportionality refers to the connection between variables and the objective function. confidence: All of the model's parameters, coefficients, and constants are known with confidence. Decision variables can be continuous or fractional in nature, allowing for partial solutions. Non-negativity: Decision variables must be non-negative (equal to or greater than zero). Optimality: maximising or minimising the objective function while meeting the restrictions. Because of these properties, LPP is suited for a wide range of applications, allowing for efficient optimisation in decision-making processes.





