Dimensions of Tension

Dimensions of Tension

Any physical quantity is measured by comparing it to a basic, arbitrarily chosen, internationally accepted reference standard known as a unit, and a Dimension is a mathematical tool used to study the nature of physical quantities. The basic idea behind dimensions is that we can only add or subtract quantities that have the same dimensions. The dimensional formula, on the other hand, is defined as the expression of a physical quantity in terms of mass, length, and time. In this article, we shall discuss about the dimensions of tension, the dimensional formula of tension and other important information.

Tension is a force that acts along the length of a medium, such as rope or string. To put these objects under tension, a force is required. Tension is also known as an exciting pair, such as an action-reaction pair. [M¹ L¹ T^-2] is the tension dimensional formula. Tension is nothing, but it is a force with a new and improved name. Tension is felt at both ends of the string (from the above picture). Each point on the string has access to the tension force.

Join Our Courses: JEE Class 11 Students | JEE Class 12 Students | JEE Dropper

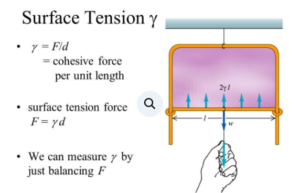
The tension formula on a body is calculated by adding the product of mass and gravitational force, as well as the product of mass and acceleration As a result, the tension equation is T = mg + ma. Surface tension is defined as the phenomenon that occurs when a phase interacts with the surface of a liquid. The other phase could be a liquid as well. Liquids have the smallest surface area. They behave similarly to elastic sheets.

String tension is a non-negative vector quantity. Slack is defined as zero tension. A string or rope is frequently idealised as a one-dimensional object with length but no mass and no cross-section. If there are no bends in the string, as with vibrations or pulleys, tension is a constant along the string, equal to the magnitude of the forces applied by the string’s ends. These are the same forces exerted on the ends of the string by the objects to which the ends are attached, according to Newton’s third law. In the idealised situation where the pulleys are massless and frictionless, the string will still have constant tension along its length if it curves around one or more pulleys.

Dimensional Formula of Tension

The tension dimensional formula is given by,

M¹ L¹ T^-2

Where,

M stands for mass.

T = Time L = Length

Because tension is a type of force, the dimensions of tension equal the dimensions of force.

F = M×a is the formula for force.

The dimensions of,

Mass = [M¹ L⁰ T⁰] . . . . (2)

Acceleration = [M⁰ L¹ T^-2] . . . . (3)

When we substitute equations (2) and (3) into equation (1), we get

M×a = Force

Tension = [M¹ L⁰ T⁰] × [M⁰ L¹ T^-2] = M¹ L¹ T^-2.

M¹ L¹ T^-2 is the dimensional representation of tension.

Make your IIT Dream come true with Infinity Learn.

FAQs

What is the tension unit?

Tension can be a force in physics as a transmitted force, an action-reaction pair of forces, or a restoring force, and its units of force are newtons (or sometimes pounds-force).

Question: Mention some methods that can be used to measure surface tension.

Answer: Here is a list of different surface tension measuring systems:

Method of pendant dropping

Stalagmometric technique

Method of Du Noüy–Padday

Method of spinning drops Method of capillary rise

Method of pendant dropping

Infinity Learn App

Now you can find answers to all your subject queries & prepare for your Exams on our Ultimate Learning App for Classes 6 to 12 – Infinity Learn.