Important Topic of Physics: Electrical potential

Introduction:

Classical mechanics investigates concepts like force, energy, and potential. Force and potential energy are inextricably linked. Any object will accelerate if a net force acts on it. The potential energy of an object decreases as it moves in the direction of the force’s acceleration. The gravitational potential energy of a cannonball present at the top of a hill, for example, is greater than at the bottom of the hill.

As it rolls downhill, its potential energy is converted to motion or kinetic energy. It is also possible to define the potential of certain force fields so that the potential energy of an object in that field is determined solely by the object’s position with respect to the field.

The gravitational field and an electric field are two examples of such force fields (in the absence of time-varying magnetic fields). Because of the intrinsic properties of the object (e.g., mass or charge) and the position of the object, such fields must affect objects.

Objects can have an electric charge, and an electric field exerts a force on charged objects.

If the charged object has a positive charge, the force will be directed in the direction of the electric field vector at that point, whereas a negative charge will cause the force to be directed in the opposite direction. The magnitude of the force can be given as multiplying the quantity of charge by the magnitude of the electric field vector.

An object’s electric potential energy is possessed by virtue of two elements: the charge possessed by the object itself and the relative position of the object with respect to other electrically charged objects. The magnitude of the electric potential is determined by the amount of work done in moving the object from one point to another in the presence of an electric field. When an object moves against an electric field, it gains energy, which is referred to as electric potential energy. The electric potential for any charge is calculated by dividing the potential energy by the quantity of charge.

Overview:

The amount of work required to move a unit charge from a reference point to a specific point against an electric field is referred to as electric potential. The reference point is usually Earth, but any place outside the electric field charge’s effect might be utilized.

A positive charge’s potential energy increases when it moves against an electric field and decreases when it moves with the electric field; a negative charge’s potential energy decreases when it moves with the electric field. Unless the unit charge passes through a changing magnetic field, its potential at any given point is independent of the path taken.

Although the concept of electric potential is useful for understanding electrical phenomena, only potential energy differences are measurable. An electric potential can be thought of as the potential energy per unit charge if an electric field is defined as the force per unit charge.

As a result, the work required to move a unit charge from one point to another (for example, within an electric circuit) is equal to the difference in potential energies at each point. The International System of Units (SI) expresses electric potential in joules per coulomb (volts), and potential energy differences are measured with a voltmeter.

Electric Potential :

Electricity is the passage of electric charges that is responsible for producing electric current. Electricity has become increasingly crucial for humans in our fast-paced era. Everything from a modest room fan to massive factory machines runs on electricity. Electric Potential is a key term in the field of electricity. To produce electricity, a potential difference is required to create the flow of electrons.

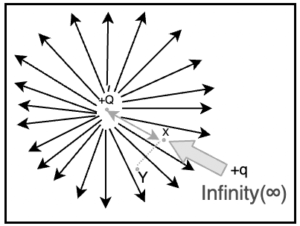
It is the amount of labour done per unit charge to get that charge from infinity to a point in the electrostatic field while resisting the field force. Voltage is another term for electric potential. Voltage or Volts is the SI unit for Electric Potential or Electric Potential Difference. A scalar quantity is an electric potential.

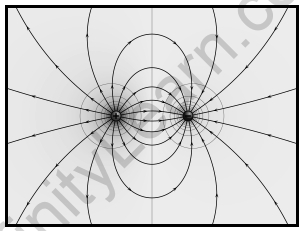
Electric Potential Due to Multiple Charges

The potential energy of a system with three charges q1, q2, and q3 at the vertices of a triangle is,

U=U _{1 2}+U₂₃+U₃₁

=1/4πε₀q₁q₂/d₁+q₂q₃/d₂+q₃q₁/d₃

If four charges, q1, q2, q3, and q4, are placed at the four corners of a square, the electric potential energy of the system is,

U=1/4πε₀q₁q₂/d+q₂q₃/d+q₃q₄/d+q₄q₁/d+q₄q₂/2d+q₃q₁/2d

Special Case: In the field of a charge Q, the work done is given by, if a charge q is transferred against the electric field from a distance ‘a’ to a distance ‘b’ from Q.

W=Vb-Va×q

=1/4πε₀×(Qq/b)-1/40×(Qq/a)=Qq/40[1/b-1/a]=Qq/40[(a-b)/ab]

Electric potential energy:

The electric potential energy of any given charge or system of charges is defined as the total work done by an external agent in bringing the charge or system of charges from infinity to the current configuration without acceleration. Electric potential energy is defined as the total potential energy that a unit charge will have if it is located at any point in outer space.

The entire work done by an external agent in moving a charge or system of charges from infinity to the current configuration without acceleration is defined as the electric potential energy of that charge or system of charges.

The entire potential energy that a unit charge will have if it is positioned everywhere in space is known as electric potential energy.

Crack NEET with Result-Oriented Learning Program from Infinity Learn

Frequently Asked Question (FAQs):

Question: What is the difference in electric potential?

Answer: The potential between two points (E) in an electrical circuit is defined as the amount of work (W) done by an external agent in transporting a unit charge (Q) from one point to another.

On a mathematical level, we can state,

W/Q = E

Question: What is Electric Potential Energy, and how does it work?

Answer: The entire potential energy a unit charge will have if it is positioned everywhere in space is known as electric potential energy.

Infinity Learn App

Now you can find answers to all your subject queries & prepare for your Exams on our Ultimate Learning App for CBSE and K-12 – Infinity Learn.