Table of Contents
The dimensionless Reynolds number is important in predicting patterns in fluid behavior. The Reynolds number, abbreviated as Re, determines whether the fluid flow is laminar or turbulent. It is one of the most important controlling parameters in all viscous flows in which a numerical model is chosen based on a pre-calculated Reynolds number. Although the Reynolds number includes both static and kinetic fluid properties, it is specified as a flow property because dynamic conditions are studied. In physics, the Reynolds number is the ratio of inertial forces to viscous forces. This ratio distinguishes laminar flows from turbulent flows.
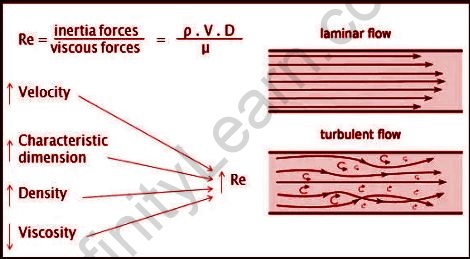
The Reynolds number is a useful parameter for predicting whether a flow condition will be laminar or turbulent because it represents the ratio of inertial forces to viscous forces. It is calculated by multiplying a characteristic length by a characteristic velocity and dividing the result by the kinematic viscosity. When viscous forces are dominant (low Re, slow flow), they are enough to maintain all of the fluid particles in line, resulting in a laminar flow. Even very low Re indicates viscous creeping motion with negligible inertia effects. Turbulent flow occurs when inertial forces dominate viscous forces (when the fluid flows faster and Re is greater). The transition from laminar to turbulent flow is influenced by factors such as surface geometry, surface roughness, free-stream velocity, surface temperature, and fluid type, among others.
Osborn Reynolds discovered that the flow regime in a fluid is primarily determined by the ratio of inertia forces to viscous forces. When viscous forces are dominant (low Re, slow flow), they are sufficient to keep all fluid particles in line, and the flow is laminar. Turbulent flow occurs when inertial forces dominate viscous forces (when the fluid flows faster and Re is greater). The formula for the Reynolds number determines whether the fluid will be turbulent or laminar. If the fluid flow has a Reynolds number greater than 4,000, it is considered turbulent. Reynolds number is unitless and is represented by the symbol Re. The Reynolds number is one of the most important controlling parameters in any viscous flow in which a numerical model is chosen based on a pre-calculated Reynolds number.
Overview:
The Reynolds number’s applicability varies based on the fluid flow’s characteristics, such as density variation (compressibility), viscosity variation (Non-Newtonian), internal or external flow, and so on. The crucial Reynolds number is an expression of the value used to define the transition between regimes, which varies depending on the flow type and shape. The critical Reynolds number for turbulent flow in a pipe is 2000, but the critical Reynolds number for turbulent flow over a flat plate, when the flow velocity is the free-stream velocity, is in the range of 1000 to 2000.
If the fluids are Newtonian, the Reynolds number also predicts the viscous behaviour of the flow. As a result, it’s critical to understand the physical situation in order to prevent making incorrect forecasts. Internal and external flows, as well as transition regimes, are the primary subjects of study for the Reynolds number. Fluids with a constant viscosity are known as Newtonian fluids. It makes no difference how much stress is applied to a Newtonian fluid if the temperature remains constant; it will always have the same viscosity. Water, alcohol, and mineral oil are just a few examples.
Reynolds Number Formula:
It is given by the following relation:
Reynolds Number = Inertial Force / Viscous Force
Re=ρVD / µ
Where,
Reynolds’ number is Re
ρ = the fluid’s density (in kilogrammes per cubic metre).
The flow velocity is denoted by the letter V.
The pipe diameter is D, and the fluid viscosity is µ .
If the calculated Reynolds number is high (greater than 2000), the flow through the pipe is said to be turbulent. These are numerically acceptable values, but in general, laminar and turbulent flows are classified according to a range. Laminar flow has a Reynolds number less than 1100, while turbulent flow has a number greater than 2200. Laminar flow is a type of flow in which the fluid moves smoothly and in predictable paths. Turbulent flow, on the other hand, is not smooth and follows irregular math with a lot of mixing.
The Reynolds number is named after Osborne Reynolds, a British physicist. He discovered this while studying fluid flow characteristics such as the flow of a liquid through a pipe and the motion of an aeroplane wing through the air. He also noticed that the flow type can abruptly change from laminar to turbulent.
Reynolds number units:
The gas molecules in the atmosphere near an object are disturbed and move around it as it moves through the atmosphere. Between the gas and the object, aerodynamic forces are generated. The magnitude of these forces is determined by the shape of the object, its speed, the mass of the gas passing through it, and two other important properties of the gas: viscosity, or stickiness, and compressibility, or springiness. Aerodynamicists use similarity parameters, which are ratios of these effects to other forces in the problem, to properly model these effects. If the similarity parameters in two experiments are the same, then the relative importance of the forces is correctly modeled. On another page, representative values for air properties are given, but the actual value of the parameter depends on the state of the gas and the altitude.
The Reynolds number has no dimensions. High values of the parameter (on the order of ten million) indicate that viscous forces are low and the flow is essentially inviscid. The flow can then be modeled using the Euler equations. Low parameter values (on the order of one hundred) indicate that viscous forces must be considered.
Reynolds number value:
If the value of Nr is between 0 and 2000, the liquid flow is streamlined or laminar. The flow is turbulent above 4000, and the flow of the liquid is unstable between 2000 and 3000, i.e., changing between the laminar and turbulent flow.
| Sr. No | Item | Typical Reynolds Number |
| 1 | Laminar Flow | <2100 |
| 2 | Turbulent Flow | >4000 |
| 3 | Person Swimming | 4×106 |
| 4 | Blue Whale | 4×108 |
| 5 | Smallest fish | 1 |
| 6 | Atmospheric tropical cyclone | 1×1012 |
| 7 | Bacterium | 1×10-4 |
| 8 | Blood flow in brain | 1×102 |
| 9 | Blood flow in aorta | 1×103 |
| 10 | Fastest fish | 1×108 |
Laminar flow is defined as the smooth flow of layers. It is usually little or no mixing and the fluid velocity is lower. The fluid particle motion is ordered, with no cross currents. This is most common in fluids with high viscosity and at low speeds. For laminar flow, Reynold’s Number is less than 2100.
There is turbulence and unpredictable mixing in a turbulent flow. The velocity is high, and the fluids do not move in layers as they do in laminar flow. Storms, waves in the sea or river, and so on are examples of typical turbulent flow. The Reynolds Number for turbulent flow is typically greater than 4000.
The inertial effect becomes negligible at low Reynolds Number Re. The flow behaviour is viscosity-dependent, and the flow is stable. When the Reynolds Number Re is extremely high, however, the viscous effects are negligible. The fluid flow behavior is determined by the fluid’s momentum, and the flow is unsteady.
Also read: NEET Exam Pattern 2022
Frequently Asked Questions
What does Reynolds Number Mean?
The number of revolutions (Nr) of a liquid flowing through a pipe is defined as the product of density times velocity times length divided by the coefficient of viscosity. The ratio of inertial forces and viscous forces per unit area in a fluid flow determines the value of Nr.
At what Reynolds number is turbulent flow?
If the Reynolds number for external flow is greater than 3500, the flow is turbulent.
What is the critical Reynolds number?
The critical Reynolds number is associated with the laminar-turbulent transition, which occurs when a laminar flow transforms into a turbulent flow. This is an extremely complicated process that is still not fully understood.







