Area of a Pentagon Formula

Introduction:

A pentagon is a two-dimensional geometrical figure with five sides. Its area refers to the region enclosed by these sides. The term “pentagon” is derived from the Greek words ‘Penta’ meaning ‘five’ and ‘gon’ meaning ‘angles’. In this lesson, we will explore various aspects of finding the area of a pentagon, including the area formula for both regular and irregular pentagons

Area of Pentagon Formula:

1. Area of Regular Pentagon: In a regular pentagon, all sides and angles are equal.

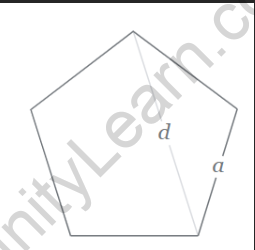
The area of a pentagon can be calculated using different formulas depending on the given information. One common formula for finding the area of a regular pentagon is:

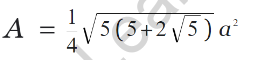
In this formula, ‘a’ represents the length of the side of the regular pentagon. By substituting the value of ‘a’ into the formula, we can easily calculate the area.

2. Area of Pentagon using Apothem:

The apothem of a polygon is defined as the distance from the center of the polygon to the midpoint of any of its sides. In the case of a regular polygon, such as a regular pentagon, the apothem is a line segment that is perpendicular to any of the sides and reaches the center of the polygon. The apothem divides the polygon into congruent triangles, and it is useful in calculating the area of the polygon using the formula:

Area of pentagon = 1/2 × p × a

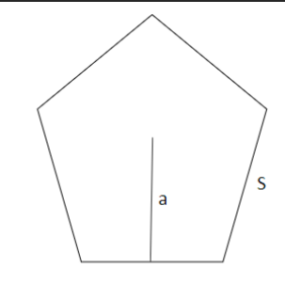
Here, ‘p’ is the perimeter and ‘a’ is the apothem of the pentagon. Observe the following pentagon to see the apothem ‘a’ and the side length ‘s’.

3. Area of irregular pentagon:
If the pentagon is irregular, and its side lengths are not equal, calculating the area becomes more complex. In such cases, we can use a different approach called the triangulation method. The pentagon is divided into triangles, and the area of each triangle is calculated separately. The sum of the areas of all the triangles gives the total area of the pentagon.

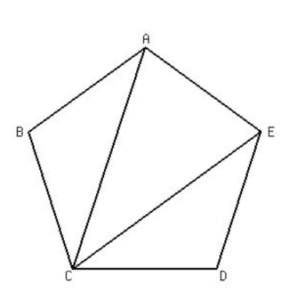
For example, if we have an irregular pentagon with vertices A, B, C, D, and E, we can divide it into three triangles: ABC, ACD, and ADE. We can then calculate the area of each triangle using the formula for the area of a triangle, which is (1/2) × base × height. The sum of the areas of these three triangles will give us the total area of the pentagon.

It’s important to note that the accuracy of the area calculation depends on the precision of the measurements and the assumed shape of the pentagon. The formulas mentioned above assume that the pentagon is planar and has no thickness.

Applications of Area of Pentagon Formula:

In real-world applications, the area of a pentagon is often calculated using computer software or mathematical techniques such as integration. These methods can provide more precise results, especially for irregular or complex pentagons.

Understanding the formulas and methods for calculating the area of a pentagon allows us to determine the size and spatial characteristics of this geometric shape, enabling us to solve various mathematical and practical problems.

Solved Examples on Area of a Pentagon Formula:

Example 1: Find the area of a regular pentagon with a side length of 8 units.

Solution:

To find the area of a regular pentagon, we can use the formula:

Area = (1/4) × s² × √(5(5 + 2√5))

Plugging in the given side length:

Area = (1/4) × (8)² × √(5(5 + 2√5))

= (1/4) × 64 × √(5(5 + 2√5))

= 16 × √(5(5 + 2√5))

≈ 110.78 square units (rounded to two decimal places)

Therefore, the area of the regular pentagon is approximately 110.78 square units.

Example 2: Determine the area of an irregular pentagon with the following side lengths: 5 units, 7 units, 6 units, 8 units, and 9 units.

Solution:

To find the area of an irregular pentagon, we can divide it into triangles and calculate their areas separately.

Divide the pentagon into three triangles: ABC, CDE, and EAB.

Triangle ABC: Base = AB = 5 units, Height = h₁ (to be determined)

Triangle CDE: Base = CD = 6 units, Height = h₂ (to be determined)

Triangle EAB: Base = EA = 9 units, Height = h₃ (to be determined)

Calculate the areas of each triangle:

Area(ABC) = (1/2) × AB × h₁

Area(CDE) = (1/2) × CD × h₂

Area(EAB) = (1/2) × EA × h₃

Once we determine the heights of each triangle, we can calculate their respective areas using the formula for the area of a triangle.

Example 3: Find the area of a pentagon with an apothem of length 8 units and a side length of 10 units.

Solution:

Step 1: Calculate the perimeter of the pentagon.

Since a regular pentagon has five equal sides, the perimeter is simply 5 times the side length.

Perimeter = 5 × 10 = 50 units.

Step 2: Find the area using the apothem and perimeter.

The area of a regular pentagon can be calculated using the formula: Area = (apothem × perimeter) / 2.

In this case, the apothem is 8 units and the perimeter is 50 units.

Area = (8 × 50) / 2

= 400 / 2

= 200 square units.

Therefore, the area of the pentagon is 200 square units.

Frequently Asked Questions on Area of a Pentagon Formula:

1: What is the perimeter and area of regular pentagon?
Answer: The perimeter of a regular pentagon is equal to 5 times the length of its side. The area of a regular pentagon can be calculated using the formula: Area = (1/4) × √(5 × (5 + 2√5)) × side length².

2: What is the pentagon angle formula?

Answer: The pentagon angle formula states that the sum of the interior angles of a pentagon is equal to 540 degrees. In a regular pentagon, each interior angle measures 108 degrees.

3: What is apothem in polygon?

Answer: In a polygon, the apothem is the distance from the center of the polygon to the midpoint of any of its sides. It is a line segment that is perpendicular to the side it intersects. The apothem is used to calculate the area of a polygon by dividing it into congruent triangles.

4: How to find the area of irregular pentagon?

Answer: To find the area of an irregular pentagon, you can divide it into smaller, familiar shapes (triangles, rectangles, etc.) and calculate the area of each individual shape. Add up the areas of these smaller shapes to find the total area of the pentagon. Alternatively, you can use the shoelace formula, which involves determining the coordinates of the vertices of the pentagon and using them to calculate the area.

5: Is any 5-sided shape a pentagon?

Answer: No, not every 5-sided shape is considered a pentagon. To be classified as a pentagon, a 5-sided shape must meet certain criteria. It must have five straight sides that do not intersect, and its interior angles must sum up to 540 degrees.

6: What is the difference between regular and irregular pentagon?

Answer: The main difference between a regular and irregular pentagon lies in their properties. A regular pentagon has all sides and angles equal, while an irregular pentagon has different side lengths and varying angle measures. Regular pentagons have symmetry and can be inscribed in a circle, whereas irregular pentagons lack these characteristics.

7: How to find the Area of Pentagon with Apothem?

Answer: To find the area of a pentagon with an apothem, multiply the apothem length by half the perimeter of the pentagon. The perimeter is obtained by multiplying the length of one side by five. Finally, divide the result by 2 to get the area of the pentagon.

8: How to find the Area of Pentagon with Side Length?

Answer: To find the area of a pentagon with a known side length, divide the pentagon into five congruent triangles by drawing lines from the center to each vertex. Calculate the area of one of these triangles using the formula (1/2) x base x height. Multiply this area by 5 to account for all five triangles and obtain the total area of the pentagon.