Table of Contents
Introduction:
Surface area refers to the total area that covers the outer surface of a three-dimensional object. It includes the sum of all the areas of the object’s individual faces or surfaces. Surface area is typically measured in square units, such as square centimeters or square meters. It is an important concept in geometry and is used to determine the amount of material required to cover or wrap an object, as well as in various calculations and formulas related to shapes and structures.
What is a Sphere?

A sphere is a 3-dimensional shape that is round and has no vertices.
- In the above sphere, O is the centre of the sphere.
- All the points on the surface of the sphere are equidistant from its centre.
- This distance is the radius of the sphere.
- If a semicircle is revolved 360° around its diameter, we get a sphere.
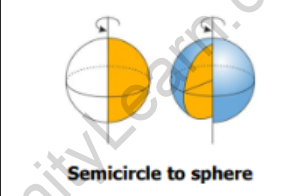
What is the Surface area of a sphere?
A sphere has just one type of surface area.
The total surface area of the sphere is its curved surface area as it does not have any flat
surfaces.
Surface area of a sphere = 4πr2
What is a Hemisphere?
If a sphere is cut in half, it will lead to two hemispheres. Thus, a hemisphere is half a sphere. Its radius is the same as the radius of the sphere.
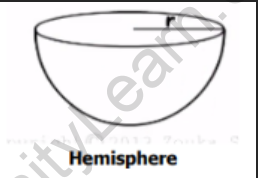
What is the Surface area of a hemisphere?
A hemisphere has a flat surface and a curved surface.
- Curved surface area of a hemisphere:
This is half of the surface area of the sphere
Curved surface area of hemisphere = 2πr2
- Total surface area of a hemisphere:
Total surface area of hemisphere = Area(Curved surface) + Area(Circle on top)
∴ Total surface area of hemisphere = 2πr2 + πr2
∴ Total surface area of hemisphere = 3πr2
Solved Examples on Surface Area of Sphere Formula:
Example 1: Find the surface area of a sphere with a radius of 3.5 units.
Solution:
Given: Radius (r) = 3.5 units
Surface Area = 4πr²
Surface Area = 4 x 3.14159 x 3.52
Surface Area ≈ 4 x 3.14159 x 12.25
Surface Area ≈ 153.938 square units
Therefore, the surface area of the sphere with a radius of 3.5 units is approximately 153.938 square units.
Example 2: A water tank in the shape of a hemisphere has a radius of 5 meters. Find the total surface area of the tank.
Solution:
Given: Radius (r) = 5 meters
Step 1: Calculate the surface area of the hemisphere
Surface Area = 2πr²
Surface Area = 2 x 3.14159 x 52
Surface Area = 2 x 3.14159 x 25
Surface Area ≈ 157.0795 square meters
Step 2: Calculate the surface area of the flat circular base
Base Area = πr²
Base Area = 3.14159 x 52
Base Area = 3.14159 x 25
Base Area ≈ 78.5398 square meters
Step 3: Calculate the total surface area of the hemisphere (including the base)
Total Surface Area = Surface Area + Base Area
Total Surface Area ≈ 157.0795 + 78.5398
Total Surface Area ≈ 235.6193 square meters
Frequently Asked Questions on Surface Area of Sphere Formula:
1: What is the TSA and CSA of a sphere?
Answer: The TSA (Total Surface Area) and CSA (Curved Surface Area) of a sphere are the same. They represent the sum of the surface areas of the curved portion of the sphere. The formulas for both the TSA and CSA of a sphere are given by 4πr², where “r” is the radius of the sphere. Since a sphere has no flat faces, the TSA and CSA refer to the entire outer surface area, including both the curved surface and the areas of the top and bottom hemispherical caps.
2: How is the surface area of a sphere different from the volume of a sphere?
Answer: The formula for the surface area of a sphere, 4πr², measures the total area covered by the outer surface of the sphere. It quantifies the amount of surface material on the sphere. On the other hand, the formula for the volume of a sphere, (4/3)πr³, calculates the amount of space enclosed within the sphere. It represents the three-dimensional capacity or the amount of substance the sphere can hold. While both formulas involve the radius (r) and utilize π, they measure different aspects of a sphere – surface area for the outer covering and volume for the internal space.
3: What is the LSA of sphere?
Answer: The term “LSA” typically does not refer to a recognized measurement or property of a sphere. In the context of a sphere, the commonly used terms are “TSA” (Total Surface Area) and “CSA” (Curved Surface Area). The total surface area of a sphere refers to the sum of all the surface areas, including both the curved surface and the areas of the top and bottom hemispherical caps. The TSA (Total Surface Area) and CSA (Curved Surface Area) of a sphere are the same.
4: What is the CSA and TSA of a hemisphere?
Answer: In the case of a hemisphere, the CSA (Curved Surface Area) refers specifically to the surface area of the curved portion of the hemisphere. The formula to calculate the CSA of a hemisphere is 2πr², where “r” represents the radius of the hemisphere. On the other hand, the TSA (Total Surface Area) of a hemisphere encompasses the entire surface area, including both the curved surface area and the area of the flat circular base. The formula for the TSA of a hemisphere is derived by adding the CSA and the base area, resulting in TSA = 2πr² + πr², which simplifies to TSA = 3πr².
5: What is the surface area of sphere?
Answer: The surface area of a sphere is given by the formula 4πr², where “r” represents the radius of the sphere. The formula calculates the total area covered by the outer surface of the sphere. The term “4” in the formula accounts for the fact that a sphere has a symmetrical shape, and “πr²” represents the surface area of a single circular face of the sphere. The surface area of a sphere is the same in all directions, as the sphere lacks edges or corners. This formula is widely used in various fields, such as mathematics, physics, engineering, and geometry, to calculate the surface area of spherical objects or solve related problems.
6: How to find the surface area of sphere?
Answer: To find the surface area of a sphere, you can use the formula:
A = 4πr²
where A represents the surface area and r is the radius of the sphere.
Here are the steps to calculate the surface area of a sphere:
- Determine the radius (r) of the sphere.
- Square the radius by multiplying it by itself (r²).
- Multiply the squared radius by 4.
- Multiply the result by π (pi) to get the surface area.
For example, if the radius of the sphere is 5 units, the calculation would be:
A = 4π(5²) = 4π(25) = 100π square units
So, the surface area of the sphere is 100π square units.
7: What is the surface area formula for sphere?
Answer: The surface area (A) of a sphere can be calculated using the formula:
A = 4πr²
where A represents the surface area and r is the radius of the sphere.
8: Does a Sphere have Infinite Faces?
Answer: No, a sphere does not have any faces. Unlike flat surfaces found in other geometric shapes, a sphere is entirely curved, without any flat regions. This unique characteristic renders the sphere a faceless three-dimensional object.
9: How does the surface area of sphere change when the radius is halved?
Answer: When the radius of a sphere is halved, the surface area is reduced by a factor of four. The surface area of a sphere is directly proportional to the square of its radius. Therefore, if the radius is halved, the new surface area will be one-fourth (1/4) of the original surface area. This relationship demonstrates that reducing the radius has a significant impact on the surface area of a sphere.









