Table of Contents
Class 7 Maths Chapter 6 Exercise 6.5 Solution – Triangle and Its Properties
The NCERT solutions for Class 7 Maths Chapter 6 Exercise 6.5, get into the fundamentals of triangles, encompassing Pythagoras’ theorem and the angle sum property. These NCERT solutions, aligned with the CBSE syllabus and NCERT textbook, provide essential insights:
- Pythagoras’ theorem elucidates that in a right-angled triangle, the square of the hypotenuse (the longest side) equals the sum of the squares of the other two sides.
- The converse of Pythagoras’ theorem, a critical aspect covered in NCERT solutions for Class 7 Maths Chapter 6, aids in determining whether a given triangle is right-angled. If the lengths of the sides (a, b, and c) satisfy the equation a² + b² = c², the triangle qualifies as right-angled.
- Pythagorean triplets, highlighted in NCERT solutions for Class 7 Maths Chapter 6, are trios of positive integers (a, b, and c) satisfying the equation c² = a² + b². Examples, like (3, 4, 5), (5, 12, 13), and (8, 15, 17), illustrate this concept.
- The angle sum property, another pivotal concept addressed in NCERT solutions for Class 7 Maths Chapter 6, asserts that the total sum of angles in any triangle invariably amounts to 180 degrees. This property serves as a cornerstone for resolving diverse triangle-related problems.
- Additionally, these NCERT solutions for class 7 gets into various other triangle properties, elucidating the interplay between sides and angles and providing methodologies for determining unknown angles or sides based on given information.
By thoroughly grasping the concepts delineated in these NCERT solutions for Class 7 Maths Chapter 6, students can construct a robust foundation in geometry, equipping themselves to tackle a plethora of triangle-related problems with confidence.
Also Check:
NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5 Updated for 2024-25
Here are the solutions for Class 7 Maths chapter 6 exercise 6.5 questions
1. PQR is a triangle, right angled at P. If PQ = 10 cm and PR = 24 cm, find QR.
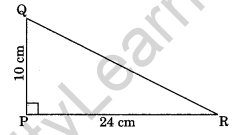
Solution:
In right angled triangle PQR, we have
QR2 = PQ2 + PR2 From Pythagoras property)
= (10)2 + (24)2
= 100 + 576 = 676
∴ QR = \(\sqrt{676}\) = 26 cm
The, the required length of QR = 26 cm.
2. ABC is a triangle, right-angled at C. If AB = 25 cm and AC = 7 cm, find BC.
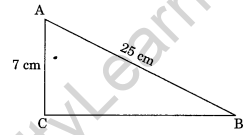
Solution:
In right angled∆ABC, we have
BC2 + (7)2 = (25)2 (By Pythagoras property)
⇒ BC2 + 49 = 625
⇒ BC2 = 625 – 49
⇒ BC2 = 576
∴ BC = \(\sqrt{576}\) = 24 cm
Thus, the required length of BC = 24 cm.
3. A 15 m long ladder reached a window 12 m high from the ground on placing it against a wall at a distance a. Find the distance of the foot of the ladder from the wall.
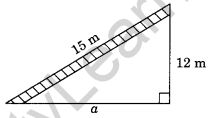
Solution:
Here, the ladder forms a right angled triangle.
∴ a2 + (12)2 = (15)2 (By Pythagoras property)
⇒ a2+ 144 = 225
⇒ a2 = 225 – 144
⇒ a2 = 81
∴ a = \(\sqrt{81}\) = 9 m
Thus, the distance of the foot from the ladder = 9m
4. Which of the following can be the sides of a right triangle?
- 2.5 cm, 6.5 cm, 6 cm.
- 2 cm, 2 cm, 5 cm.
- 1.5 cm, 2 cm, 2.5 cm
Solution:
(i) Given sides are 2.5 cm, 6.5 cm, 6 cm.
Square of the longer side = (6.5)2 = 42.25 cm.
Sum of the square of other two sides
= (2.5)2 + (6)2 = 6.25 + 36
= 42.25 cm.
Since, the square of the longer side in a triangle is equal to the sum of the squares of other two sides.
∴ The given sides form a right triangle.
(ii) Given sides are 2 cm, 2 cm, 5 cm .
Square of the longer side = (5)2 = 25 cm Sum of the square of other two sides
= (2)2 + (2)2 =4 + 4 = 8 cm
Since 25 cm ≠ 8 cm
∴ The given sides do not form a right triangle.
(iii) Given sides are 1.5 cm, 2 cm, 2.5 cm
Square of the longer side = (2.5)2 = 6.25 cm Sum of the square of other two sides
= (1.5)2 + (2)2 = 2.25 + 4
Since 6.25 cm = 6.25 cm = 6.25 cm
Since the square of longer side in a triangle is equal to the sum of square of other two sides.
∴ The given sides form a right triangle.
5. A tree is broken at a height of 5 m from the ground and its top touches the ground at a distance of 12 m from the base of the tree. Find the original height of the tree.
Solution:
Let AB be the original height of the tree and broken at C touching the ground at D such that
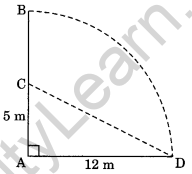
AC = 5 m
and AD = 12 m
In right triangle ∆CAD,
AD2 + AC2 = CD2 (By Pythagoras property)
⇒ (12)2 + (5)2 = CD2
⇒ 144 + 25 = CD2
⇒ 169 = CD2
∴ CD = \(\sqrt{169}\) = 13 m
But CD = BC
AC + CB = AB
5 m + 13 m = AB
∴ AB = 18 m .
Thus, the original height of the tree = 18 m.
6. Angles Q and R of a ΔPQR are 25o and 65o.
Write which of the following is true:
- PQ2 + QR2 = RP2
- PQ2 + RP2 = QR2
- RP2 + QR2 = PQ2
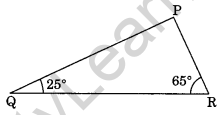
Solution:
We know that
∠P + ∠Q + ∠R = 180° (Angle sum property)
∠P + 25° + 65° = 180°
∠P + 90° = 180°
∠P = 180° – 90° – 90°
∆PQR is a right triangle, right angled at P
(i) Not True
∴ PQ2 + QR2 ≠ RP2 (By Pythagoras property)
(ii) True
∴ PQ2 + RP2 = QP2 (By Pythagoras property)
(iii) Not True
∴ RP2 + QR2 ≠ PQ2 (By Pythagoras property)
7. Find the perimeter of the rectangle whose length is 40 cm and a diagonal is 41 cm.
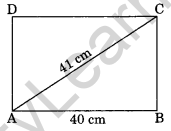
Solution:
Given: Length AB = 40 cm
Diagonal AC = 41 cm
In right triangle ABC, we have
AB2 + BC2= AC2 (By Pythagoras property)
⇒ (40)2 + BC2 = (41)2
⇒ 1600 + BC2 = 1681
⇒ BC2 = 1681 – 1600
⇒ BC2 = 81
∴ BC = \(\sqrt{81}\) = 9 cm
∴ AB = DC = 40 cm and BC = AD = 9 cm (Property of rectangle)
∴ The required perimeter
= AB + BC + CD + DA
= (40 + 9 + 40 + 9) cm
= 98 cm
8. The diagonals of a rhombus measure 16 cm and 30 cm. Find its perimeter.

Solution:
Let ABCD be a rhombus whose diagonals intersect each other at O such that AC = 16 cm and BD = 30 cm
Since, the diagonals of a rhombus bisect each other at 90°.
∴ OA = OC = 8 cm and OB = OD = 15 cm
In right ∆OAB,
AB2 = OA2 + OB2 (By Pythagoras property)
= (8)2+ (15)2 = 64 + 225
= 289
∴ AB =\(\sqrt{289}\)= 17 cm
Since AB = BC = CD = DA (Property of rhombus)
∴ Required perimeter of rhombus
= 4 × side = 4 × 17 = 68 cm.
- Chapter 1 Integers
- Chapter 2 Fractions and Decimals
- Chapter 3 Data Handling
- Chapter 4 Simple Equations
- Chapter 5 Lines and Angles
- Chapter 6 The Triangles and Its Properties
- Chapter 7 Congruence of Triangles
- Chapter 8 Comparing Quantities
- Chapter 9 Rational Numbers
- Chapter 10 Practical Geometry
- Chapter 11 Perimeter and Area
- Chapter 12 Algebraic Expressions
- Chapter 13 Exponents and Powers
- Chapter 14 Symmetry
- Chapter 15 Visualizing Solid Shapes
NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5 PDF Download
Download the NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5 in PDF format to ensure comprehensive preparation and a deeper understanding of the concepts. These expertly crafted solutions help students tackle various mathematical problems with ease, enhancing their ability to score higher in exams. Click here to access and download the PDF now for detailed, step-by-step solutions that support your study efforts efficiently. Get your free copy today and excel in your Maths exams.
| Other Resources for Class 7 | |
| NCERT Exemplar Solutions Class 7 | NCERT Books for Class 7 |
| Class 7 Worksheets | NCERT Solutions for Class 7 |
FAQs on NCERT Solutions for Class 7 Maths Chapter 6 Exercise 6.5
What is Pythagoras' theorem in Chapter 6 The Triangle and its Properties of Exercise 6.5 in NCERT Class 7 Maths?
In Chapter 6, The Triangle and its Properties, of Exercise 6.5 in NCERT Class 7 Maths, Pythagoras' theorem is described as stating that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides.
How will the final exams benefit from using the NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties (Exercise 6.5)?
Using the NCERT Solutions for Class 7 Maths Chapter 6, The Triangle and its Properties (Exercise 6.5), offers several benefits for final exam preparation. These solutions provide clearly solved examples and step-by-step methods to solve problems, enhancing students' understanding of key concepts and equipping them with strategies to tackle complex questions in the final exams.
What is a Rhombus in Class 7 Maths Chapter 6 The Triangle and its Properties?
In Class 7 Maths, Chapter 6 The Triangle and its Properties, a rhombus is defined as a type of parallelogram characterized by four sides of equal length, opposite sides that are parallel, and opposite angles that are equal. Additionally, the diagonals of a rhombus bisect each other at right angles.
What is a Rectangle in Class 7 Maths Chapter 6 The Triangle and its Properties?
A rectangle, as described in Class 7 Maths, Chapter 6 The Triangle and its Properties, is a type of quadrilateral with four right angles, making it a parallelogram where each angle is a right angle and all angles are equal. A special case of a rectangle is a square, where all four sides are of equal length.
Where can I find the most up-to-date NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties (Exercise 6.5)?
The latest NCERT Solutions for Class 7 Maths Chapter 6 The Triangle and its Properties (Exercise 6.5) can be found on Infinity Learn, India’s premier e-learning platform. These solutions are meticulously crafted by subject experts at Infinity Learn, adhering to CBSE guidelines, ensuring clarity and precision in the material.







