Table of Contents
NCERT Solutions for Class 11 Geography Chapter 4 Map Projections are available below and in PDF for free download. These NCERT solutions are prepared according to the latest syllabus, NCERT books, and exam pattern suggested by CBSE, NCERT, and KVS. Questions from the NCERT book are crucial for exams and can help you score higher if answered correctly. For more chapter-wise solutions for NCERT Class 11 Geography and other subjects, download our latest study material. Chapter 4, Map Projections, is an important topic in Class 11; refer to the answers below to improve your exam performance.
Chapter 4 Map Projections Class 11 Geography NCERT Solutions
Class 11 Geography students can benefit from the NCERT questions and answers provided for Chapter 4 on Map Projections. These solutions are essential for exam preparation and can lead to scoring well in the subject.
Chapter 4 Map Projections NCERT Solutions Class 11 Geography
1. Choose the right answer from the four alternatives given below:
Question (i). A map projection least suitable for the world map:
(а) Mercator
(b) Simple Cylindrical
(c) Conical
(d) All the above
Answer: (c) Conical
Question (ii). A map projection that is neither the equal-area nor the correct shape and even the directions are also incorrect
(a) Simple Conical
(b) Polar zenithal
(c) Mercator
(d) Cylindrical
Answer: (a) Simple Conical
Question (iii). A map projection having correct direction and correct shape but area greatly exaggerated.polewards is:
(a) Cylindrical Equal Area
(b) Mercator
(c) Conical
(d) All the above
Answer: (b) Mercator
Question (iv). When the source of light is placed at the centre of the globe, the resultant projection is called:
(a) Orthographic
(b) Stereographic
(c) Gnomonic
(d) All the above
Answer:(c) Gnomonic
Answer the following questions in about 30 words:
Question (i). Describe the elements of map projection.
Answer:
- Reduced Earth: A model of the earth is represented by the help of a reduced scale on a flat sheet of paper. This model is called the “reduced earth”.
- Parallels of Latitude: These are the circles running round the globe parallel to the equator and maintaining uniform distance from the poles.
- Meridians of Longitude: These are semi-circles drawn in north-south direction from one pole to the other, and the two opposite meridians make a complete circle, i.e. circumference of the globe.
- Global Property: In preparing a map projection the following basic properties of the global surface are to be preserved by using one or the other methods:
- Distance between any given points of a region;
- Shape of the region;
- Size or area of the region in accuracy;
- Direction of any one point of the region bearing to another point.
Question (ii). What do you mean by global property?
Answer: In preparing a map projection the following basic properties of the global surface are to be preserved by using one or the other methods:
- Distance between any given points of a region;
- Shape of the region;
- Size or area of the region in accuracy;
- Direction of any one point of the region bearing to another point.
Question (iii).Not a single map projection represents the globe truly. Why?
Answer: However, there is no such projection, which maintains the scale correctly throughout. It can be maintained correctly only along some selected parallels and meridians as per the requirement. Projection is a shadow of globe which has to be presented on a map. When shape of globe changes certainly inaccuracy comes in. Therefore, it is rightly said that not a single map projection represents the globe truly.
Question (iv). How is the area kept equal in cylindrical equal area projection?
Answer: The area is kept equal in cylindrical equal area projection because latitudes and longitudes intersect each other at right angles in the straight line form.
3. Differentiate between:
Question (i). Developable and non-developable surfaces
Answer:
| Basis | Developable Surface | Non-developable Surface |
| Meaning | A developable surface is one, which can be flattened, and on which, a network of latitude and longitude can be projected. | A non-developable surface is one, which cannot be flattened without shrinking, breaking or creasing. |
| Example | A cylinder, a cone and a plane have the property of developable surface. | A globe or spherical surface has the property of non-developable surface |
On the basis of nature of developable surface, the projections are classified as cylindrical, conical and zenithal projections.
Question (ii). Homolographic and orthographic projections
Answer:
| Basis | Homolographic Projection | Orthographic Projection |
| Meaning | A projection in which the network of latitudes and longitudes is developed in such a way that every graticule on the map is equal in area to the corresponding graticule on the globe. It is also known as the equal-area projection. | A projection in which the correct shape of a given area of the earth’s surface is preserved. |
Question (iii). Normal and oblique projections
Answer:
| Basis | Normal Projection | Oblique Projection |
| Meaning | If the developable surface touches the globe at the equator, it is called the equatorial or normal projection. | If projection is tangential to a point between the pole and the equator, it is called the oblique projection. |
Question (iv). Parallels of latitude and meridians of longitude
Answer:
| Basis | Meridians of Longitude | Parallels of Latitude |
| Meaning | The meridians of longitude refer to the angular distance, in degrees, minutes, and seconds, of a point east or west of the Prime (Greenwich) Meridian. | The parallels of latitude refer to the angular distance, in degrees, minutes and seconds of a point north or south of the Equator. |
| Name | Lines of longitude are often referred to as meridians. | Lines oflatitude are often referred to as parallels. |
| Reference point | 0° longitude is called prime meridian. | 0° latitude is called equator. |
| Division | It divides the earth into eastern hemisphere and western hemisphere. | It divides the earth into northern hemisphere and southern hemisphere. |
| Number | These are 360 in number: 180 in the eastern hemisphere and 180 in the western hemisphere. | These are 180 in number: 90 in southern hemisphere and 90 in northern hemisphere. |
| Importance | It helps to determine time of a place. | It helps to determine temperature of a place. |
| Equality | These are not equal. | These are equal. |
Answer the following questions in not more than 125 words
Question (i). Discuss the criteria used for classifying map projection and state the major characteristics of each type of projection.
Answer: Types of Map Projection:
1. On the basis of drawing techniques, map Projections maybe classified perspective, non-perspective and conventional or mathematical. Perspective projections can be drawn taking the help of a source of light by projecting the image of a network of parallels and meridians of a globe on developable surface. Non¬perspective projections are developed without the help of a source of light or casting shadow on surfaces, which can be flattened. Mathematical or conventional projections are those, which are derived by mathematical computation and formulae and have little relations with the projected image.
2. On the basis of developable surface, it can be developable surface and non developable surface. A developable surface is one, which can be flattened, and on which, a network of latitude and longitude can be projected. A globe or spherical surface has the property of non-developable surface whereas a cylinder, a cone and a plane have the property of developable surface. On the basis of nature of developable surface, the projections are classified as cylindrical, conical and zenithal projections.
3. On the basis of global properties, projections are classified into equal area, orthomorphic, azimuthal and equidistant projections.
4. On the basis of location of source of light, projections maybe classified as gnomonic, stereographic and orthographic.
The correctness of area, shape, direction and distances are the four major global properties to be preserved in a map. But none of the projections can maintain all these properties simultaneously. Therefore, according to specific need, a projection can be drawn so that the desired quality may be retained.
Question (ii). Which map projection is very useful for navigational purposes? Explain the properties and limitations of this projection.
Answer: Mercator’s Projection is very useful for navigational purposes. A Dutch cartographer Mercator Gerardus Karmer developed this projection in 1569. The projection is based on mathematical formulae.
Properties:
- It is an orthomorphic projection in which the correct shape is maintained.
- The distance between parallels increases towards the pole.
- Like cylindrical projection, the parallels and meridians intersect each other at right angle. It has the characteristics of showing correct directions.
- A straight line joining any two points on this projection gives a constant bearing, which is called a Laxodrome or Rhumb line.
- All parallels and meridians are straight lines and they intersect each other at right angles.
- All parallels have the same length which is equal to the length of equator.
- All meridians have the same length and equal spacing. But they are longer than the corresponding meridian on the globe.
- Spacing between parallels increases towards the pole.
- Scale along the equator is correct as it is equal to the length of the equator on the globe; but other parallels are longer than the corresponding parallel on the globe; hence the scale is not correct along them.
- Shape of the area is maintained, but at the higher latitudes distortion takes place.
- The shape of small countries near the equator is truly preserved while it increases towards poles.
- It is an azimuthal projection.
- This is an orthomorphic projection as scale along the meridian is equal to the scale along the parallel.
Limitations
- There is greater exaggeration of scale along the parallels and meridians in high latitudes. As a result, size of the countries near the pole is highly exaggerated.
- Poles in this projection cannot be shown as 90° parallel and meridian touching them are infinite.
Question (iii). Discuss the main properties of conical projection with one standard parallel and describe its major limitations.
Answer: A conical projection is one, which is drawn by projecting the image of the graticule of a globe on a developable cone, which touches the globe along a parallel of latitude called the standard parallel. As the cone touches the globe located along AB, the position of this parallel on the globe coinciding with that on the cone is taken as the standard parallel.
Properties
- All the parallels are arcs of concentric circle and are equally spaced.
- All meridians are straight lines merging at the pole. The meridians intersect the parallels at right angles.
- The scale along all meridians is true.
- An arc of a circle represents the pole.
- The scale is true along the standard parallel but exaggerated away from the standard parallel.
- Meridians become closer to each other towards the pole.
- This projection is neither equal area nor orthomorphic.
Limitations
- It is not suitable for a world map due to extreme distortions in the hemisphere opposite the one in which the standard parallel is selected.
- Even within the hemisphere, it is not suitable for representing larger areas as the distortion along the pole and near the equator is larger.
Uses
- This projection is commonly used for showing areas of mid-latitudes with limited latitudinal and larger longitudinal extent.
- A long narrow strip of land running parallel to the standard parallel and having east-west stretch is correctly shown on this projection.
- Direction along standard parallel is used to show railways, roads, narrow river valleys and international boundaries.
- This projection is suitable for showing the Canadian Pacific Railways, Trans- Siberian Railways, international boundaries between USA and Canada and the Narmada Valley.
Activity
1. Construct graticule for an area stretching between 30° N to 70° N and 40° E to 30° W on a simple conical projection with one standard parallel with a scale of 1 : 200,000,000 and interval at an 10° apart.
Answer: Attempt yourself.
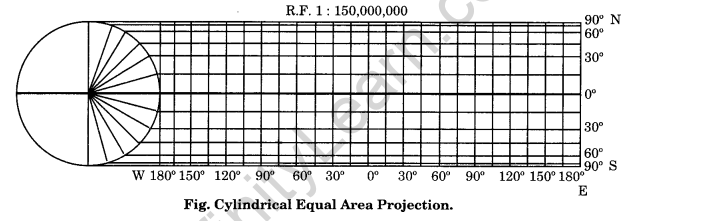
2. Prepare graticule for a Cylindrical Equal Area Projection for the world when R.F. is 1: 150,000,000 and the interval is 15° apart.
Answer:
Construction
Radius of reduced earth:
\(\frac{6,40,000,000}{150,000,000}\)
=4.26cm (round off to 4.3 cm)
Draw a circle of 4.3 cm radius;
Mark the angles of 15°, 30°, 45°, 60°, 75° and 90° for both, northern and southern hemispheres;
Length of the equator = 2π r
=2 × \(\frac{22}{7}\) × 4.3 = 27.03 cm,
Draw a line of 27.03 cm.
Divide it into 24 equal parts at a distance of 1.1262 cm apart.
This line represents the equator;
Draw a line perpendicular to the equator at the point where 0° is meeting the circumference of the circle;
Extend all the parallels equal to the length of the equator from the perpendicular line; and complete the projection as shown in figure given below:
3. Draw a Mercator Projection for the world map when the R.F. is 1:400,000,000 and the interval between the latitude and longitude is 20°.
Answer:
Calculation
\(\frac{250,000,000}{400,000,000}\)=0.625
Radius of the reduced earth R is 0.625″ is 1: 400,000,000
Length of the equator 2πR or
2 × \(\frac{22}{7}\) × 0.625
= 3.93″ inches
Interval along equator
\(\frac { 3.93\times 20 }{ 360 } \) =0.218
Construction
- Draw a line of 3.93″ inches representing the equator as Equation.
- Divide it into 24 equal parts. Determine the length of each division using the following formula: Length of the equator multiplied by interval divided by 360°.
- Calculate the distance for latitude with the help of the table given below:
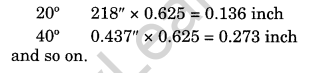
Complete the projection as shown in Figure given below:

NCERT Extra Questions
Question 1. Who had developed Mercator projection?
(a) Mercator Gerardus Karmer
(b) Lambert
(c) Plato
(d) Hambolt
Answer: (a) Mercator Gerardus Karmer
Question 2. Which of the following geographical feature is not there in a map?
(a) Area
(b) Direction
(c) Shape
(d) Topography
Answer: (d) Topography
Question 3. Which of the following is called equal-area projection?
(a) Orthomorphic Projection
(b) Azimuthal Projection
(c) Equidistant projections
(d) Homolographic projection
Answer: (d) Homolographic projection
Question 4. Which projection is obtained by putting the light at the centre of the globe?
(a) Gnomonic Projection
(b) Azimuthal Projection
(c) Equidistant projections
(d) Homolographic projection
Answer: (a) Gnomonic Projection
Question 5. In which projection different parts of the . earth are shown accurately?
(а) Orthomorphic Projection
(b) Azimuthal Projection
(c) Equidistant projections
(d) Homolographic projection
Answer: (d) Homolographic projection
Question 6. Which of the following projection is not classified on the basis of source of light?
(a) Gnomonic Projection
(b) Stereographic Projection
(c) Equal area projection
(d) Orthographic Projection
Answer: (c) Equal area projection
Question 7. Which of the following is not a quality of globe?
(a) Accurate shape of a region
(b) Accurate area of a place
(c) Showing direction of one pace from another place
(d) Showing light
Answer: (d) Showing light
Question 8. Which of the following is not a developable surface?
(a) Angle
(b) Cylindrical
(c) Plane
(d) Map
Answer: (d) Map
Question 9. Which of the following does not have qualities of developable surface?
(a) Conical
(b) Cylindrical
(c) Plane
(d) Globe
Answer: (d) Globe
Viva Questions
Question 1. What is other name for cylindrical equal-area projection?
Answer: The cylindrical equal-area projection is also known as Lambert’s projection.
Question 2. What is Lexodrome or Rhumb Line?
Answer: It is a straight line drawn on Mercator’s projection joining any two points having a constant bearing. It is very useful in determining the directions during navigation.
Question 3. Which map projection is very useful for navigational purposes? Who developed it and on what is it based?
Answer: Mercator’s Projection is very useful for navigational purposes. A Dutch cartographer Mercator Gerardus Karmer developed this projection in 1569. The projection is based on mathematical formulae.
Question 4. Name different types of projections on the basis of method of construction.
Answer: On the basis of method of construction, projections are generally classified into perspective, non-perspective and conventional or mathematical.
Question 5. Name some developable surface.
Answer: A cylinder, a cone and a plane have the property of developable surface.
Question 6. What is mathematical or conventional projection?
Answer: Mathematical or conventional projections are those, which are derived by mathematical computation and formulae and have little relations with the projected image.
Question 7. what is the need of map projection?
Answer: The need for a map projection mainly arises to have a detailed study of a region, which is not possible to do from a globe. Similarly, it is not easy to compare two natural regions on a globe. Therefore, drawing accurate large-scale maps on a flat paper is required.
| Related Links | |
| NCERT Solutions for Class 11 Maths | NCERT Solutions for Class 11 Biology |
| NCERT Solutions for Class 11 Physics | NCERT Solutions for Class 11 Chemistry |
Map Projections Notes
- 1. The need for a map projection mainly arises to have a detailed study of a region, which is not possible to do from a globe. Similarly, it is not easy to compare two natural regions on a globe. Therefore, drawing accurate large-scale maps on a flat paper is required.
- 2. Map projection is the method of transferring the graticule of latitude and longitude on a plane surface. It can also be defined as the transformation of spherical network of parallels and meridians on a plane surface.
Types of Map Projection.
| On the basis of developable surface:
(а) Developable surface (i) Cone (ii) Cylinder (iii) Plane (b) Non- developable surface |
On the basis of drawing techniques:
(a) Perspective (b) Non-Perspective (c) Mathematical and conventional |
On the basis of source of light
(a) Gnomonic, (b) Stereographic (c) Orthograp >On the basis of method of construction (a) Homolographic Projection (b) Orthomorphic Projection |
On the basis of place of touching the surface of the globe:
(a) Equatorial Projection (b) Oblique Projection (c) Polar Projection |
- On the basis of drawing techniques, map Projections may be classified perspective, non-perspective and conventional or mathematical.
- Perspective projections can be drawn taking the help of a source of light by projecting the image of a network of parallels and meridians of a globe on developable surface. Non-perspective projections are developed without the help of a source of light or casting shadow on surfaces, which can be flattened. Mathematical or conventional projections are those, which are derived by mathematical computation and formulae and have little relations with the projected image.
- A developable surface is one, which can be flattened, and on which, a network of latitude and longitude can be projected.
- A globe or spherical surface has the property of non-developable surface whereas a cylinder, a cone and a plane have the property of developable surface.
- On the basis of nature of developable surface, the projections are classified as cylindrical, conical and zenithal projections.
- Cylindrical projections are made through the use of cylindrical developable surface. A paper- made cylinder covers the globe, and the parallels and meridians are projected on it. When the cylinder is cut open, it provides a cylindrical projection on the plane sheet. A Conical projection is drawn by wrapping a cone round the globe and the shadow of graticule network is projected on it. When the cone is cut open, a projection is obtained on a flat sheet.
- Zenithal projection is directly obtained on a plane surface when plane touches the globe at a point and the graticule is projected on it. Generally, the plane is so placed on the globe that it touches the globe at one of the poles.
- The correctness of area, shape, direction and distances are the four major global properties to be preserved in a map. But none of the projections can maintain all these properties simultaneously. Therefore, according to specific need, a projection can be drawn so that the desired quality may be retained.
- On the basis of global properties, projections are classified into equal area, orthomorphic, azimuthal and equidistant projections.
- On the basis of location of source of light, projections may be classified as gnomonic, stereographic and orthographic.
- A Dutch cartographer Mercator Gerardus Karmer developed a projection called Mercator’s Projection in 1569. The projection is based on mathematical formulae. So, it is an orthomorphic projection in which the correct shape is maintained. The distance between parallels increases towards the pole. Like cylindrical projection, the parallels and meridians intersect each other at right angle. It has the characteristics of showing correct directions. A straight line joining any two points on this projection gives a constant bearing, which is called a Laxodrome or Rhumb line.
- The cylindrical equal area projection, also known as the Lambert’s projection, has been derived by projecting the surface of the globe with parallel rays on a cylinder touching it at the equator. Both the parallels and meridians are projected as straight lines intersecting one another at right angles. The pole is shown with a parallel equal to the equator; hence, the shape of the area gets highly distorted at the higher latitude.
Map Projections Important Terms
- Map Projection: It is the system of transformation of the spherical surface onto a plane surface. It is carried out by an orderly and systematic representation of the parallels of latitude and the meridians of longitude of the spherical earth or part of it on a plane surface on a conveniently chosen scale.
- Graticule: The horizontal lines represent the parallels of latitude and the vertical lines represent the meridians of the longitude. The network of parallels and meridians is called graticule.
- Projection: Drawing of the graticule on a flat surface is called projection.
- Lexodrome or Rhumb Line: It is a straight line drawn on Mercator’s projection joining any two points having a constant bearing. It is very useful in determining the directions during navigation.
- The Great Circle: It represents the shortest route between two points, which is often used both in air and ocean navigation.
- Homolographic Projection: A projection in which the network of latitudes and longitudes is developed in such a way that every graticule on the map is equal in area to the corresponding graticule on the globe. It is also known as the equal-area projection.
- Orthomorphic Projection: A projection in which the correct shape of a given area of the earth’s surface is preserved.
- Reduced Earth: A model of the earth is represented by the help of a reduced scale on a flat sheet of paper. This model is called the “reduced earth”.
- Perspective Projections: These can be drawn taking the help of a source of light by projecting the image of a network of parallels and meridians of a globe on developable surface.
- Non-perspective Projections: These are developed without the help of a source of light or casting shadow on surfaces, which can be flattened.
- Mathematical or Conventional Projections: These are those, which are derived by mathematical computation, and formulae and have little relations with the projected image.
- Normal Projection: If the developable surface touches the globe at the equator, it is called the equatorial or normal projection.
- Oblique Projection: If the projection is tangential to a point between the pole and the equator, it is called the oblique projection;
- Polar Projection: If the projection is tangential to the pole, it is called the polar projection.
- Azimuthal or True-Bearing Projection: It is one on which the direction of all points from the centre is correctly represented.
- Equidistant or True Scale Projection: It is that where the distance or scale is correctly maintained.
- Gnomonic Projection: It is obtained by putting the light at the centre of the globe.
- Stereographic Projection: It is drawn when the source of light is placed at the periphery of the globe at a point diametrically opposite to the point at which the plane surface touches the globe.
- Orthographic Projection: It is drawn when the source of light is placed at infinity from the globe, opposite to the point at which the plane surface touches the globe.









