Table of Contents
The a² + b² formula and its counterpart a² – b² constitute fundamental algebraic expressions that hold significant importance in mathematics. These formulas are widely taught and applied starting from the 10th grade and continue to play a crucial role in various educational settings, competitive exams, and real-world problem-solving scenarios.
The a² + b² formula represents the sum of squares of two variables a and b, while a² – b² signifies the difference of squares. These expressions find applications in geometry, trigonometry, physics, engineering, statistics, and even complex number calculations. Mastering these basic algebraic formulas equips individuals with powerful tools to tackle mathematical challenges easily and efficiently.
a2 b2 Formula a²+b²
Let us consider that a and b are two mathematical variables that denote 2 terms of algebra. When you add the square of both algebraic terms, it will be written as a²+b². It expresses a binomial algebraic equation.
The expression a² + b² represents a binomial algebraic equation with ‘a’ and ‘b’ as variables denoting two terms in algebra. When the squares of the respective terms are added, it will be written as a2 + b2.
Derivation of a²+b²
As we all know, (a+b)2 = a2+b2+2ab
a2+b2 = (a+b)2 – 2ab
Also, we know that (a-b)v2 = a2+b2-2ab
a2+b2 = (a-b)2 + 2ab
So, formulas related to a²+b² derived above are concluded below as,
- a² + b² = (a +b)² – 2ab
- a² + b² = (a -b)² + 2ab
This fundamental formula a² + b² finds wide applications in various disciplines. Geometrically, it corresponds to the Pythagorean theorem, which is crucial in proving geometric relationships and trigonometric identities. a² + b² calculates magnitudes, distances, and forces in physics and engineering, essential in mechanics, electricity, and waves. Statistics determines variances and standard deviations, providing insights into data dispersion. The formula is also pertinent in working with complex numbers, employed in modulus and absolute value representation and linked to Euler’s formula. Its versatility and significance make it a cornerstone in mathematics and practical applications.
a2 b2 Formula a²-b²
The expression a² – b² represents a binomial algebraic equation, where ‘a’ and ‘b’ are mathematical variables signifying two terms in algebra.
1. Sum of Squares Formula (a2+b2a^2 + b^2):
The sum of squares formula expresses the sum of the squares of two terms. It can be derived from the square of a binomial:
(a+b)2=a2+2ab+b2(a + b)^2 = a^2 + 2ab + b^2
Rearranging this equation gives:
a2+b2=(a+b)2−2aba^2 + b^2 = (a + b)^2 – 2ab
Alternatively, using the square of the difference:
(a−b)2=a2−2ab+b2(a – b)^2 = a^2 – 2ab + b^2
Rearranging this yields:
a2+b2=(a−b)2+2aba^2 + b^2 = (a – b)^2 + 2ab
These identities are useful for simplifying expressions involving the sum of squares.
2. Difference of Squares Formula (a2−b2a^2 – b^2):
The difference of squares formula states that the difference between the squares of two terms equals the product of their sum and difference:
a2−b2=(a+b)(a−b)a^2 – b^2 = (a + b)(a – b)
Proof:
Starting with the right-hand side:
(a+b)(a−b)=a(a−b)+b(a−b)=a2−ab+ab−b2=a2−b2(a + b)(a – b) = a(a – b) + b(a – b) = a^2 – ab + ab – b^2 = a^2 – b^2
This identity is particularly useful for factoring expressions where one term is subtracted from another squared term.
Applications:
- Simplifying Expressions: Both formulas are instrumental in breaking down complex algebraic expressions into more manageable factors.
- Solving Equations: They aid in solving quadratic equations and other polynomial equations by factoring.
- Geometry: The sum of squares formula is foundational in the Pythagorean theorem, which relates the sides of a right-angled triangle:
a2+b2=c2a^2 + b^2 = c^2
Derivation of a2 b2
The a² – b² formula can be derived geometrically using subtracting the area of a small square from a larger square. This geometric representation helps us understand how the difference of squares can be factored into the product of (a + b) and (a – b). The area of the subtracted shape, a square of side b, is equal to a² – b². By rearranging the shape and forming a rectangle with sides (a + b) and (a – b), we can observe that the area of the rectangle is also equal to a² – b².
Thus, we arrive at the factorisation a² – b² = (a + b)(a – b).
This fundamental formula holds significant importance across various mathematical disciplines and practical applications. Geometrically, it relates to the difference of squares, facilitating polynomial factorisation and special geometric shapes analysis. In trigonometry, a² – b² is instrumental in deriving identities and solving complex equations involving sines, cosines, and tangents. The formula finds applications in mechanics, optics, and electrical circuits in physics and engineering, contributing to the derivation of crucial equations. Understanding and applying a² – b² empower professionals to tackle intricate problems efficiently, making notable advancements in their respective fields.
Step-by-Step Derivation
-
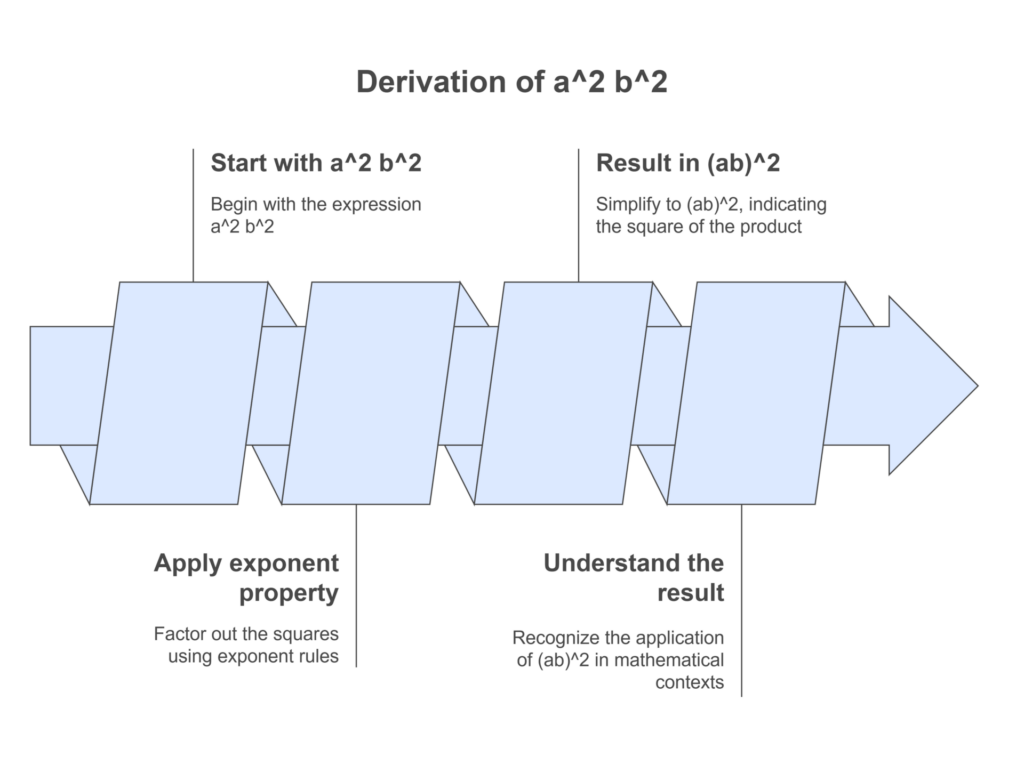
Start with the expression: [ a^2 b^2 ]
-
Apply the property of exponents: We can factor out the squares: [ a^2 b^2 = (ab)^2 ]
-
Understanding the result: The expression ( (ab)^2 ) indicates that we are squaring the product of ( a ) and ( b ). This can be useful in various mathematical contexts, such as simplifying equations or solving problems involving products of variables.
a2 b2 Formula: Examples
Question: using the sum of squares formula, calculate the value of (2)² + ()03².
Solution:
Given that the value of a = 2, b = 3
By using the a² + b² Formula,
a² + b² =(a +b)² – 2ab
= (2 + 3)² – 2 (2)(3)
= 5² – 2 (6)
= 25 – 12
= 13
Therefore, a² + b² = 13
Question: Using the formula of the square, find the value of the given expression 2² – 3².
Solution:
Given that the value of a = 2, b = 3
By using the formula of the square,
a² + b² = (a + b)² − 2ab
= (2 + 3)(2 – 3)
= (5)(-1)
= -5
Therefore, a² – b² = -5
Verification of a2 – b2 Formula
Let’s verify the identity of the a2−b2a^2 – b^2 formula step by step.
Formula: a2−b2=(a+b)(a−b)a^2 – b^2 = (a + b)(a – b)
Verification (Algebraic Method):
Take the right-hand side:
(a+b)(a−b)(a + b)(a – b)
Use the distributive property (also known as FOIL for binomials):
=a(a−b)+b(a−b)= a(a – b) + b(a – b)=a2−ab+ab−b2= a^2 – ab + ab – b^2
Now, simplify:
a2−ab+ab−b2=a2−b2a^2 – ab + ab – b^2 = a^2 – b^2
LHS = RHS, hence verified.
Verification (Example with Numbers):
Let’s take:
- a=7a = 7
- b=3b = 3
Now compute both sides of the equation.
Left Side:
a2−b2=72−32=49−9=40a^2 – b^2 = 7^2 – 3^2 = 49 – 9 = 40
Right Side:
(a+b)(a−b)=(7+3)(7−3)=10×4=40(a + b)(a – b) = (7 + 3)(7 – 3) = 10 × 4 = 40
Both sides match. Verified again!
FAQs on a2 b2 Formula
What is the a2 + b2 formula used for in real-life applications?
The a2 + b2 formula is utilized in various fields such as geometry, trigonometry, physics, engineering, and statistics. It aids in calculating magnitudes, distances, and forces, and is fundamental in deriving equations related to complex numbers.
How is the a2 + b2 formula derived geometrically?
Geometrically, the a2 + b2 formula can be visualized by considering the area of a square with side length a + b Subtracting the areas of the smaller squares with side lengths a and b from this larger square leads to the expression a2 + b2.
What does the a2 – b2 formula represent, and how is it derived?
The a2 – b2 formula represents the difference of squares and is derived from the identity (a + b)(a – b) = a2 – b2. This identity is useful for factoring expressions where one term is subtracted from another squared term.
What are some real-life applications of the a2 – b2 formula?
The a2 – b2 formula is applied in various scenarios, such as simplifying expressions in engineering calculations, optimizing algorithms in computer science, and solving problems in physics related to kinematics and dynamics.









