Table of Contents
To understand the Inverse of Matrices, one initially needs to understand Matrices.
A matrix is a rectangular array of numbers, symbols, or expressions arranged in rows and columns. It is a fundamental mathematical concept used in various fields, including linear algebra, computer science, physics, and engineering.
In matrix notation, a matrix is typically represented by a capital letter and enclosed in brackets or parentheses. The size of a matrix is determined by the number of rows and columns it contains. For example, an “m x n” matrix has m rows and n columns.
Inverse of a Matrix
The inverse of matrix is obtained by dividing the adjoint of the given matrix by the determinant of the given matrix. Students must note that matrix inverse could be found only for square matrices.
This article discusses about the inverse of a matrix, steps to find the inverse of a matrix, the properties of the inverse matrix along with the examples.
Matrix Inverse
If A is a non-singular square matrix, then there exists a n x n matrix A-1 which is called the inverse matrix of A, such that it satisfies the property:
AA-1 = A-1A = I, where I is the Identity matrix.
The identity matrix for the 2 x 2 matrix is given by:
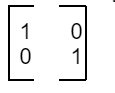
It is noted that to find the inverse of a matrix, the square matrix should be a non-singular matrix whose determinant value is not equal to zero.
Let us take the square matrix A
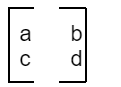
Where a, b, c, and d are the numbers.
- The determinant of matrix A is written as ad-bc.
- For the existence of the inverse of the matrices, the determinant should not equal zero.
- The inverse matrix can be found for 2× 2, 3× 3, …n × n matrices.
- As the value of n increases, finding the inverse of the matrix becomes difficult.
Inverse Matrix Method
The inverse of a matrix can be found using three different methods. However, any of these three methods will produce the same result.
Method 1: Inverse-matrix-method
Let the matrix A be:
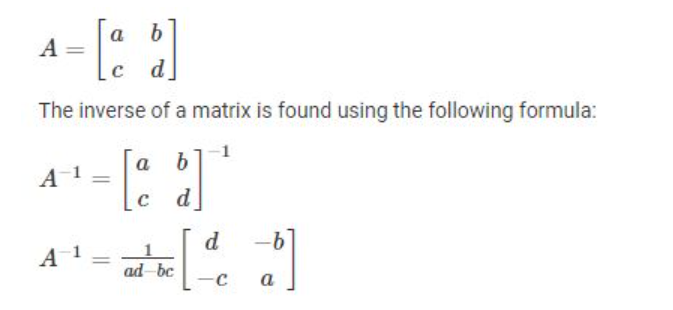
We can find the inverse of a matrix using this method.
Method 2: minors and cofactors methods
Second method of finding the matrix inverse is by using the minors and cofactors of elements of the given matrix.
The inverse matrix can be found using the following equation:
A-1 = adj(A)/det(A),
where adj(A) refers to the adjoint of a matrix A,
And det(A) refers to the determinant of a matrix A.
To know more about the adjoint and co-factor of a matrix,
Check :
- Adjoint of a matrix A
- Cofactor of a matrix A
Method 3: Elementary Transformation
To find an Inverse of a Matrix by Elementary Transformation we follow the below-mentioned method.
Let us consider three matrices X, A and B such that X = AB.
To find the inverse of a matrix using elementary transformation, we convert the given matrix into an identity matrix.
Check: how to do elementary transformations of matrices
If, for a matrix A, A-1 exists, then to determine A-1 using elementary row operations, we follow the following steps.
- Let A = IA, where I is the identity matrix of the same order as A.
- Apply a sequence of row operations on LHS and RHS till we get an identity matrix on the LHS. while performing the operations we will get I = BA. The matrix B obtained on the RHS is the inverse of matrix A.
- To find the inverse of A using column operations, write A = IA and apply column operations in a similar manner as the above-mentioned step sequentially till I = AB is obtained, where B is the inverse matrix of A.
Also check: how to find the inverse of a matrix using elementary operations
Inverse Matrix 2 x 2 Example
To understand in a better way, let us take a look at the following example.

Properties of the inverse of a matrix
A few important properties of the inverse matrix are mentioned below.
- If matrix A is nonsingular, then (A-1)-1 = A
- If A and B are nonsingular matrices, then AB is also nonsingular.
Thus, (AB)-1 = B-1A-1 - If A is nonsingular matrix, then (AT)-1 = (A-1)T
- If A is any matrix and A-1 is its inverse, then AA-1 = In = A-1A , where n is the order of matrices
FAQs on Inverse of Matrices
What is concept inverse of a matrix?
Matrices also have reciprocals just like numbers. In the case of matrices, this reciprocal is called an inverse matrix. If A is a square matrix and B is its inverse, then the product of matrices A and B is equal to the unit matrix.
How do you find the inverse of a 3×3 matrix?
The steps required to find the inverse of a 3×3 matrix are:
Compute the determinant of the given matrix and check whether the matrix is invertible.
Calculate the determinant of 2×2 minor matrices.
Formulate the matrix of cofactors.
Take the transpose of the cofactor matrix to get the adjugate matrix.
Finally, divide each term of the adjugate matrix by the determinant
Is adjoint and inverse the same?
No, the adjoint matrix and inverse matrix are not the same. However, by dividing the each term of the adjoint of the matrix by the determinant of the original matrix, we get an inverse matrix.
How to do you know whether the given matrix has an inverse?
If the determinant of a given matrix is not equal to 0, i.e. it is non-singular, then the matrix is invertible.








