Table of Contents
Introduction to Pythagorean triples
Pythagorean triples, denoted by (a, b, c), play a significant role in mathematics, particularly in geometry. These triples are sets of three positive integers that satisfy the fundamental Pythagorean theorem, which states that in a right-angled triangle, the sum of the squares of the lengths of the two shorter sides (a and b) is equal to the square of the length of the longest side, the hypotenuse (c).
Mathematically, it can be expressed as a2 + b2 = c2.
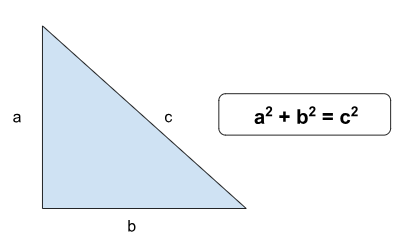
In a right-angled triangle, the side ‘c’ represents the hypotenuse, opposite to the right angle, while the sides ‘a’ and ‘b’ correspond to the perpendicular and base, respectively. The well-known and simplest Pythagorean triple is (3, 4, 5), where 32 + 42 = 52
Pythagorean triples can be traced back to the ancient Greek mathematician Pythagoras, who lived around 570 BC. Pythagoras made groundbreaking contributions to various fields, such as mathematics, science, and philosophy. His fascination with triangles containing right angles led to the discovery of the Pythagorean theorem, a fundamental geometric principle that remains widely studied and applied today.
What are Pythagorean Triples?
Pythagorean triples are comprised of three positive integers that satisfy the Pythagorean Theorem.
For instance, consider the classic Pythagorean triple (3, 4, 5).
By evaluating the equation, we find that 32 + 42 equals 52, which is 9 + 16 = 25. Hence, the triplet (3, 4, 5) perfectly adheres to the Pythagorean Theorem.
Pythagoras Triples Table
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (36, 77, 85) | (65, 72, 97) |
Pythagoras Triples Formula
Expressed as p2 + q2 = r2, this fundamental theorem has diverse applications in geometry and trigonometry, enabling the calculation of unknown side lengths in right-angled triangles.
How to Form Pythagorean Triples?
Example: For x = 7
(x2/2) – 0.5 = (49/2) – 0.5 = 24.5 – 0.5 = 24
(x2/2) + 0.5 = (49/2) + 0.5 = 24.5 + 0.5 = 25
Pythagorean triple: (7, 24, 25)
Let the number be “x.”
The Pythagorean triple is: x, (x/2)2 – 1, (x/2)2 + 1.
Example: For x = 16
(x/2)2 – 1 = (16/2)2 – 1 = 82 – 1 = 63
(x/2)2 + 1 = (16/2)2 + 1 = 82 + 1 = 65
Pythagorean triple: (16, 63, 65)
Pythagorean Triples Problems
Let’s check if (9, 40, 41) satisfies the Pythagorean Theorem.
(a, b, c) = (9, 40, 41)
The Pythagorean Theorem is given by a2 + b2 = c2
Now, plug in the values:
92 + 402 = 412
81 + 1600 = 1681
1681 = 1681
Since the sum of the squares of the two shorter sides (9 and 40) equals the square of the longest side (41), the given set of integers (9, 40, 41) satisfies the Pythagorean Theorem. Therefore, (9, 40, 41) is indeed a Pythagorean triple.
Let’s apply the Pythagorean Theorem to (10, 21, 29).
(a, b, c) = (10, 21, 29)
Using the Pythagorean Theorem formula, we have:
102 + 212 = 292
100 + 441 = 841
541 ≠ 841
FAQs on Pythagorean Triples
Is 28, 21, and 35 a Pythagorean triplet?
Yes, to check, we apply the Pythagorean Theorem:
282 + 212 = 784 + 441 = 1225
352 = 1225 Since 28, 21, and 35 satisfy the equation a2 + b2 = c2, they form a Pythagorean triplet.
Which of the following are Pythagorean triplets?<br /> a) (9, 40, 41)<br /> b) (8, 15, 18)<br /> c) (7, 24, 25)
Applying the Pythagorean Theorem:
a) 92 + 402 = 1681 ≠ 412 (Not a Pythagorean triplet) b) 82 + 152 = 289 = 172 (Pythagorean triplet)
c) 72 + 242 = 625 = 252 (Pythagorean triplet) The Pythagorean triplets are (8, 15, 18) and (7, 24, 25).
Which of the following is not a Pythagorean triplet among the following sets:a) (9, 40, 41) b) (8, 15, 18) c) (7, 24, 25)
The set (9, 40, 41) is not a Pythagorean triplet since 92 + 402 ≠ 412.








