Table of Contents
Introduction to rank of a matrix
Matrices are basic mathematical objects that are used in many domains, including linear algebra, computer science, physics, and engineering. The rank of a matrix is an important notion in linear algebra since it offers information about the properties and behaviour of matrices. In this article, we will look at what a matrix’s rank is, how to calculate it, its features, and present solved cases to demonstrate its use..
What is rank of a matrix
The maximum number of linearly independent rows or columns in a matrix is referred to as its rank. Simply said, it is the maximum amount of rows or columns that contribute to the overall structure of the matrix. The symbol “rank(A),” which represents the given matrix, signifies the rank of a matrix..
How to find the rank of a matrix
A matrix’s rank can be determined using a variety of approaches, including:
Reduced Row-Echelon Form or Row-Echelon Form
The number of non-zero rows or pivot elements acquired by conducting row operations to transform the matrix into row-echelon form or reduced row-echelon form corresponds to the matrix’s rank.
Determinants
The rank can be determined by analysing the determinants of submatrices. The rank equals the highest order of any non-zero determinant derived from the submatrices.
SVD (Singular Value Decomposition)
The rank can be determined using SVD, a sophisticated matrix decomposition technique. Counting the number of non-zero singular values received from the decomposition yields the rank.
Properties of rank of a matrix
A matrix’s rank has several key properties:
- A matrix’s rank is always less than or equal to the sum of its rows and columns.
- A matrix is said to have full rank or be a full-rank matrix if its rank is equal to the number of rows or columns.
- A matrix’s rank is equal to its transpose’s rank, it means
Rank (A) = Rank (AT) - The sum of two matrices A and B has a rank that is less than or equal to the sum of their individual rankings It means
Rank (A + B) ≤ Rank (A) + Rank(B)
Solved examples on rank of a matrix
Find the rank of a matrix
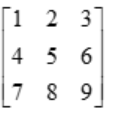
Solution: Reduce the given matrix in Echlon form as below

Change the second and third rows as R2 → R2 – 4R1 and R3 → R3 – 7R1
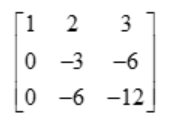
Change the third row as R3 → R3 – 2R2
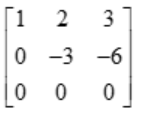
The above matrix is in Echelon form, hence the number of non zero rows is the rank of the matrix.
Hence, the rank of the matrix  is 2
is 2
Find the rank of a matrix
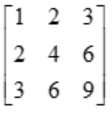
Solution: Reduce the given matrix in Echlon form as below

Change the second and third rows as R2 → R2 – 2R1 and R3 → R3 – 3R1
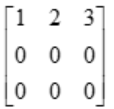
The above matrix is in Echelon form, hence the number of non zero rows is the rank of the matrix.
Hence, the rank of the matrix  is 1
is 1
Frequently asked questions on Rank of a matrix
What is meant by rank of a matrix?
The maximum number of linearly independent rows or columns in a matrix is referred to as its rank. In other words, it reflects the most rows or columns that contribute to the overall structure of the matrix without being redundant or dependent on one another.
What does the rank of a matrix is zero indicates?
A rank of zero denotes that all of the matrix's rows and columns are linearly dependent, resulting in a matrix with no independent information.
Is it feasible to have different ranks for two matrices with the same dimensions?
That is feasible. The rank is determined by the linear independence of the rows and columns, which might differ amongst matrices.
Can a matrix's rank exceed the amount of rows or columns?
No, a matrix's rank is always less than or equal to the sum of its rows and columns.
When is the rank of the matrix is equal to the order of the matrix?
When a matrix is a full-rank matrix, its rank is equal to its order. A full-rank matrix is one with a rank equal to the smallest number of rows and columns. In other words, if a matrix contains m rows and n columns, the rank of the matrix will be equal to m if m n, or n if n m. This indicates that each row or column of the matrix is linearly independent and contributes to the matrix's overall structure.
What are the steps to find the rank of a square matrix of order 3
Step 1: Begin with the given three-dimensional square matrix. Step 2: Use basic row operations to convert the matrix to its row-echelon or reduced row-echelon form. The purpose is to generate a triangular matrix with non-zero leading entries (pivot elements). Step 3: Count the number of non-zero rows or pivot elements in the matrix's row-echelon or reduced row-echelon forms. This number represents the matrix's rank. Step 4: The matrix's rank is determined by counting the number of non-zero rows or pivot elements.









